Wpływ osłony przeciwsłonecznej na współczynnik przenikania ciepła okna
The influence of the sun visor on the window heat transfer coefficient
![RYS. 1. Termogram pokazujący budynek od strony frontowej (południowo‑zachodniej)
rys. [2]](https://www.izolacje.com.pl/media/cache/typical_view/data/202010/oslona-przeciwsloneczna-przenikanie-ciepla.jpg)
RYS. 1. Termogram pokazujący budynek od strony frontowej (południowo‑zachodniej)
rys. [2]
Minimalizowanie zużycia energii na ogrzewanie w budynkach mieszkalnych uzyskiwane jest zazwyczaj dzięki stosowaniu najnowszych technologii izolacji termicznej. Bardzo często związane jest to ze wzrostem zapotrzebowania na energię do chłodzenia pomieszczeń. Nierzadko zatem na równi stawiane jest zapewnienie temperatury komfortu cieplnego budynków zimą oraz ochrona pomieszczeń przed przegrzewaniem w okresie letnim.
Zobacz także
BREVIS S.C. Czy nawiewniki w oknach są obowiązkowe – najważniejsze Informacje

Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu...
Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu uniknięcia negatywnych skutków zbyt dużej wilgotności, to już dyskomfort siedzenia w dusznym i nieprzewietrzonym pomieszczeniu zna każdy. Oprócz wentylacji grawitacyjnej do niedawna odpowiednią cyrkulację powietrza zapewniały nieszczelności w oknach. Jednak rozwój technologiczny i zwiększenie szczelności...
DAKO Jak wybrać drzwi do nowoczesnego domu?

Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie...
Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie aspekty trzeba zwrócić szczególną uwagę, wybierając drzwi zewnętrzne!
Czytaj całość »
RoletyAlu Sp. z o.o. Jak łatwo kupić rolety zewnętrzne przez internet?
Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość...
Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość złożenia zamówienia bezpośrednio u producenta rolet zewnętrznych pozwala wyeliminować pośredników, co skraca czas potrzeby na realizację zamówień i przekłada się na dużo niższe ceny.
Czytaj całość »Ważnym aspektem wpływającym na izolacyjność termiczną stolarki okiennej i stopień przegrzania pomieszczeń są osłony przeciwsłoneczne. Wśród typowych osłon przeciwsłonecznych wymienić można:
- rolety i żaluzje,
- ściany lamelowe,
- łamacze światła,
- osłony czerpnii i in.
W zależności od tego, z jakiego typu osłoną mamy do czynienia i z jakiego materiału jest ona wykonana, a także jakie ma parametry przepuszczalności powietrza, należy wyznaczyć współczynnik przenikania ciepła Uws, który uwzględnia wpływ zastosowanego detalu przeciwsłonecznego w oknie [1].
Zastosowanie osłon przeciwsłonecznych jest szczególnie uzasadnione przede wszystkim wtedy, gdy chcemy zmniejszać niepożądane (nadmierne) zyski ciepła oraz jeśli zależy nam na ograniczeniu strat ciepła.
- W okresie letnim ich funkcją jest ograniczenie nagrzewania budynków przez promienie słoneczne, a także minimalizacja refleksu świetlnego, który powstaje w słoneczne dni.
- W przypadku dni pochmurnych ich zadaniem jest umożliwianie maksymalnego dopływu światła widzialnego do wnętrz pomieszczeń.
Wynika z tego, że osłony powinny cechować się zmiennością parametrów dla różnych pór roku, a taki efekt można uzyskać, gdy osłony są ruchome.
![RYS. 1. Termogram pokazujący budynek od strony frontowej (południowo‑zachodniej), zdjęcie wykonane w godz. od 5.30 do 6.30; rys. [2] RYS. 1. Termogram pokazujący budynek od strony frontowej (południowo‑zachodniej), zdjęcie wykonane w godz. od 5.30 do 6.30; rys. [2]](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/b-wplyw-oslony-przeciwslonecznej-rys1.jpg)
RYS. 1. Termogram pokazujący budynek od strony frontowej (południowo‑zachodniej), zdjęcie wykonane w godz. od 5.30 do 6.30; rys. [2]
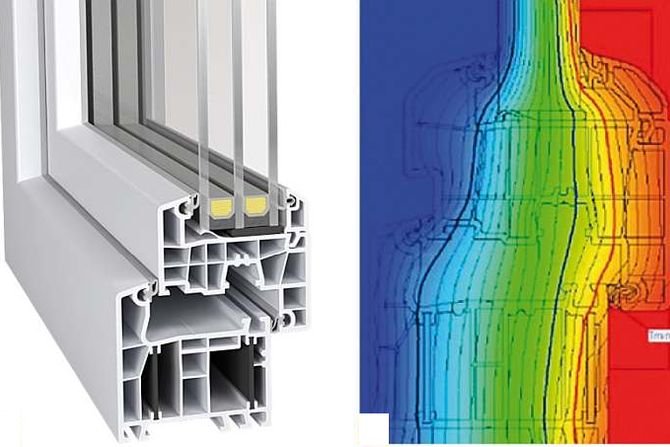
Skuteczność zastosowania zewnętrznych osłon przeciwsłonecznych została przedstawiona na RYS. 1 wg pracy [2]. Pokazano na nim, jak kształtują się temperatury na powierzchniach okien na ścianie frontowej budynku mieszkalnego z zastosowaną osłoną zewnętrzną i bez osłony w identycznych warunkach atmosferycznych. Można dostrzec znaczną różnicę barwy okna lewego względem okna prawego, co oznacza, że temperatura powierzchni okna z zastosowaną osłoną jest niższa niż powierzchni okna bez osłony.
Metoda obliczania współczynnika przenikania ciepła okna z osłoną przeciwsłoneczną
Do obliczenia współczynnika przenikania ciepła okna z uwzględnieniem efektu osłon przeciwsłonecznych Uws zastosowano podejście opisane w pracy [1], według którego osłonę rozpatruje się jako element dodatkowy i uwzględnia się we wzorze w następujący sposób:

gdzie:
Uw - współczynnik przenikania ciepła okna bez uwzględnienia wpływu osłony przeciwsłonecznej, [W/(m2·K)],
ΔR - wartość dodatkowego oporu cieplnego dla osłony przeciwsłonecznej, [(m2·K)/W].
Wartości dodatkowego oporu cieplnego ΔR wynikającego z zastosowania różnych osłon przeciwsłonecznych umieszczonych po zewnętrznej stronie okna przyjmowano zgodnie z normą [3], w zależności od typu i materiału z jakiego jest wykonana osłona oraz jej przepuszczalności powietrza.
Współczynnik przenikania ciepła okna bez uwzględnienia wpływu osłony Uw obliczono metodą składnikową [4]. Metoda ta dzieli fragment przegrody na pola powierzchni o różnych właściwościach cieplnych, a całkowity współczynnik przenikania ciepła oblicza się za pomocą ważonych powierzchniowo wartości U elementów składowych. Według tej metody współczynnik przenikania ciepła Uw pojedynczego jednoskrzydłowego okna można obliczać według wzoru:
 (1)
(1)
gdzie:
Ug, Uf, Umtos - współczynniki przenikania ciepła, odpowiednio: oszklenia, ramy, ramiaków i stojaków ościeżnic,
Ag, Af, Amtos - pole powierzchni, odpowiednio: oszklenia, ramy, stojaków i ramiaków ościeżnic,
Ψg–f - liniowy współczynnik przenikania ciepła mostków termicznych powstających na granicy szyba–rama,
lg–f - długość liniowego mostku termicznego powstającego na styku szyba–rama.
Wartości pól powierzchni Ag, Af, Amtos oraz długość mostka lg–f mogą być określone ze wzorów opracowanych przez autorów:

gdzie:
bo, bskr, bf, bmos, btos - szerokość, odpowiednio: okna, skrzydła, elementów ramy, stojaków i ramiaków ościeżnic,
ho, hskr - wysokość, odpowiednio: okna, skrzydła.
Odnosząc się do przedstawionych wzorów (1-7), autorzy stworzyli algorytm do wyliczania szukanego współczynnika przenikania ciepła okien Uw przy zmianie wartości wybranych czynników ( RYS. 2 ), który stanowił podstawę do opracowania autorskiego programu w Microsoft Excel.

RYS. 2. Schemat blokowy obliczania współczynnika przenikania ciepła Uws okna z osłoną przeciwsłoneczną; rys. archiwum autorów
Opis badanego obiektu
Współczesne technologie montażu stolarki okiennej z PVC pozwalają stosować okna z szerokim zakresem zmienności ich proporcji.
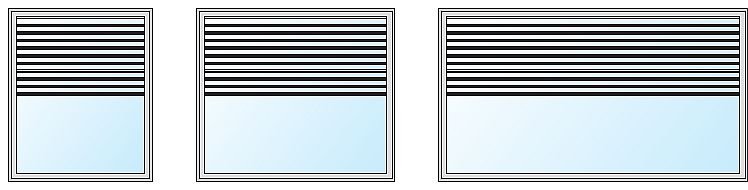
W badaniu, z uwzględnieniem najczęściej stosowanych rozmiarów okien w budynkach mieszkalnych, zostały wybrane warianty stolarki okiennej z powierzchnią od 1,20 m2 do 3,60 m2. Wysokość okien przyjęto jako parametr stały równy 1,48 m.
Schematy badanych wariantów okien podano na RYS. 3.
Dla badanych okien po ich zewnętrznej stronie zgodnie z normą [3] przewidziano osłonę przeciwsłoneczną drewnianą grubości 20 mm w trzech wariantach:
- bardzo wysokiej przepuszczalności (wartość dodatkowego oporu cieplnego ΔR = 0,080 (m2·K)/W),
- średniej przepuszczalności (ΔR = 0,220 (m2·K)/W),
- szczelną (ΔR = 0,360 (m2·K)/W) [5].
Model matematyczny współczynnika przenikania ciepła okna z osłoną przeciwsłoneczną
Zgodnie z przyjętym celem badania jako funkcję celu Y wybrano współczynnik przenikania ciepła okna z osłoną przeciwsłoneczną Uws, [W/(m2·K)].
Przy wyborze czynników na podstawie wstępnej analizy wytypowano najważniejsze z nich wpływające na funkcje Y oraz zapewniające uzyskanie informacji interesującej odbiorców stolarki okiennej. Przeanalizowano również spełnienie podstawowych wymagań stawianych czynnikom: powinny być sterowalne, jednoznaczne, niesprzeczne i wzajemnie niezależne [6].
Po analizie do badania przyjęto zależność współczynnika Uws od następujących czynników:
- wielkości dodatkowego oporu cieplnego dla odpowiedniego typu osłon ΔR (czynnik X1),
- pola powierzchni okna A0(czynnik X2),
- szerokości elementów ramy bf(czynnik X3),
- współczynnika przenikania ciepła oszklenia Ug(czynnik X4),
- współczynnika przenikania ciepła ramy Uf(czynnik X5).
Te czynniki określają wkład w wielkość Uws bezpośrednio poprzez ΔR, Ug, Uf lub pośrednio przez A0, bf.
Przypuszczano, że szukaną zależność Y = ƒ(X1, X2, X3, X4, X5) może opisywać wielomian drugiego stopnia. Do uzyskania danych dla opisu tej zależności przeprowadzono 5-czynnikowy eksperyment obliczeniowy według planu drugiego stopnia ( TABELA ). Zastosowano kompozycyjny symetryczny trójpoziomowy plan zawierający 26 prób [5]. Do wyliczenia wartości Yi w 26 wierszach planu wykorzystano oprogramowanie Microsoft Excel.
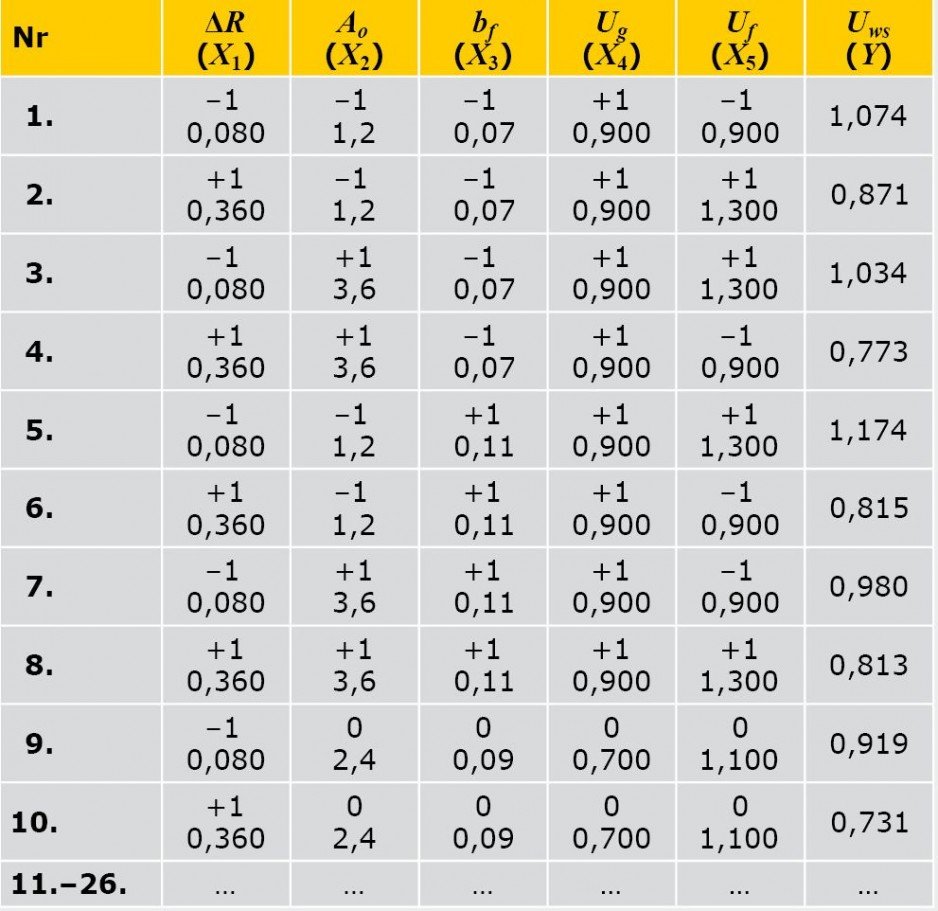
TABELA. Macierz planowania i wyniki eksperymentu obliczeniowego do określenia współczynnika przenikania ciepła Uws okna z osłoną przeciwsłoneczną
Przed rozpoczęciem obliczeń wykonano uzasadniony wybór zakresu zmienności czynników.
- Wielkość dodatkowego oporu cieplnego dla odpowiedniego typu osłon ΔR (czynnik X1):
- na dolnym poziomie przyjęto 0,080 (m2·K)/W;
- jako górny poziom przyjęto wartość 0,360 (m2·K)/W;
- na średnim poziomie ΔR przyjęto 0,220 (m2·K)/W.
Wybrany zakres zmienności odpowiadał wartościom oporów cieplnych dla przytoczonych wyżej wariantów osłony przeciwsłonecznej okien według [5].
- Pole powierzchni okna A0(czynnik X2):
- na dolnym poziomie przyjęto równe 1,20 m2;
- jako górny poziom przyjęto powierzchnię okna trzykrotnie zwiększoną - 3,60 m2;
- odpowiednio na średnim poziomie przyjęto 2,40 m2.
W celu uniknięcia niejednoznaczności tego czynnika wysokość okien przyjęto jako wartość stałą i wynoszącą 1,48 m.
- Szerokość elementów ramy skrzydłowej bf(czynnik X3) przyjęto też na trzech poziomach:
- dolny - 0,07,
- górny - 0,09,
- sredni - 0,11 m. - Współczynnik przenikania ciepła oszklenia Ug(czynnik X4) przyjęto:
- na dolnym poziomie wartość równą 0,50 W/(m2·K);
- na górnym - 0,90 W/(m2·K),
- na średnim - 0,70 W/(m2·K). - Współczynnik przenikania ciepła ramy Uf(czynnik X5):
- na dolnym poziomie wartość równą 0,90 W/(m2·K);
- na górnym - 1,30 W/(m2·K),
- na średnim - 1,10 W/(m2·K);
Pozostałe parametry przyjęto na stałym poziomie:
- szerokość stojaków bm= 0,02 m,
- szerokość ślemii bt= 0,035 m,
- szerokość stojaków i ramiaków ościeżnic bmos= btos= 0,035 m [9].
Pole powierzchni fragmentu ściany osłonowej przyjęto równe 9,72 m2.
Współczynniki przenikania ciepła:
- nieprzezroczystych elementów składowych okna przyjęto na poziomie: Um= Ut= Umtos= 1,10,
- ściany pełnej Uśp = 0,23 W/(m2·K);
- liniowych współczynników przenikania ciepła mostków termicznych:
- na granicy szyba–rama Ψf–g = 0,08,
- na granicy rama–ściana – Ψf–śc = 0,023 W/(m·K).
Wyżej wymienione wartości naturalne czynników Ẋ1, Ẋ2, Ẋ3, Ẋ4, Ẋ5 i odpowiadające im wartości unormowane X1, X2, X3, X4, X5 przedstawiono w TABELI. Według [5] przejście z wartości naturalnych Ẋi do unormowanych Xi wyraża się wzorem:
![]() (8)
(8)
gdzie:
Ẋi, Ẋimax, Ẋimin - odpowiednio bieżące, maksymalne i minimalne wartości naturalne i-tego czynnika.
Na podstawie wyników obliczeń (tabela) za pomocą metody najmniejszych kwadratów [7] opracowano równanie regresji zależności Y = ƒ(X1, X2, X3, X4, X5). Istotność współczynników tego równania oceniono za pomocą t-kryterium.
Metoda testowania współczynników szczegółowo opisana została przez autorów w [8].
W wyniku testu pięć współczynników okazało się nieistotnych. Po ich usunięciu przyjęto postać końcową równania z k + 1 = 16 współczynnikami:
 (9)
(9)
Potwierdzona została również adekwatność uzyskanego modelu według metody, opisanej w [7].
Dany model posiadał:

Dodatkowo jakość aproksymacji danych opracowanym równaniem oceniono według kryterium F [7].
Przy poziomie istotności α = 0,05 i liczbie stopni swobody

okazało się, że wartość obliczeniowa kryterium ![]() wielokrotnie przekracza wartość tabelaryczną F0,05;25;10 = 2,73 [7], co potwierdza jego wysoką jakość.
wielokrotnie przekracza wartość tabelaryczną F0,05;25;10 = 2,73 [7], co potwierdza jego wysoką jakość.
Analiza wyników badania
Za pomocą równania regresji (9) przeanalizowano stopień i charakter wpływu poszczególnych czynników na współczynnik przenikania ciepła Uws okna z osłoną przeciwsłoneczną.
Analizę przeprowadzono dla zmiennych w postaci naturalnej. Autorów interesował przede wszystkim wpływ czynnika X1, czyli dodatkowego oporu cieplnego dla odpowiedniego typu osłon ΔR, wybranego w badaniu jako główny parametr charakteryzujący wpływ osłony przeciwsłonecznej na wielkość współczynnika Uws.
Analizując opracowany model, wykryto, że w centrum Gp przestrzeni czynnikowej, które charakteryzuje się współrzędnymi ΔR = 0,22 (m2·K)/W, Ao= 2,40 m2, bf= 0,09 m, Ug= 0,70, Uf= 1,10 W/(m2·K), wielkość Uws wynosi 0,814 W/(m2·K).
Wykorzystując punkt Gp jako punkt odniesienia, oszacowano wpływ poszczególnych czynników. Okazało się, że korzystny wpływ na wielkość Uws wykazują dwa czynniki: ΔR(X1) oraz A0(X2). Przy zmianie ich wartości od –1 do +1 następuje zmniejszenie współczynnika Uws o 21,8% dla ΔR(X1) oraz o 12,1% dla A0(X2).
Pozostałe czynniki wykazują niekorzystny wpływ - wraz z ich wzrostem od dolnego do górnego poziomu, wielkość współczynnika Uws rośnie:
- o 2,2% dla bf(X3),
- o 25,8% dla Ug,
- o 8,2% dla Uf(X5).
Opisany charakter wpływu czynników odzwierciedla również wykres ( RYS. 4 ), na którym pokazano graficzną zależność Uws= ƒ(ΔR, Ao) dla: bf= 0,09 m, Ug= 0,70, Uf= 1,10 W/(m2·K).
![RYS. 4. Zależność współczynnika przenikania ciepła okna Uws, [W/(m2·K)], od dodatkowego oporu cieplnego osłony przeciwsłonecznej ΔR, [(m2·K)/W], oraz pola powierzchni okna Ao, m2, przy szerokości elementów ramy bf = 0,09 m oraz współczynnikach przenikania ciepła oszklenia Ug = 0,70 i ramy Uf = 1,10 W/(m2·K); rys. archiwum autorów RYS. 4. Zależność współczynnika przenikania ciepła okna Uws, [W/(m2·K)], od dodatkowego oporu cieplnego osłony przeciwsłonecznej ΔR, [(m2·K)/W], oraz pola powierzchni okna Ao, m2, przy szerokości elementów ramy bf = 0,09 m oraz współczynnikach przenikania ciepła oszklenia Ug = 0,70 i ramy Uf = 1,10 W/(m2·K); rys. archiwum autorów](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/b-wplyw-oslony-przeciwslonecznej-rys4.jpg)
RYS. 4. Zależność współczynnika przenikania ciepła okna Uws, [W/(m2·K)], od dodatkowego oporu cieplnego osłony przeciwsłonecznej ΔR, [(m2·K)/W], oraz pola powierzchni okna Ao, m2, przy szerokości elementów ramy bf = 0,09 m oraz współczynnikach przenikania ciepła oszklenia Ug = 0,70 i ramy Uf = 1,10 W/(m2·K); rys. archiwum autorów
Najbardziej dokładnie został poddany analizie wpływ szukanego czynnika ΔR(X1).
Zauważono, że w modelu (9) jest kilka efektów interakcji tego czynnika z innymi czynnikami (0,012X1X2, –0,002X1X3, –0,022X1X4, –0,006X1X5). Analizując te efekty, wykryto, że wpływ czynnika X1 wzmacnia się ze wzrostem czynników X3, X4, X5 oraz słabnie ze wzrostem X2.
Dla pełnego przeanalizowania X1 należało oszacować jego wpływ przy odpowiednich skrajnych wartościach X2, X3, X4, X5, które są ograniczone przyjętym w badaniu zakresem zmienności. Po podstawieniach wartości tych czynników do modelu (9) i wykonaniu obliczeń symulacyjnych wykryto dodatkową informację o wpływie czynnika ΔR(X1).
Okazało się, że:
- dla okna z polem powierzchni Ao= 3,60 m2; bf= 0,07 m; Ug= 0,5 i Uf= 0,9 W/(m2·K) zmiana czynnika ΔR(X1) z 0,08 do 0,36 (m2·K)/W powoduje obniżenie współczynnika Uwsod 0,716 do 0,598 W/(m2·K), tj. spadek o 16,5%;
- natomiast dla okna z polem powierzchni Ao= 1,20 m2; bf= 0,11 m; Ug= 0,9 i Uf= 1,3 W/(m2·K) zmiana czynnika ΔR(X1) w tym samym zakresie powoduje obniżenie współczynnika Uwsod 1,176 do 0,89 W/(m2·K), tj. spadek znacznie większy i wynoszący 24,3%.
Dodatkowo oszacowano wahania współczynnika Uws od czynnika ΔR(X1) w centrum Gp przestrzeni czynnikowej. Wykryto, że zmiana czynnika ΔR(X1) z 0,08 do 0,36 (m2·K)/W dla okna z polem powierzchni Ao= 2,40 m2, bf= 0,09 m, Ug= 0,7 i Uf= 1,1 W/(m2·K) powoduje obniżenie współczynnika Uws z 0,926 do 0,724 W/(m2·K), tj. spadek o 21,8%.
Uzyskane wyniki obliczeń w pełnym stopniu określają wpływ czynnika ΔR, charakteryzującego zastosowaną osłonę przeciwsłoneczną, na wielkość współczynnika Uws okna wykonanego z PVC.
Wnioski
1. Opracowany deterministyczny model matematyczny pozwolił oszacować charakter i stopień wpływu drewnianych osłon przeciwsłonecznych o różnej przepuszczalności na współczynnik przenikania ciepła okna Uws.
2. Wpływ czynnika ΔR na wartość Uws wzmacnia się ze wzrostem szerokości elementów ramy bf, współczynników przenikania ciepła oszklenia Ug i ramy Uf oraz słabnie ze wzrostem powierzchni okna Ao.
3. Zmiana dodatkowego oporu cieplnego osłony przeciwsłonecznej ΔR z 0,08 do 0,36 (m2·K)/W:
- dla okna Ao= 3,60 m2, bf= 0,07 m, Ug= 0,5 i Uf= 0,9 W/(m2·K) powoduje spadek współczynnika Uwso 16,5%,
- dla okna Ao= 1,20 m2, bf= 0,07 m, Ug= 0,5 i Uf= 0,9 W/(m2·K) spadek ten wynosi 24,3%.
Literatura
- S. Wall, "Zrównoważony rozwój w budownictwie - inicjatywy europejskie kształtujące nowe wymagania wobec wyrobów i obiektów budowlanych", "Materiały Budowlane" 3/2010, s. 43-45.
- J. Żurawski, "Energooszczędność w budownictwie cz. 20", "IZOLACJE" 11/12 2009.
- PN-EN ISO 10077-1:2007:2017-10, "Cieplne właściwości użytkowe okien, drzwi i żaluzji. Obliczanie współczynnika przenikania ciepła. Część 1: Postanowienia ogólne".
- PN-EN ISO 12631:2013-03:2017-10, "Cieplne właściwości użytkowe ścian osłonowych. Obliczanie współczynnika przenikania ciepła".
- M. Korzyński, "Metodyka eksperymentu. Planowanie, realizacja i statystyczne opracowanie wyników eksperymentów technologicznych", WNT, Warszawa 2006.
- J. Gutenbaum, "Modelowanie matematyczne systemów", Wyd. EXIT, Warszawa 2003.
- B. Durakovic, "Design of Experiments Application, Concepts, Examples: State of the Art", "Periodicals of Engineering and Natural Sciences" vol. 5/2017, no. 3: 421-439.
- W. Jezierski, J. Borowska, "Parametry cieplne wieloskrzydłowej stolarki okiennej w budynkach mieszkalnych", "IZOLACJE" 6/2017.
- PN-EN 12519:2007, "Okna i drzwi. Terminologia".