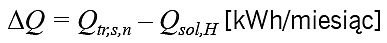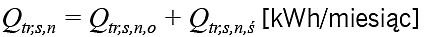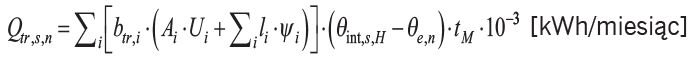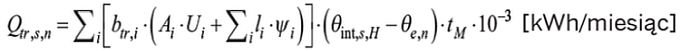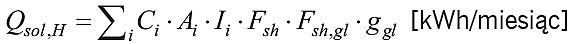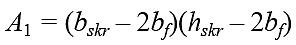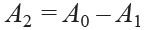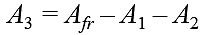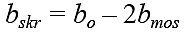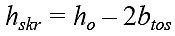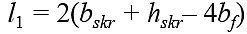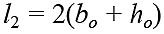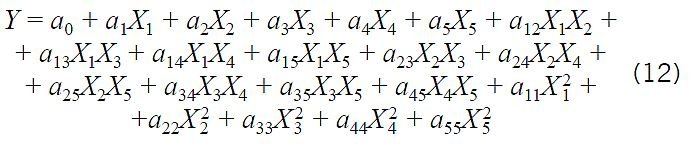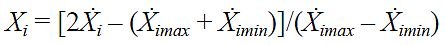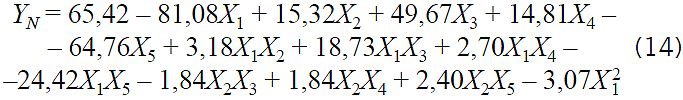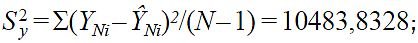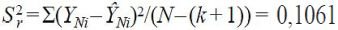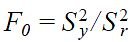Bilans cieplny fragmentu ściany osłonowej z oknem przy różnej orientacji
Heat balance of a curtain wall section with a window in different orientations

Ściana osłonowa każdego pomieszczenia w budynkach mieszkalnych najczęściej jest fragmentem składającym się z odcinka ściany pełnej i okna.
For. Milewski Sp. z o.o.
Obecne wymagania w zakresie ochrony termicznej budynków skłaniają naukowców i badaczy do poszukiwania takich rozwiązań architektoniczno‑budowlanych, by minimalizować straty, a maksymalizować zyski ciepła. W tym celu należy dobrać odpowiednie wymiary przegród zewnętrznych i otworów oraz materiały do ich wykonania tak, by osiągnąć możliwie najbardziej korzystne parametry izolacyjności. Aby tego dokonać, trzeba poddać optymalizacji niektóre parametry badanych elementów budynku, np. fragmentu ściany zewnętrznej z oknem, czego wynikiem będą wiarygodne obliczenia pokazujące, jak powinny być ukształtowane i wykonane przegrody.
Zobacz także
Fiberglass Fabrics sp. z o.o. Tynki i farby w dużych inwestycjach budowlanych

Przy projektowaniu i realizacji dużych inwestycji, takich jak osiedla mieszkaniowe, biurowce czy obiekty użyteczności publicznej, kluczowe znaczenie ma wybór odpowiednich materiałów wykończeniowych. Nie...
Przy projektowaniu i realizacji dużych inwestycji, takich jak osiedla mieszkaniowe, biurowce czy obiekty użyteczności publicznej, kluczowe znaczenie ma wybór odpowiednich materiałów wykończeniowych. Nie do przecenienia jest rola tynków i farb, które wpływają na wygląd budynków, a także na ich trwałość i komfort użytkowania.
Connector.pl Nowoczesne piany poliuretanowe – szczelne i trwałe ocieplenie budynku

Firma Connector.pl to największy polski dystrybutor materiałów do produkcji kompozytów, będący liderem na rynku od ponad 30 lat. W swojej ofercie posiadamy szeroką gamę produktów, a wśród nich znakomitej...
Firma Connector.pl to największy polski dystrybutor materiałów do produkcji kompozytów, będący liderem na rynku od ponad 30 lat. W swojej ofercie posiadamy szeroką gamę produktów, a wśród nich znakomitej jakości piany PUR otwarto- i zamkniętokomórkowe.
Czytaj całość »
M.B. Market Ltd. Sp. z o.o. Czy piana poliuretanowa jest palna?
W artykule chcielibyśmy przyjrzeć się bliżej temu aspektowi i rozwiać wszelkie wątpliwości na temat palności pian poliuretanowych.
W artykule chcielibyśmy przyjrzeć się bliżej temu aspektowi i rozwiać wszelkie wątpliwości na temat palności pian poliuretanowych.
Czytaj całość »
O czym przeczytasz w artykule? |
Abstrakt |
|---|---|
|
W artykule przedstawiono oryginalne badanie bilansu cieplnego fragmentu ściany osłonowej z jednoskrzydłowym oknem z PVC w budynku mieszkalnym w zależności od pola powierzchni okna, szerokości elementów ramy, współczynników przenikania ciepła oszklenia i ramy oraz przepuszczalności energii promieniowania słonecznego dla orientacji północnej w warunkach klimatycznych Białegostoku. Dane uzyskane przy realizacji eksperymentu obliczeniowego pozwoliły opracować deterministyczny model matematyczny opisujący tę zależność. Po analizie charakteru wpływu czynników wykonano symulacyjne obliczenia i uzyskano informacje o bilansie cieplnym dla ściany z oknem zorientowanymi do innych stron horyzontu. Informacja może być przydatna dla projektantów, naukowców, producentów i użytkowników stolarki okiennej. Heat balance of a curtain wall section with a window in different orientationsThe article presents an original research study on the thermal balance of a curtain wall section with a single-winged PVC window in a residential building depending on the window area, frame width, glazing and frame heat transfer coefficients, as well as solar energy transmittance for northern orientation in Bialystok’s climatic conditions. Based on the data obtained during the computational experiment, a deterministic mathematical model describing this relationship was developed. Following the analysis of the character of the coefficients’ influence, simulation calculations were made and information about the thermal balance for the wall with the window oriented to other sides of the horizon was obtained. Information can be useful for designers, scientists, producers and users of window joinery. |
Procedura optymalizacyjna dla bilansu cieplnego wycinka ściany zewnętrznej wraz z otworem okiennym polega na zsumowaniu zysków i strat ciepła przez analizowane przegrody. Najkorzystniejszy jest taki przypadek, gdy bilans cieplny jest ujemny – wówczas w okresie rocznym zyski przewyższą straty i wycinek przegrody będzie więcej energii dawał dla budynku niż z niego pozyskiwał. W przeciwnym wypadku, gdy wyniki bilansu będą dodatnie, straty ciepła będą przewyższały zyski.
Straty ciepła przez przenikanie w budynku mieszkalnym zależą przede wszystkim od współczynników przenikania ciepła i powierzchni elementów przegród budowlanych. Natomiast na sumę zysków słonecznych wpływają: natężenie promieniowania słonecznego dla strefy, w której znajduje się budynek, kąt nachylenia okien, zacienienie powierzchni oszklenia, orientacja okien według stron świata, a także przepuszczalność promieniowania słonecznego dla części szklonej okna [1].
Kilkoro badaczy już wcześniej podjęło się poszukiwania za pomocą metod matematycznych najlepszego, ze względu na wybrane kryterium, rozwiązania stolarki okiennej. Niektórzy z nich próbowali optymalizować parametry okien. Jednakże nieliczni analizowali zmienną orientację okien względem stron świata przy wyliczaniu bilansu cieplnego [2–3].
W publikacji [2] autor przeprowadził optymalizację parametrów energetycznych okien, gdzie kluczowy wpływ na wyniki obliczeń miały strefy klimatyczne, w których znajdował się analizowany budynek. Usytuowanie budynku w różnych lokalizacjach na mapie Polski i w różnej orientacji względem stron świata skutkuje innymi składowymi natężenia promieniowania słonecznego padającego na przegrody przeszklone, a w rezultacie powoduje inne zyski solarne. Artykuł opisuje model matematyczny noszący znamiona optymalizacji, a wyniki obliczeń są sumą zysków i strat energii przez okno.
Analizie zostały poddane współczynniki przenikania ciepła U dla poszczególnych części okna i współczynnik transmitancji g, jednakże nie uwzględniono innych kluczowych parametrów, jakie powinny być wzięte pod uwagę. Natomiast w pracy [3] autorzy wyliczyli energochłonność budynku mieszkalnego przy zmieniającym się udziale okien w stosunku do udziału przegród pełnych.
Została także podjęta próba optymalizacji powierzchni okien w zależności od usytuowania budynku względem stron świata. Jednakże parametry energetyczne stolarki okiennej nie ulegały zmianie, a co za tym idzie można uznać, że publikacja odnosi się do optymalizacji parametrów technicznych, a nie energetycznych okien.
Dodatkowo autorzy stwierdzili, że ze względu na wielorakość konstrukcji budowlanych powinno zostać opracowane indywidualne podejście do każdego obiektu, by dokładnie określić optymalną powierzchnię okien. Zdaniem autorów należy także rozwinąć analizę na sezon letni, wraz z uwzględnieniem konieczności poniesienia nakładów energetycznych na klimatyzację pomieszczeń, do których docierają nadmierne solarne zyski ciepła.
Celem danego badania jest więc analiza bilansu cieplnego fragmentu ściany osłonowej z jednoskrzydłowym oknem z PVC w budynku mieszkalnym w zależności od pola powierzchni okna, szerokości elementów ramy, współczynników przenikania ciepła oszklenia i ramy oraz przepuszczalności energii promieniowania słonecznego w warunkach klimatycznych Białegostoku dla orientacji północnej z opracowaniem modelu matematycznego na podstawie danych z eksperymentu obliczeniowego oraz uzyskanie za pomocą obliczeń symulacyjnych informacji o bilansie cieplnym tego fragmentu przy orientacji do innych stron horyzontu.
Metoda obliczania bilansu cieplnego fragmentu ściany osłonowej z oknem
Bilans cieplny fragmentu ściany osłonowej z oknem ΔQ rozpatrywano jako różnicę rocznych strat i zysków ciepła przez tę przegrodę oraz określono według wzorów podanych w pracy [4]:
![]() (1)
(1)
![]() (2)
(2)
Całkowita ilość ciepła przenoszonego ze strefy ogrzewanej przez przenikanie dla badanego fragmentu ściany z oknem może być obliczona według wzoru:
![]() (3)
(3)
Zyski ciepła od promieniowania słonecznego przez okno:
![]() (4)
(4)
gdzie:
Qtr,s,n – całkowita ilość ciepła przenoszonego ze strefy ogrzewanej przez przenikanie dla badanego fragmentu ściany z oknem, [kWh/miesiąc],
Qtr,s,n,ś – straty ciepła przez przenikanie przez ścianę, [kWh/miesiąc],
Qtr,s,n,o – straty ciepła przez przenikanie przez okno, [kWh/miesiąc],
Qsol – zyski ciepła słonecznego przez okno, [kWh/miesiąc],
θint.s.H – temperatura wewnętrzna dla okresu ogrzewania w budynku, przyjmowana zgodnie z wymaganiami zawartymi w przepisach techniczno-budowlanych, [°C],
θe,n – średnia temperatura powietrza zewnętrznego w analizowanym okresie miesięcznym według danych dla najbliższej stacji meteorologicznej, [°C],
btr,i – współczynnik redukcyjny obliczeniowej różnicy temperatur, [–],
Ai – pole powierzchni i-tego składnika fragmentu ściany z oknem (A 1 – oszklenia; A2 – ramy okiennej; A3 – ściany pełnej), [m2],
Ui – współczynnik przenikania ciepła i-tego składnika fragmentu ściany z oknem (U1 – oszklenia; U 2 – ramy okiennej; U 3 – ściany pełnej), [W/(m2∙K)],
ψi – liniowy współczynnik przenikania ciepła i-tego mostka termicznego, obejmuje współczynniki: ψ1 – mostka liniowego na styku szyba–rama; ψ2 – mostka liniowego na styku rama–ściana, [W/(m∙K)],
li – długość i-tego liniowego mostka termicznego, obejmuje: l1 – długość mostka liniowego na styku szyba–rama; l2 – długość mostka liniowego na styku rama–ściana, [m],
C – udział pola powierzchni płaszczyzny szklonej do całkowitego pola powierzchni okna, [–],
Ao – pole powierzchni okna w świetle otworu w przegrodzie, [m2],
Ij – wartość energii promieniowania słonecznego w j-tym miesiącu na płaszczyznę, w której usytuowane jest okno o powierzchni Ao wg danych dotyczących najbliższego punktu pomiarów promieniowania słonecznego, [kWh/(m2∙miesiąc)],
ggl – całkowita przepuszczalność energii promieniowania słonecznego dla przezroczystej części okna, [–],
Fsh – czynnik redukcyjny ze względu na zacienienie od przegród zewnętrznych, [–],
Fsh,gl – czynnik redukcyjny ze względu na zacienienie dla ruchomych urządzeń zacieniających, [–].
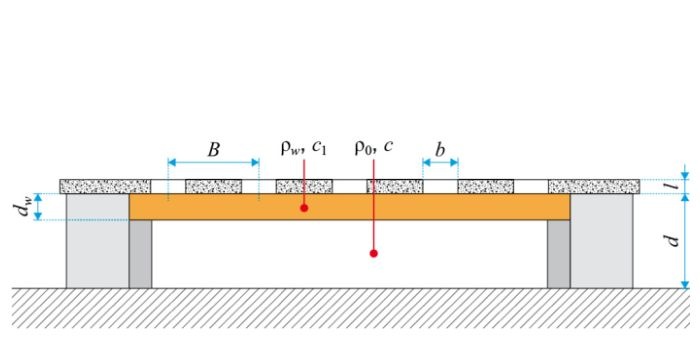
Ze wzorów, opracowanych przez autorów, obliczano wartości pól powierzchni A1, A2, A3:


RYS. 1. Schemat blokowy obliczania bilansu cieplnego ΔQ fragmentu ściany osłonowej z oknem; rys.: W. Jezierski, J. Borowska
gdzie:
ho, hskr – wysokość, odpowiednio: okna; pojedynczego skrzydła, [m],
bo, bskr, bƒ, bmos, btos – szerokość, odpowiednio: okna; pojedynczego skrzydła; elementów ramy skrzydłowej; stojaków i ramiaków ościeżnicy, [m] (w terminologii według [5]),
Aƒr – powierzchnia fragmentu ściany osłonowej z oknem, [m2],
A0 – powierzchnia okna, [m2],
A0 = A1 + A2.
Do realizacji eksperymentu obliczeniowego, związanego z określeniem bilansu cieplnego ΔQ, autorzy wybrali pięć zmiennych wejściowych i stworzyli algorytm, którego schemat blokowy pokazano na RYS. 1. Algorytm ten określał kolejność wykonywania operacji procesu obliczeniowego i posłużył jako podstawa do opracowania autorskiego programu do obliczeń.
Badane warianty ściany osłonowej z oknem
W badaniu przyjęto najprostsze rozwiązanie okna – okno jednoskrzydłowe. Rozmiary okna zmieniały się w szerokim zakresie w celu wykrycia efektów energii promieniowania słonecznego przenikającej przez oszklenie i tworzącej zyski ciepła.
Warunkowo przyjęto, że przy określaniu bilansu ciepła badane fragmenty przegrody zewnętrznej z oknem będą zorientowane po kolei według 8 stron horyzontu: N, NE, E, SE, S, SW, W, NW.
Odcinek ściany wybrany jako fragment ściany osłonowej przyjęto w rozmiarze 2,70×3,60 = 9,72 m2.
Z uwzględnieniem najprostszego rozwiązania okna zostały wybrane następujące warianty stolarki okiennej:
- powierzchnia
2,19 (1,48×1,48) m2;
3,28 (1,81×1,81) m2;
4,37 (2,09×2,09) m2; - proporcje (stosunek wysokości okna do jego szerokości) – 1:1;
- liczba skrzydeł – 1.
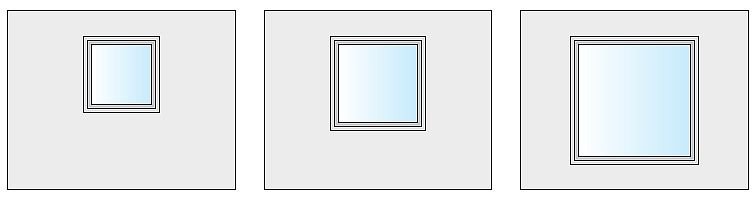
Schematy badanych wariantów podano na RYS. 2.
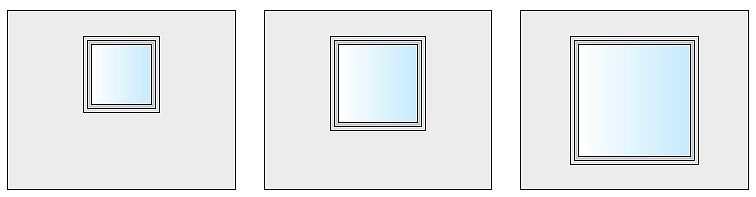
RYS. 2. Schematy badanych wariantów fragmentu ściany osłonowej z oknem; rys.: W. Jezierski, J. Borowska
Model matematyczny bilansu cieplnego fragmentu ściany osłonowej z oknem
Do osiągnięcia sformułowanego celu jako metodę badawczą zastosowano modelowanie matematyczne, które pozwala za pośrednictwem zależności matematycznych opisywać funkcjonowanie badanego obiektu, określać parametry wyjściowe, wykonywać poszukiwanie optymalnych wartości parametrów obiektu [6].
Stosowanie modelowania matematycznego pozwala zrezygnować z modelowania fizycznego, skrócić objętość próbkowania, obniżyć pracochłonność badania. Głównym komponentem w takim układzie jest model matematyczny.
Do najbardziej uniwersalnych zadań przy stosowaniu modeli matematycznych należą rozwiązanie zadań optymalizacyjnych oraz wyznaczenie niektórych zmiennych, podczas gdy innym zmiennym modelu narzucamy wartości przez nas zbadane lub zmierzone.
Proces wyznaczania zmiennych zależnych nazywa się rozwiązywaniem równań modelowych. Jedną z metod rozwiązywania równań modelowych jest symulacja, dla której charakterystyczne jest to, że zmiennymi niezależnymi modelu są zmienne odpowiadające wielkościom wejściowym systemu rzeczywistego [6].
Przy opracowaniu modelu matematycznego dąży się do jego praktycznej utylitarności oraz skuteczności. Takie cechy można osiągnąć, opracowując krótkie modele, w których wykorzystano najważniejsze czynniki interesujące odbiorców stolarki okiennej.
Jako funkcję celu YN wybrano roczny bilans cieplny fragmentu ściany osłonowej z oknem ΔQ [kWh/miesiąc]. Bilans cieplny ma wyraźny sens fizyczny, jest wielkością mierzalną i jednoznaczną.
Na podstawie wstępnej analizy wytypowano również najważniejsze z czynników, określające straty i zyski ciepła. Przeanalizowano również podstawowe wymagania stawiane czynnikom – powinny być one sterowalne, mierzalne, jednoznaczne, niesprzeczne i wzajemnie niezależne [6].
Po analizie do badania przyjęto następujące czynniki:
- pole powierzchni okna A 0 (czynnik X1);
- szerokość elementów ramy bƒ (czynnik X2);
- współczynnik przenikania ciepła oszklenia U1 (czynnik X3);
- współczynnik przenikania ciepła ramy U2 (czynnik X4);
- przepuszczalność energii promieniowania słonecznego przez szkło g (czynnik X5).
Te czynniki najwyraźniej określają wkład w wielkość bilansu cieplnego, który kształtuje się poprzez straty i zyski energii.
Szóstego czynnika, czyli orientacja okien według stron horyzontu α, mimo wspomnienia o tym w celu badania, nie udało się uwzględnić w modelu. Czynnik ten należało przyjąć na ośmiu poziomach, czyli zgodnie z liczbą stron horyzontu. Jednak wymaganie z zakresu teorii planowania eksperymentu odnośnie jednakowej liczby poziomów dla wszystkich czynników nie pozwoliło orientacji dołączyć do tworzonego modelu.
Przypuszczano, że szukaną zależność YN = ƒ(X1, X2, X3, X4, X5) może opisywać wielomian drugiego stopnia w postaci:

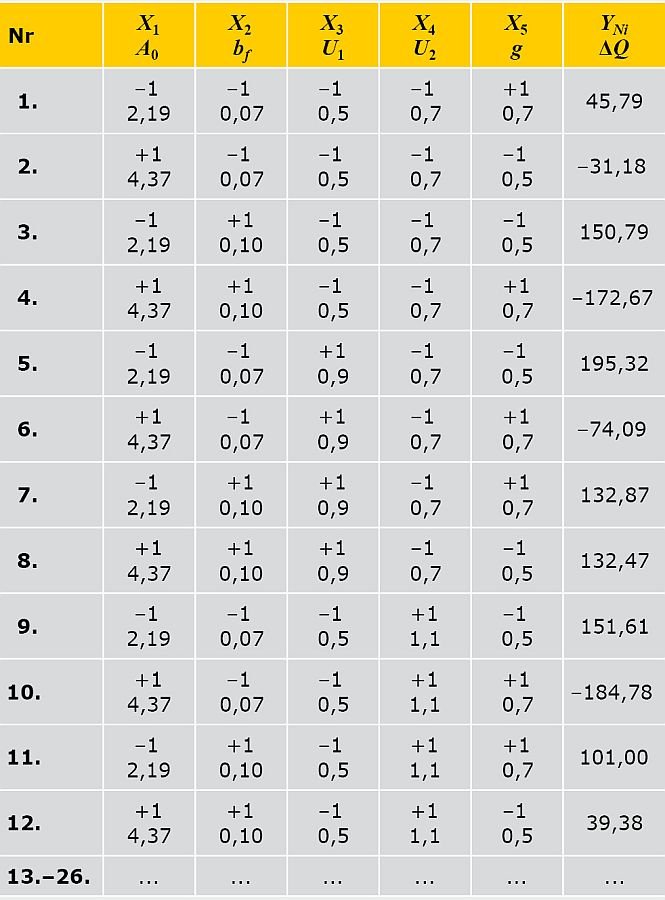
Do uzyskania danych dla opisu tej zależności przeprowadzono 5-czynnikowy eksperyment obliczeniowy według planu drugiego stopnia ( TABELA 1 ).
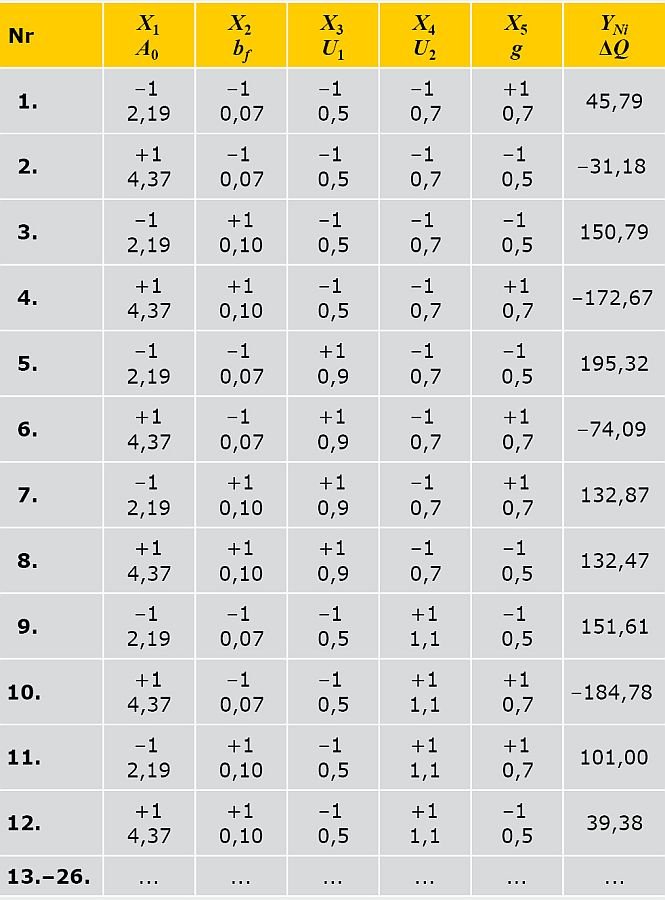
TABELA 1. Macierz planowania i wyniki eksperymentu obliczeniowego,
gdzie: X1, X2, X3, X4, X5 – kodowane czynniki;
A 0, bƒ, U1, U2, g – naturalne czynniki;
YNi – wyniki obliczeń bilansu cieplnego fragmentu ściany osłonowej z oknem ΔQ
Zastosowano kompozycyjny symetryczny trójpoziomowy plan, zawierający 26 prób [7].
Do wyliczenia wartości YNi w 26 wierszach planu wykorzystano oprogramowanie Microsoft Excel.
Przed rozpoczęciem obliczeń wykonano uzasadniony wybór zakresu zmienności czynników oraz wartości zmiennych stałych, od których zależą także efekty wpływu rozpatrywanych czynników.
Pole powierzchni okna A 0 (czynnik X1) na dolnym poziomie przyjęto równe 2,19 m2; na górnym – 4,37 m2; na średnim – 3,28 m2.
Szerokość elementów ramy skrzydłowej bƒ (czynnik X2) na dolnym poziomie przyjęto 0,070 m; na górnym – 0,100 m; na średnim – 0,085 m. Wybrany zakres obejmuje szerokości elementów ram dla okien z PCV.
Współczynnik przenikania ciepła oszklenia U1 (czynnik X3) przyjęto na poziomach 0,500; 0,700; 0,900 W/(m2∙K).
Współczynnik przenikania ciepła ramy U2 (czynnik X4) przyjęto na poziomach 0,700; 0,900; 1,100 W/(m2∙K). Takie zakresy zmienności tego czynnika charakteryzują obecnie stosowane profile z PVC.
Przepuszczalność energii promieniowania słonecznego przez szkło g (czynnik X5) przyjęta została na poziomach 0,5; 0,6; 0,7 zgodnie z danymi zawartymi w normie PN-EN ISO 13790-2008 [8].
Wyżej wymienione wartości naturalne czynników Ẋ1, Ẋ2, Ẋ3, Ẋ4, Ẋ5 i odpowiadające im wartości unormowane X1, X2, X3, X4, X5 przedstawiono w TABELI 1.
Według [7] przejście z wartości naturalnych Ẋi do unormowanych Xi wyraża się wzorem:
![]() (13)
(13)
gdzie:
Ẋi, Ẋimax, Ẋimin – odpowiednio bieżące, maksymalne i minimalne wartości naturalne i-tego czynnika.
Pozostałe zmienne wejściowe przyjęto na stałym poziomie.
- Szerokość stojaków i ramiaków ościeżnicy – 0,035 m.
- Pole powierzchni fragmentu ściany osłonowej przyjęto 9,72 m2.
- Współczynnik przenikania ciepła ściany pełnej przyjęto na aktualnym poziomie wymagań ochrony cieplnej U3 = 0,23 W/(m2∙K) [9].
- Liniowy współczynnik przenikania ciepła mostka na styku szyba–rama przyjęto ψ1 = 0,060 W/(m∙K), natomiast liniowy współczynnik przenikania ciepła mostka na styku rama–ściana ψ2 = 0,023 W/(m∙K) [10].
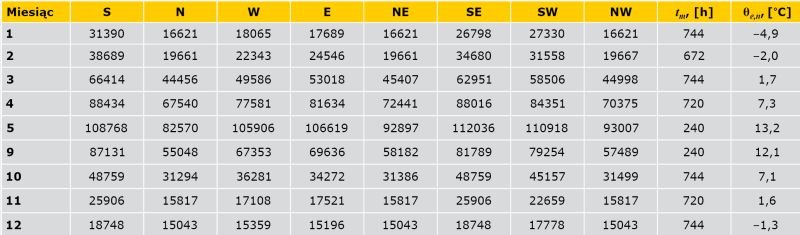
- Dane klimatyczne (θe,n, Ij) przyjęto dla Białegostoku według TABELI 2 [11].
- Orientację fragmentu ściany z oknem przy opracowaniu modelu wybrano jako północną.
![TABELA 2. Dane klimatyczne o promieniowaniu słonecznym I, [Wh/(m2∙miesiąc], średniomiesięcznej temperaturze powietrza zewnętrznego θe,n [°C], liczbie godzin grzewczych w miesiącu tm [h] dla miasta Białystok [11] TABELA 2. Dane klimatyczne o promieniowaniu słonecznym I, [Wh/(m2∙miesiąc], średniomiesięcznej temperaturze powietrza zewnętrznego θe,n [°C], liczbie godzin grzewczych w miesiącu tm [h] dla miasta Białystok [11]](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/b-bilans-cieplny-okien-tab2.jpg)
TABELA 2. Dane klimatyczne o promieniowaniu słonecznym I, [Wh/(m2∙miesiąc], średniomiesięcznej temperaturze powietrza zewnętrznego θe,n [°C], liczbie godzin grzewczych w miesiącu tm [h] dla miasta Białystok [11]
Na podstawie wyników obliczeń ( TABELA 1 ) przy zastosowaniu metody najmniejszych kwadratów [12] opracowano model matematyczny w postaci równania regresji zależności YN = ƒ(X1, X2, X3, X4, X5). Istotność współczynników równania oceniono za pomocą t-kryterium [7].
Metoda testowania współczynników została szczegółowo opisana przez autorów w publikacji [13].
W wyniku testu siedem współczynników okazało się nieistotnych. Po ich usunięciu przyjęto postać końcową równania z k + 1 = 14 współczynnikami:

Potwierdzona została również adekwatność uzyskanego modelu według metody opisanej w [7, 13]. Model posiadał:


- R2 = 1,0.
Dodatkowo jakość aproksymacji danych opracowanym równaniem (13) oceniono według kryterium F [7].
Przy poziomie istotności α = 0,05 i liczbie stopni swobody
ƒ1 = N – 1 = 26 – 1 = 25;
ƒ2 = N – (k + 1) = 26 – 21 = 5
okazało się, że wartość obliczeniowa kryterium ![]() = 98814,514 wielokrotnie przekracza wartość tabelaryczną F0,05;25;5 = 4,525 [7], co świadczy o wysokiej jakości uzyskanego modelu.
= 98814,514 wielokrotnie przekracza wartość tabelaryczną F0,05;25;5 = 4,525 [7], co świadczy o wysokiej jakości uzyskanego modelu.
Do interpretacji wyników badania autorzy jako materiał pomocniczy wykorzystali również opracowany wcześniej model matematyczny bilansu cieplnego podobnego fragmentu dla tych samych czynników i warunków klimatycznych, lecz dla orientacji południowej. Model ten został opublikowany przez autorów w [14] i ma postać:

Modele (14) i (15) odzwierciedlają bilans cieplny tego samego fragmentu dla dwóch charakterystycznych kierunków stron horyzontu N i S, dla których, jak widać z TABELI 2, obserwuje się ekstremalne wartości energii promieniowania słonecznego w każdym miesiącu – minimalne dla kierunku N i maksymalne dla kierunku S. Ten fakt autorzy wykorzystują w dalszych rozważaniach przy analizie wyników.
Analiza wyników badania
Za pomocą równania regresji (14) przeanalizowano stopień i charakter wpływu poszczególnych czynników na roczny bilans cieplny ściany osłonowej z oknem ΔQ(YN) przy orientacji północnej.
Analizując opracowany model, wykryto, że w centrum Gp przestrzeni wieloczynnikowej, które charakteryzuje się współrzędnymi
A 0 = 3,28 m2;
bƒ = 0,085 m;
U 1 = 0,700 [W/(m2∙K)];
U 2 = 0,900 W/(m2∙K);
g = 0,6 [–]
wielkość bilansu cieplnego ΔQ wynosi 65,42 kWh/miesiąc.
Dodatni bilans oznacza, że w tym punkcie w okresie rocznym dla badanego fragmentu straty ciepła Qtr,s,n = 450,94 kWh/miesiąc przewyższają zyski ciepła Qsol,H= 385,52 o około 17,0%.
Przy szacowaniu wpływu poszczególnych czynników okazało się, że korzystny wpływ na wielkość ΔQ wykazują pole powierzchni okna A0 (X1) oraz przepuszczalność energii promieniowania słonecznego przez szkło g (X5). Przy zmianie wartości A0 od 2,19 do 4,37 m2 (pozostałe czynniki charakteryzują się współrzędnymi dla punktu Gp) następuje korzystny spadek bilansu cieplnego ΔQ od 143,43 do –18,73 kWh/miesiąc, tj. o –113,1%. Wynika to ze wzrostu zysków ciepła o 121,0%, chociaż ma miejsce również wzrost strat ciepła o 33,9% po zwiększeniu rozmiarów okna.
Dla czynnika g przy zmianie wartości od 0,5 do 0,7 następuje również korzystny spadek bilansu cieplnego ΔQ od 130,18 do 0,66 kWh/miesiąc, tj. o –99,5%. Związane jest to ze wzrostem wyłącznie zysków ciepła o 40,0% po zwiększeniu przepuszczalności energii promieniowania słonecznego przez szkło. Straty ciepła w tym przypadku są stałe.
Pozostałe czynniki wykazują niekorzystny wpływ, tj. wraz z ich wzrostem od dolnego do górnego poziomu wielkość bilansu cieplnego ΔQ wzrasta, czyli zmienia się w odwrotnym kierunku: od 50,10 do 80,74 (o 61,2%) dla bƒ(X2); od 15,75 do 115,09 (o 630,7%) dla U1 (X3); od 50,61 do 80,23 kWh/miesiąc (o 58,5%) dla U2 (X4).
Porównując modele (14) i (15) wykryto, że zmiana orientacji fragmentu ściany z oknem z kierunku S do N powoduje przede wszystkim niekorzystny wzrost średniej wartości bilansu cieplnego dla rozpatrywanej przestrzeni wieloczynnikowej (wyraz wolny zmienia się z –125,01 do 65,42 kWh/miesiąc). Słabnie również stopień wpływu czynników A0 (X1), bƒ(X2), g (X5). Jednak charakter i stopień wpływu pozostałych czynników, jak również efektów interakcji, pozostaje prawie bez zmiany. Uwzględniając to oraz analizując znaki efektów interakcji, uznano, że dla każdej orientacji najlepszymi parametrami, zapewniającymi minimalny bilans cieplny badanego fragmentu z maksymalnym udziałem zysków od słońca, są:
A 0 = 4,37 m2;
b ƒ = 0,07 m;
U 1 = 0,5 oraz U 2 = 0,7 W/(m2∙K);
g = 0,7 [–].
Odwrotnie, najgorszymi parametrami, powodującymi maksymalny bilans cieplny z minimalnym udziałem zysków od słońca dla każdej orientacji, są:
A 0 = 2,19 m2;
b ƒ = 0,10 m;
U 1 = 0,9 oraz U 2 = 1,1 W/(m2∙K);
g = 0,5 [–]
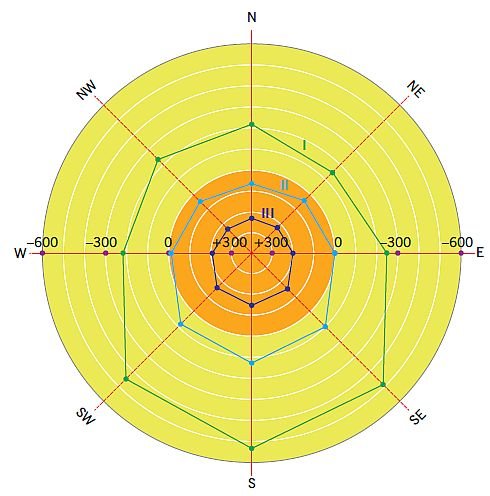
Dla tych dwóch zestawów parametrów, jak również dla parametrów w centrum przestrzeni wieloczynnikowej Gp (A0 = 3,28 m2; bƒ = 0,085 m; U1 = 0,7 i U2 = 0,9 W/(m2∙K); g = 0,6 [–]) za pomocą obliczeń symulacyjnych zostały obliczone wartości rocznego bilansu cieplnego ΔQ dla wszystkich ośmiu stron horyzontu w warunkach klimatu Białegostoku. Wyniki obliczeń pokazano w TABELI 3 oraz na RYS. 3 w postaci diagramu („róży”) bilansu cieplnego.
![TABELA 3. Wyniki obliczenia rocznego bilansu cieplnego fragmentu ściany osłonowej z oknem ΔQ, [kWh/miesiąc] dla różnych orientacji oraz zestawów parametrów okna TABELA 3. Wyniki obliczenia rocznego bilansu cieplnego fragmentu ściany osłonowej z oknem ΔQ, [kWh/miesiąc] dla różnych orientacji oraz zestawów parametrów okna](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/b-bilans-cieplny-okien-tab3.jpg)
TABELA 3. Wyniki obliczenia rocznego bilansu cieplnego fragmentu ściany osłonowej z oknem ΔQ, [kWh/miesiąc] dla różnych orientacji oraz zestawów parametrów okna
![RYS. 3. Zależność rocznego bilansu cieplnego fragmentu ściany osłonowej z oknem ΔQ, [kWh/miesiąc] od orientacji dla zestawów parametrów okna: I – A0 = 4,37 m2; bƒ = 0,07 m; U1 = 0,5 i U2 = 0,7 W/(m2∙K); g = 0,7 [–]; II – A0 = 3,28 m2; bƒ = 0,085 m; U1 = 0,7 i U2 = 0,9 W/(m2∙K); g = 0,6 [–]; III –A0 = 2,19 m2; bƒ = 0,10 m; U1 = 0,9 i U2 = 1,1 W/(m2∙K); g = 0,5 [–]; rys.: W. Jezierski, J. Borowska RYS. 3. Zależność rocznego bilansu cieplnego fragmentu ściany osłonowej z oknem ΔQ, [kWh/miesiąc] od orientacji dla zestawów parametrów okna: I – A0 = 4,37 m2; bƒ = 0,07 m; U1 = 0,5 i U2 = 0,7 W/(m2∙K); g = 0,7 [–]; II – A0 = 3,28 m2; bƒ = 0,085 m; U1 = 0,7 i U2 = 0,9 W/(m2∙K); g = 0,6 [–]; III –A0 = 2,19 m2; bƒ = 0,10 m; U1 = 0,9 i U2 = 1,1 W/(m2∙K); g = 0,5 [–]; rys.: W. Jezierski, J. Borowska](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/b-bilans-cieplny-okien-rys3.jpg)
RYS. 3. Zależność rocznego bilansu cieplnego fragmentu ściany osłonowej z oknem ΔQ, [kWh/miesiąc] od orientacji dla zestawów parametrów okna:
I – A0 = 4,37 m2; bƒ = 0,07 m; U1 = 0,5 i U2 = 0,7 W/(m2∙K); g = 0,7 [–];
II – A0 = 3,28 m2; bƒ = 0,085 m; U1 = 0,7 i U2 = 0,9 W/(m2∙K); g = 0,6 [–];
III –A0 = 2,19 m2; bƒ = 0,10 m; U1 = 0,9 i U2 = 1,1 W/(m2∙K); g = 0,5 [–];
rys.: W. Jezierski, J. Borowska
Z TABELI 3 widać, że zmiany poziomów czynników od najlepszych do najgorszych, jak i zmiany orientacji okien, okazują bardzo istotny wpływ na wartość rocznego bilansu cieplnego.
Opracowane przez autorów modele matematyczne (14) i (15) oraz diagram ( RYS. 3 ) pozwalają w sposób prosty wnosić korektę w ukształtowany na RYS. 3 wykres bilansu cieplnego, poprawiając w taki sposób zyski i straty ciepła poprzez odpowiedni dobór wartości badanych czynników.
Jak widać z RYS. 3, wykonywanie korekty przy orientacji okna w kierunku N lub S ma sens. Jeżeli mieszkańcom grozi przegrzanie pomieszczeń, to obniżając pole powierzchni okna A0 (X1) oraz przepuszczalność energii promieniowania słonecznego przez szkło g (X5) oraz/lub podwyższając szerokość elementów ramy bƒ(X2); współczynnik przenikania ciepła oszklenia U1 (X3); współczynnik przenikania ciepła ramy U2 (X4), projektant za pomocą modelu (15) może łatwo oszacować stopień poprawy bilansu cieplnego okna w kierunku S.
Jeżeli chcemy zwiększyć udział energii słonecznej przez okna w kierunku N, to należy podwyższyć pole powierzchni okna A0 (X1) oraz przepuszczalność energii promieniowania słonecznego przez szkło g (X5) oraz/lub obniżyć szerokość elementów ramy bƒ(X2); współczynnik przenikania ciepła oszklenia U1 (X3); współczynnik przenikania ciepła ramy U2 (X4).
Za pomocą modelu (14) wykonuje się kontrole stopnia poprawy bilansu cieplnego okna w kierunku N.
Uzyskane wyniki badania dają więc odpowiedź na pytanie na temat wpływu orientacji na bilans cieplny fragmentu ściany osłonowej z jednoskrzydłowym oknem z PVC o zmiennej powierzchni i właściwości termoizolacyjnych oraz tworzą operatywne narzędzie do korekty bilansu cieplnego okien różnej orientacji dla projektantów.
Wnioski
- Za pomocą oryginalnego badania opierającego się na wynikach eksperymentu obliczeniowego opracowano deterministyczny model matematyczny zależności bilansu cieplnego ΔQ fragmentu ściany osłonowej z oknem z PVC od wybranych czynników geometrycznych i fizykalnych przy orientacji północnej.
- Opracowane modele pozwoliły oszacować efekty wpływu badanych czynników i ustalić, że charakter ich wpływu w modelach przy orientacji północnej i południowej nie zmienia się. Pozwoliło to określić zestawy najlepszych i najgorszych parametrów okien ze względu na zapewnienie maksymalnego udziału zysków od słońca.
- Na podstawie obliczeń symulacyjnych uzyskano informację o bilansie cieplnym dla ściany z oknem zorientowanymi do wszystkich ośmiu stron horyzontu w warunkach klimatu Białegostoku. Wyniki obliczeń potwierdziły istotność wpływu wszystkich badanych czynników i pozwoliły stworzyć operatywne narzędzie do korekty bilansu cieplnego okien różnej orientacji dla projektantów.
Literatura
- Rozporządzenie Ministra Infrastruktury i Rozwoju z dnia 27 lutego 2015 r. w sprawie metodologii wyznaczania charakterystyki energetycznej budynku lub części budynku oraz świadectw charakterystyki energetycznej.
- W. Matusiak, „Optymalizacja energetyczna okien nowych i wymienianych. Część 3. Bilans energetyczny okien w sezonie grzewczym”, „Twój Filar” 1/2012, s. 15–18.
- B. Zając, M. Pomorski, „Określanie optymalnego udziału okien w budynku mieszkalnym”, „Zeszyty naukowe Politechniki Rzeszowskiej”, lipiec–wrzesień 2015, s. 269–276.
- Rozporządzenie Ministra Infrastruktury w sprawie metodologii obliczania charakterystyki energetycznej budynku i lokalu mieszkalnego lub części budynku stanowiącej samodzielną całość techniczno-użytkową oraz sposobu sporządzania wzorów świadectw i ich charakterystyki energetycznej.
- PN-EN 12519:2007, „Okna i drzwi. Terminologia”.
- J. Gutenbaum, „Modelowanie matematyczne systemów”, Wyd. EXIT, Warszawa 2003.
- M. Korzyński, „Metodyka eksperymentu. Planowanie, realizacja i statystyczne opracowanie wyników eksperymentów technologicznych”, WNT, Warszawa 2006.
- PN-EN ISO 13790-2008, „Energetyczne właściwości użytkowe budynków – Obliczanie zużycia energii do ogrzewania i chłodzenia”.
- Rozporządzenie Ministra Infrastruktury w sprawie warunków technicznych, jakim powinny odpowiadać budynki i ich usytuowanie z dnia 17 lipca 2015 r. (z późn. zmianami).
- PN-EN ISO 14683, „Mostki cieplne w budynkach. Liniowy współczynnik przenikania ciepła. Metody uproszczone i wartości orientacyjne”.
- Typowe lata meteorologiczne i statystyczne dane klimatyczne dla obszaru Polski do obliczeń energetycznych budynków (strona www. Ministerstwa Infrastruktury i Budownictwa): http://mib.gov.pl/2-Wskazniki_emisji_wartosci_opalowe_paliwa.htm#
- B. Durakovic, „Design of Experiments Application, Concepts, Examples: State of the Art”, „Periodicals of Engineering and Natural Sciences”, vol. 5/2017, no. 3, s. 421–439.
- W. Jezierski, J. Borowska, „Parametry cieplne wieloskrzydłowej stolarki okiennej w budynkach mieszkalnych”, „Izolacje” 6/2017.
- W. Jezierski, J. Borowska, „Analiza bilansu cieplnego fragmentu ściany osłonowej z oknem w budynku mieszkalnym”, „Izolacje” 11/12/2018.
- PN-EN 410:2001 „Szkło w budownictwie – Określenie świetlnych i słonecznych właściwości oszklenia”.