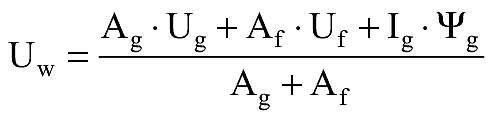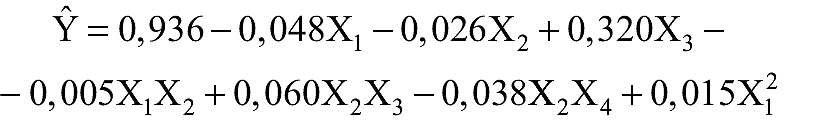Analiza parametrów cieplnych współczesnej stolarki okiennej
Analysis of thermal performance of modern window joinery

Nowoczesna stolarka okienna wyróżnia się wyższym poziomem izolacyjności termicznej i akustycznej, a także wysoką szczelnością i trwałością
Schüco
W dzisiejszych czasach w nowo wznoszonych budynkach stosuje się stolarkę okienną nowej generacji, wyróżniającą się wyższym poziomem izolacyjności termicznej i akustycznej, wysoką szczelnością i trwałością, a także dobrą estetyką. Konsumenci decydują się na okna w dużych rozmiarach, nawet kosztem zmniejszenia powierzchni ścian zewnętrznych.
Zobacz także
BREVIS S.C. Czy nawiewniki w oknach są obowiązkowe – najważniejsze Informacje

Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu...
Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu uniknięcia negatywnych skutków zbyt dużej wilgotności, to już dyskomfort siedzenia w dusznym i nieprzewietrzonym pomieszczeniu zna każdy. Oprócz wentylacji grawitacyjnej do niedawna odpowiednią cyrkulację powietrza zapewniały nieszczelności w oknach. Jednak rozwój technologiczny i zwiększenie szczelności...
DAKO Jak wybrać drzwi do nowoczesnego domu?

Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie...
Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie aspekty trzeba zwrócić szczególną uwagę, wybierając drzwi zewnętrzne!
Czytaj całość »
RoletyAlu Sp. z o.o. Jak łatwo kupić rolety zewnętrzne przez internet?
Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość...
Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość złożenia zamówienia bezpośrednio u producenta rolet zewnętrznych pozwala wyeliminować pośredników, co skraca czas potrzeby na realizację zamówień i przekłada się na dużo niższe ceny.
Czytaj całość »Według Rozporządzenia Ministra Infrastruktury z dn. 12 kwietnia 2002 r. w sprawie warunków technicznych, jakim powinny odpowiadać budynki i ich usytuowanie [1],
- od stycznia 2014 r. współczynnik przenikania ciepła Uw okien wynosił maksymalnie 1,3 W/(m2·K),
- od stycznia 2017 r. jest to zaledwie 1,1 W/(m2·K).
Podczas doboru rodzaju stolarki należy porównywać jej parametry cieplne z tymi wartościami.
Niestety dla współczesnej stolarki, która składa się z kilku elementów (oszklenia, ramy, słupków okiennych i rygli), często problematyczne jest uzyskanie informacji na temat współczynnika przenikania ciepła poszczególnych elementów. Nawet jeśli ma się takie informacje, konsumenci nie są w stanie obiektywnie ocenić właściwości cieplnych okien czy określić ich współczynnik przenikania ciepła w całości.
Nie zawsze można wyczytać też wszystkie informacje z reklam i ulotek marketingowych oferowanych przez producentów. Zazwyczaj są w nich podane 1-2 parametry cieplne i informacja odnośnie dźwiękoszczelności. Reszta danych to często chwyty marketingowe.
Dzięki wykorzystaniu nowoczesnych technologii we współczesnej stolarce okiennej nie mamy już do czynienia z czynnikiem zakłócającym, który skłaniał właścicieli budynków do wymiany okien na doskonalsze - infiltracją powietrza.
W nowoczesnych oknach stosowane są zestawy uszczelek, które praktycznie uniemożliwiają swobodny przepływ powietrza przez okna, przez co wartość współczynnika przenikania ciepła całego okna (Uw) pozostaje niezmienna w trakcie jego eksploatacji. Tak więc, przy prawie wyeliminowanej filtracji powietrza, dla współczesnej stolarki okiennej można w dokładny sposób wyliczyć i przeanalizować parametry cieplne okien, jeśli zna się rozmiary i charakterystyki cieplne poszczególnych elementów.
Celem niniejszego artykułu jest analiza współczynnika przenikania ciepła współczesnej stolarki okiennej wykonanej z PVC, w zależności:
- od powierzchni okna,
- udziału powierzchni szklonej do powierzchni okna,
- współczynnika przenikania ciepła oszklenia
- oraz współczynnika przenikania ciepła ramy,
z oceną stopnia i charakteru wpływu tych czynników oraz określeniem ich wartości optymalnych na podstawie opracowanego deterministycznego modelu matematycznego. Do analizy na potrzeby tej publikacji wybrano okna dwóch popularnych firm.
Metoda obliczania współczynnika przenikania ciepła stolarki okiennej
Do obliczania współczynnika przenikania ciepła stolarki okiennej najbardziej przydatna i oczywista jest składnikowa metoda oceny, opisana w normie PN-EN ISO 12631:2013-03 [2].
Metoda ta dzieli fragment przegrody na pola powierzchni o różnych właściwościach cieplnych, a całkowity współczynnik przenikania ciepła oblicza się za pomocą ważonych powierzchniowo wartości U elementów składowych z dodatkowymi członami korekcyjnymi, uwzględniającymi wzajemne oddziaływania cieplne między tymi elementami.
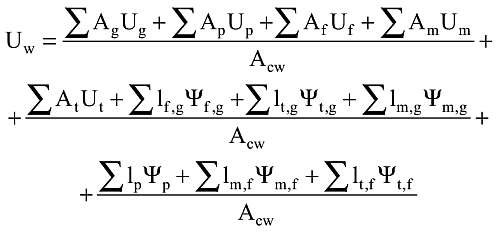
Według tej metody wartość współczynnika przenikania ciepła pojedynczego okna Uw należy obliczać zgodnie z równaniem:
 (1)
(1)
gdzie:
Ug, Up - współczynniki przenikania ciepła oszklenia i paneli,
Uf, Um, Ut - współczynniki przenikania ciepła ram, słupków okiennych i rygli,
ψf,g, ψt,g, ψm,g, ψp - liniowe współczynniki przenikania ciepła spowodowane połączonymi efektami cieplnymi elementu szklącego i ramy lub rygla, słupka albo samego panelu,
ψm,f, ψt,f - liniowe współczynniki przenikania ciepła spowodowane połączonymi efektami cieplnymi rama - słupek okienny lub rama - rygiel,
Acw - pole powierzchni ściany osłonowej,
Ag - całkowite pole powierzchni oszklenia,
Ap - całkowite pole powierzchni paneli,
Af - całkowite pole powierzchni ram.
W przypadku pojedynczego okna bez słupków okiennych i rygli można stosować wzór w postaci uproszczonej [3]:
 (2)
(2)
gdzie:
Uw - średni współczynnik przenikania ciepła okna [W/(m2·K)],
Uf - współczynnik przenikania ciepła ramy [W/(m2·K)],
Ug - średni współczynnik przenikania ciepła szyby [W/(m2·K)],
ψg,f - liniowy współczynnik przenikania ciepła mostka cieplnego na styku szyby z ramą okna [W/(m·K)],
Af - pole powierzchni ramy o współczynniku Uf [m2],
Ag - pole powierzchni szyby [m2],
lg - długość liniowego mostka cieplnego na styku szyby z ramą [m],
A0 - powierzchnia całkowita okna [m2].
Jak widać z ostatniego wzoru, nawet w najprostszym przypadku na współczynnik Uw wpływa sześć parametrów.
Zainteresowanie konsumentów może wzbudzać również siódmy parametr - powierzchnia całkowita okna, która związana jest z powierzchnią ramy i powierzchnią oszklenia warunkiem:
A0 = Ag + Af (3)
Na podstawie podanych wzorów autorzy stworzyli algorytm do wyliczania szukanego współczynnika przenikania ciepła okna Uw przy zmianie wartości wybranych czynników, który stanowił podstawę do opracowania modelu matematycznego.
Model matematyczny do określenia współczynnika przenikania ciepła okna
Do najbardziej uniwersalnych zadań przy stosowaniu modeli matematycznych należą rozwiązanie zadań optymalizacyjnych oraz wyznaczenie niektórych zmiennych, podczas gdy innym zmiennym modelom narzucamy wartości przez nas zbadane lub zmierzone. Proces wyznaczania zmiennych zależnych nazywa się rozwiązaniem równań modelowych. Jedną z metod rozwiązania równań modelowych jest symulacja, dla której charakterystyczne jest, że zmiennymi niezależnymi modelu są zmienne odpowiadające wielkościom wejściowym systemu rzeczywistego [4].
Zgodnie z przyjętym celem badania w niniejszej pracy jako funkcję celu przyjęto współczynnik przenikania ciepła stolarki okiennej Uw [W/(m2·K)] (odpowiedź Y). Chociaż współczynnik ten charakteryzuje przepuszczalność ciepła przez okna, jest on odwrotnością oporu cieplnego, to przyjęto go jako wielkość, która opisuje właściwości termoizolacyjne okna.
Przy opracowaniu modelu matematycznego dąży się do jego praktycznej utylitarności oraz skuteczności. Takie cechy można osiągnąć dzięki opracowaniu krótkich modeli, w których wykorzystano najważniejsze czynniki interesujące odbiorców stolarki okiennej.
Logicznie jest oczekiwać, że konsumentów stolarki okiennej mogą interesować właściwości termoizolacyjne okna w zależności od:
- powierzchni całkowitej okna A0 (czynnik X1),
- udziału pola powierzchni płaszczyzny szklonej do całkowitego pola powierzchni okna C (czynnik X2),
- współczynnika przenikania ciepła szyby Ug (czynnik X3)
- oraz współczynnika przenikania ciepła ramy Uf (czynnik X4).
Te czynniki można scharakteryzować jako odpowiadające podstawowym wymaganiom modelowania matematycznego – są sterowalne, mierzalne, wzajemnie niezależne oraz niesprzeczne [4]. Jednak dwa z nich nie są jednoznaczne:
- A0, ponieważ powierzchnia okna zależy od jego szerokości i wysokości, oraz
- C, który zależy od pól powierzchni szkła i ramy.
Jednoznaczność czynnikowi A0 można nadać, przyjmując wysokość okna jako wartość stałą, która w referencyjnych oknach w budynkach mieszkalnych wynosi 1,48 m. Jednoznaczność czynnikowi C zapewnia równość (3). Wymienione zmienne zostały przyjęte do analizy.

RYS. 1. Schemat blokowy wyliczania współczynnika przenikania ciepła okien w budynkach mieszkalnych; rys. archiwa autorów (W. Jezierski, J. Borowska)
Na RYS. 1 przedstawiono schemat blokowy wyliczania współczynnika przenikania ciepła okien w budynkach mieszkalnych. Zaproponowany algorytm obliczeń został zastosowany do realizacji eksperymentu obliczeniowego, którego wyniki stanowiły podstawę do opracowania deterministycznego modelu matematycznego współczynnika przenikania ciepła stolarki okiennej.
Przypuszczano, że szukaną zależność Y = f (X1, X2, X3, X4) może opisywać wielomian drugiego stopnia.
Do uzyskania danych dla opisu tej zależności przeprowadzono 4-czynnikowy eksperyment obliczeniowy według planu drugiego stopnia ( TABELA ). Przy czym zastosowano kompozycyjny trójpoziomowy symetryczny plan D-optymalny, mający wysoką efektywność statystyczną i zawierający 24 próby [5].
Do wyliczenia wartości Yi w 24 wierszach planu wykorzystano oprogramowanie Microsoft Excel. Ważną procedurę przed rozpoczęciem obliczeń jest wybór zakresu zmienności czynników oraz wartości zmiennych stałych, od których zależą efekty wpływu rozpatrywanych czynników.
Przy wyborze wartości autorzy opierali się na informacjach o stolarce okiennej różnych firm. Zgodnie ze zgromadzonymi danymi wykonano wybór poziomów wybranych czynników. Jako typowy wyrób pierwszej badanej firmy wskazano system z ramą wykonaną z PVC. Okno to miało system profili zaopatrzony w 7 komór, przy czym głębokość zabudowy to 82 mm.
Wartość współczynnika przenikania ciepła Uf ramy wynosi 0,9 W/(m2·K), a współczynnik przenikania ciepła kompleksowego wyrobu Uw to zaledwie - w zależności od rodzaju wzmocnienia - 0,79 W/(m2·K), gdy wzmocnienie jest ze stali, lub 0,6 W/(m2·K), jeśli wykorzystano wzmocnienie z włókna szklanego. Okno wyposażone było w układ trzech uszczelek - od zewnątrz, wewnątrz, a także w spienioną uszczelkę centralną, by mogło być jeszcze bardziej wodoszczelne i mniej przepuszczało powietrze.
Z kolei drugi badany system, również z ramą z PVC, charakteryzuje się wielokomorową geometrią - aż 7 komór w profilu ramy oraz 6 komór w profilu skrzydła.
Ważne, że sam system profili ma wartość współczynnika przenikania ciepła ramy Uf na poziomie 1,0 W/(m2·K).
Dzięki zastosowaniu szyby, dla której współczynnik przenikania ciepła Ug wynosi 0,7 W/(m2·K), a liniowy współczynnik przenikania ciepła ψg kształtuje się na poziomie 0,050 W/(m·K), całkowity współczynnik przenikania ciepła Uw gotowego wyrobu to zaledwie 0,91 W/(m2·K). Przy wykorzystaniu innego pakietu szybowego, właściwości termoizolacyjności mogą być jeszcze lepsze.
Należy zaznaczyć, że jeśli współczynnik Uw jest niższy niż 0,9 W/(m2·K), wówczas wielkość okien i ich liczba jest dowolna. Gdy ma on wyższą wartość, niestety należy dostosować się do obowiązujących wymagań i spełnić warunki dotyczące powierzchni przegród przezroczystych w pomieszczeniach [1].
Przy wyborze zakresu zmienności czynników, pole powierzchni okna A0 (X1) na średnim poziomie przyjęto równe 1,84 m2, tj. odpowiednie polu powierzchni okna referencyjnego [6], którego wymiary wynoszą kolejno: 1,48 m - wysokość i 1,23 m - szerokość.
Dla zmienności tego czynnika przyjęto powierzchnie okna o 30% większą (2,367 m2) oraz o 30% mniejszą (1,274 m2) niż okno standardowe. Taki zakres zmienności powierzchni otworu okiennego pozwalał spełnić wymagania normowe odnośnie wielkości powierzchni przeszklonych w pomieszczeniach przeznaczonych na pobyt stały ludzi w budynkach mieszkalnych [1].
Udział pola powierzchni płaszczyzny szklonej do całkowitego pola powierzchni okna C ( X2 ) przyjęto na poziomie średnim równy 0,8 - gdy rama to już tylko 20% powierzchni całego okna, co jest charakterystyczne dla okien ze standardowym udziałem ramy.
- Dolny i górny poziomy tego czynnika przyjęto jako odpowiednio 0,65 - gdy rama stanowi 35% całkowitej powierzchni okna, oraz 0,95 – gdy rama stanowi zaledwie 5% całkowitej powierzchni okna. Taki zakres zmienności odpowiada wahaniom czynnika przy zmianie powierzchni całkowitej okna czy przy zastosowaniu udoskonalonych rozwiązań okien.
- Jako wartość średnią czynnika Ug (X3) przyjęto 0,6 W/(m2·K). Na górnym poziomie wybrano wartość równą 1,0 W/(m2·K). Taka wartość jest charakterystyczna dla okien starszych budynków i takich, które występują obecnie w większości domów jednorodzinnych.
- Najniższa wartość przyjęta została na poziomie 0,2 W/(m2·K). Producenci dążą, by produkować takie okna, które charakteryzować się będą tym parametrem na tak niskim poziomie, nie można było zatem pominąć tego faktu.
Wartość współczynnika przenikania ciepła ramy Uf (X4) na średnim poziomie przyjęto 0,95 W/(m2·K) i jest ona już osiągalna dla niektórych profili okiennych.
- Na poziomie najwyższym wybrano wartość równą 1,20 W/(m2·K). Jest to wartość typowa dla profilu wykonanego z drewna.
- Najniższą wartość współczynnika Uf przyjęto na poziomie 0,7 W/(m2·K). Takiej wysokości tego parametru jeszcze nie osiągnięto, ale ciągle trwają badania umożliwiające dokonanie tego.
Wymienione wartości naturalne czynników X1, X2, X3, X4 i odpowiadające im wartości kodowane przedstawiono w TABELI .
Pozostałe zmienne Ag, Af, lg we wzorach (2), (3) można wyliczyć na podstawie wartości wybranych czynników A0 i C. Wartość zmiennej ψg przyjęto jako stała i równa 0,10 W/(m·K) [7].
Na podstawie wyników obliczeń ( TABELA ) opracowano równanie regresji zależności Y = f(X1, X2, X3, X4).
Za pomocą t-kryterium oceniono istotność współczynników tego równania.
Uwzględniono, że w eksperymencie obliczeniowym w każdym punkcie planu mamy jeden wynik. Z tego powodu wykorzystano podejście opisane w " Statistische Versuchsplanung und -auswertung in der Stoffwirtschaft " [8], według którego dla każdego współczynnika obliczono tj = |bj|/Sbj, gdzie:
- bj - wartości współczynników równania regresji;
- Sbj - odchylenie standardowe j-tego współczynnika.
Do określenia Sbj obliczono wariancję S2 na podstawie sumy kwadratów odchyleń Σ (Yi – Ŷi)2. Wartości tj porównywano z wartością krytyczną t0,025;9 = 2,26 [8]. Przy tj < t0,025;9 współczynnik uznawany był jako nieistotny.
W wyniku testu sześć współczynników okazało się nieistotnych. Po ich usunięciu przyjęto postać końcową równania z k+1=9 współczynnikami:
 (4)
(4)
O adekwatności modelu uzyskanego z eksperymentu obliczeniowego zgodnie z zaleceniami " Statistische Versuchsplanung und -auswertung in der Stoffwirtschaft " [8] można sądzić, analizując: sumę kwadratów odchyleń Σ(Yi – Ŷi)2 ; wariancję błędów aproksymacji S2a ; współczynnik determinacji R2.
Dany model miał:
- Σ(Yi – Ŷi)2 = 0,0001;
- S2a= Σ(Yi – Ŷi)2/[N – (k+1)] = 0,0000066;
- R2 = 1,0000.
Jakość aproksymacji danych opracowanym równaniem oceniono również według kryterium F [8].
Przy poziomie istotności α = 0,05 i liczbie stopni swobody
- f1 = N – 1 = 24 – 1 = 23;
- f2 = N – (k + 1) = 24 – 9 = 15
okazało się, że wartość obliczeniowa kryterium F0 = S2y/S2a = 24887,5220 wielokrotnie przekracza wartość tabelaryczną F0,05;23;15 = 2,30 [9]. Potwierdza to adekwatność i skuteczność opracowanego równania regresji, a także jego przydatność do dalszej analizy.
Analiza wpływu wybranych parametrów na współczynnik przenikania ciepła okna
Interpretacja wpływu wybranych czynników na współczynnik przenikania ciepła okna wykonana została na podstawie analizy równania regresji (1). Dla lepszego zrozumienia wyników analizę przeprowadzono dla zmiennych w postaci naturalnej.
Przed analizą przypominamy, że interesują nas przede wszystkim okna o najniższym współczynniku przenikania ciepła Uw. Dzieli to umownie badane czynniki na korzystne czy pożądane, jeżeli wraz z ich wzrostem współczynnik Uw maleje, oraz niekorzystne, jeżeli wraz z ich wzrostem współczynnik Uw rośnie.
Najmocniejszy niekorzystny wpływ na współczynnik Uw wykazuje współczynnik przenikania ciepła oszklenia Ug.
Wykryto, że przy zmianie Ug od 0,2 W/(m2·K) do 1,0 W/(m2·K), współczynnik Uw zwiększa się równomiernie od 0,616 W/(m2·K) do 1,256 W/(m2·K), tj. wzrasta na 103,9%.
Zauważono również, że wpływ Ug wzmacnia się przy wzroście czynnika C i nie zależy od pozostałych czynników.
Na drugim miejscu według efektu oddziaływania lokuje się współczynnik przenikania ciepła ramy okiennej U f .
Wykryto, że współczynnik Uw zwiększa się równomiernie od 0,886 W/(m2·K) do 986 W/(m2·K) (na 11,3%) przy zmianie Uf od 0,7 W/(m2·K) do 1,2 W/(m2·K). Wpływ Uf słabnie przy wzroście czynnika C i nie zależy od pozostałych czynników.
Na trzecim miejscu plasuje się czynnik korzystny - powierzchnia okna A0.
Wykryto, że przy zmianie A0 od 1,274 m2 do 2,367 m2 współczynnik Uw zmniejsza się nierównomiernie od 0,999 W/(m2·K) do 0,903 W/(m2·K) (spadek o –9,6%). Zauważono, że dla czynników A0 i C ma miejsce synergizm ich wpływu, tj. każdy z nich przy ich wspólnym wzroście wpływa silniej, niż gdy wzrastają one osobno.
Na ostatnim miejscu znajduje się udział pola powierzchni płaszczyzny szklonej do całkowitego pola powierzchni okna C.
Wykryto, że współczynnik Uw zmniejsza się równomiernie od 0,962 W/(m2·K) do 910 W/(m2·K) (spadek o –5,4%) przy zmianie C od 0,65 do 0,95 Wpływ czynnika C wzmacnia się ze wzrostem czynników A0 i Uf oraz słabnie ze wzrostem b.
Opisany charakter wpływu czynników odzwierciedlają również wykresy na RYS. 2 i RYS. 3, na których pokazano graficzne zależności Uw= f (A0, C) oraz Uw= f (Ug, Uf), wykonane w systemie współrzędnych 3D.
![RYS. 2. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od współczynników przenikania ciepła szyby Ug [W/(m2·K)] i ramy okiennej Uf [W/(m2·K)] przy powierzchni okna A0=1820 m2 i udziale pola powierzchni płaszczyzny szklonej do całkowitego pola powierzchni okna C = 0,8; rys. archiwa autorów (W. Jezierski, J. Borowska) RYS. 2. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od współczynników przenikania ciepła szyby Ug [W/(m2·K)] i ramy okiennej Uf [W/(m2·K)] przy powierzchni okna A0=1820 m2 i udziale pola powierzchni płaszczyzny szklonej do całkowitego pola powierzchni okna C = 0,8; rys. archiwa autorów (W. Jezierski, J. Borowska)](https://www.izolacje.com.pl/media/cache/typical_view/data/202011/b-analiza-parametrow-stolarki-okiennej-rys2.jpg)
RYS. 2. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od współczynników przenikania ciepła szyby Ug [W/(m2·K)] i ramy okiennej Uf [W/(m2·K)] przy powierzchni okna A0=1820 m2 i udziale pola powierzchni płaszczyzny szklonej do całkowitego pola powierzchni okna C = 0,8; rys. archiwa autorów (W. Jezierski, J. Borowska)
![RYS. 3. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od powierzchni okna A0 [m2] i udziału pola powierzchni płaszczyzny szklonej do całkowitego pola powierzchni okna C przy współczynniku przenikania ciepła szyby Ug = 0,6 W/(m2·K) i ramy okiennej Uf = 0,95 W/(m2·K); rys. archiwa autorów (W. Jezierski, J. Borowska) RYS. 3. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od powierzchni okna A0 [m2] i udziału pola powierzchni płaszczyzny szklonej do całkowitego pola powierzchni okna C przy współczynniku przenikania ciepła szyby Ug = 0,6 W/(m2·K) i ramy okiennej Uf = 0,95 W/(m2·K); rys. archiwa autorów (W. Jezierski, J. Borowska)](https://www.izolacje.com.pl/media/cache/typical_view/data/202011/b-analiza-parametrow-stolarki-okiennej-rys3.jpg)
RYS. 3. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od powierzchni okna A0 [m2] i udziału pola powierzchni płaszczyzny szklonej do całkowitego pola powierzchni okna C przy współczynniku przenikania ciepła szyby Ug = 0,6 W/(m2·K) i ramy okiennej Uf = 0,95 W/(m2·K); rys. archiwa autorów (W. Jezierski, J. Borowska)
Nieoczekiwany charakter wpływu czynników A0 i C na współczynnik Uw można wyjaśnić faktem, że ze wzrostem A0 i C, mimo wzrostu wkładu w podwyższenie Uw szyby i ramy, maleje udział mostku termicznego na styku szkło-rama (najmocniejszego składnika Uw ) z powodu wolniejszego przyrostu jego długości w odniesieniu do powierzchni szkła i ramy.
W wyniku suma wkładów czy efektów tych trzech składników doprowadza do tego, że czynniki A0 i C w niewielkim stopniu obniżają współczynnik Uw. Jednak jest formalne wyjaśnienie, wynikające z niedokładności wzoru.
Na efekt sumaryczny wpływa również przyjęty zakres zmienności czynników. Dlatego autorzy nie przeceniają tego efektu sumarycznego.
Podczas wykonywania procedury optymalizacji wykryto, że uzyskana funkcja osiąga minimalną (najlepszą) wartość Uw,min = 0,480 W/(m2·K) przy następujących wartościach czynników:
- A0= 2,367 m2;
- C = 0,95;
- Ug= 0,20 W/(m2·K);
- Uf= 0,70 W/(m2·K).
Natomiast maksymalną (najgorszą) wartość Uw,max = 1,370 W/(m2·K) obserwuje się przy:
- A0= 1,274 m2;
- C = 0,65;
- Ug= 1,00 W/(m2·K);
- Uf= 1,20 W/(m2·K).
Jak widać, wartości badanych czynników, zapewniające maksymalną i minimalną wartości funkcji celu, lokują się na granicy obszaru czynnikowego, natomiast ekstrema badanej funkcji znajdują się daleko poza obszarem zmienności czynników.
Wnioski
W prezentowanym badaniu ukazana została wysoka skuteczność korzystania z modelowania matematycznego dla przeprowadzenia analizy parametrów cieplnych okien. Opracowany deterministyczny model matematyczny pozwolił dokładnie określić charakter i stopień wpływu podstawowych czynników w wybranym zakresie ich zmienności na współczynnik przenikania ciepła Uw stolarki okiennej.
Współczynnik Uw najszybciej wzrastał pod wpływem współczynnika przenikania ciepła powierzchni szklonej Ug. Wraz ze zmianą współczynnika Ug od 0,2 W/(m2·K) do 1,0 W/(m2·K) zaobserwowano równomierny wzrost wartości współczynnika Uw od 0,616 W/(m2·K) do 1,256 W/(m2·K).
Pozostałe czynniki charakteryzują się ujednoliconym słabym wpływem na współczynnik Uw w zakresie od 5,4% do 11,3%.
Parametr Uf wykazuje efekt dodatni, czyli wraz z jego wzrostem, rośnie także wartość współczynnika Uw, a parametry A0 i C wykazują efekty ujemne, czyli wraz z ich wzrostem wartość współczynnika Uw słabo maleje.
Współczynnik Uw osiąga wartość minimalną Uw,min = 0,480 W/(m2·K) przy następujących wartościach czynników:
- A0= 2,367 m2;
- C =0,95;
- Ug= 0,200 W/(m2·K);
- Uf = 0,700 W/(m2·K).
Wartość maksymalną Uw,max = 1,368 W/(m2·K) obserwuje się dla:
- A0= 1,274 m2;
- C = 0,65;
- Ug= 1,0 W/(m2·K);
- Uf=1,2 W/(m2·K).
Literatura
- Rozporządzenie Ministra Infrastruktury z dn. 12 kwietnia 2002 r. w sprawie warunków technicznych, jakim powinny odpowiadać budynki i ich usytuowanie z późniejszymi aktualizacjami.
- PN-EN ISO 12631:2013-03, "Cieplne właściwości użytkowe ścian osłonowych. Obliczanie współczynnika przenikania ciepła".
- PN-EN ISO 10077-1:2007 "Cieplne właściwości użytkowe okien, drzwi i żaluzji. Obliczanie współczynnika przenikania ciepła. Część 1: Metoda uproszczona".
- J. Gutenbaum, "Modelowanie matematyczne systemów", EXIT, Warszawa 2003.
- Z. Polański, "Planowanie doświadczeń w technice", PWN, Warszawa 1984.
- PN-EN 14351-1+A1:2010, "Okna i drzwi. Część 1: Okna i drzwi zewnętrzne bez właściwości dotyczących odporności ogniowej i/lub dymoszczelności".
- PN-EN ISO 14683:2008, "Mostki cieplne w budynkach. Liniowy współczynnik przenikania ciepła. Metody uproszczone i wartości orientacyjne".
- K. Hartmann, E. Lezki, W. Schär, "Statistische Versuchsplanung und -auswertung in der Stoffwirtschaft", VEB, 1977 Leipzig.
- W. Krysicki i in., "Rachunek prawdopodobieństwa i statystyka matematyczna w zadaniach. Część II. Statystyka matematyczna", PWN, Warszawa 2003.
PLIKI DO POBRANIA




![RYS. 2. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od współczynników przenikania ciepła szyby Ug [W/(m2·K)] i ramy okiennej Uf [W/(m2·K)] przy powierzchni okna A0=1820 m2 i udziale pola powierzchni płaszczyzny szklonej do .](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/analiza-parametrow-stolarki-okiennej-rys2.jpg)
![RYS. 3. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od powierzchni okna A0 [m2] i udziału pola powierzchni płaszczyzny szklonej do całkowitego pola powierzchni okna C przy współczynniku przenikania ciepła szyby Ug = 0,6 W/(.](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/analiza-parametrow-stolarki-okiennej-rys3.jpg)