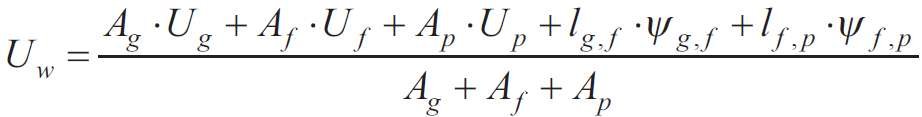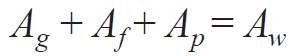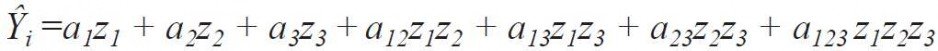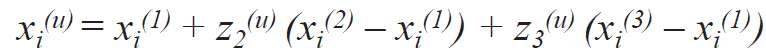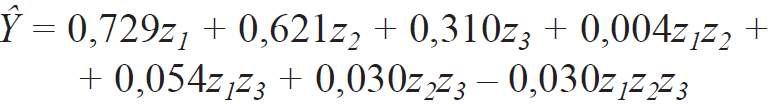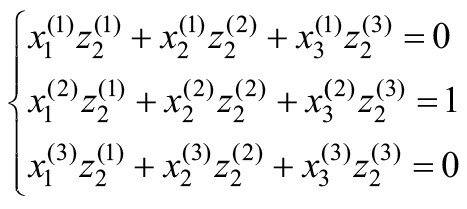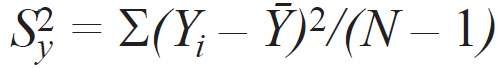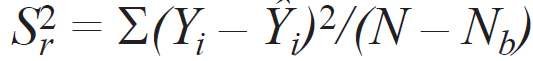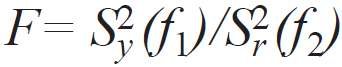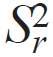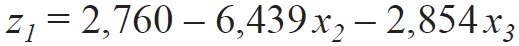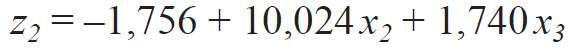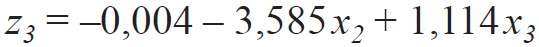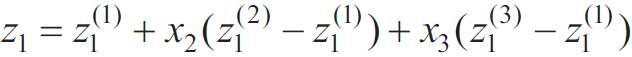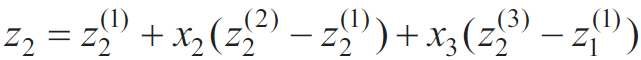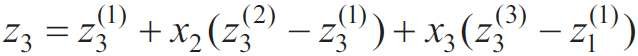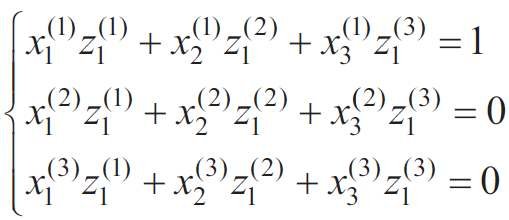Współczynnik przenikania ciepła ściany osłonowej z oknem
Model matematyczny z uwzględnieniem powierzchni elementów składowych

W artykule zaprezentowano podejście do opracowania modelu matematycznego współczynnika przenikania ciepła ściany osłonowej z oknem, wykonanym z PVC w budynku mieszkalnym...
Fot. Warbud
Ściany osłonowe w budynkach mieszkalnych chronią pomieszczenia przed oddziaływaniem czynników klimatycznych i najczęściej składają się z dwóch różnorodnych odcinków - muru oraz okna złożonego z ramy i oszklenia.
Zobacz także
Fiberglass Fabrics sp. z o.o. Tynki i farby w dużych inwestycjach budowlanych

Przy projektowaniu i realizacji dużych inwestycji, takich jak osiedla mieszkaniowe, biurowce czy obiekty użyteczności publicznej, kluczowe znaczenie ma wybór odpowiednich materiałów wykończeniowych. Nie...
Przy projektowaniu i realizacji dużych inwestycji, takich jak osiedla mieszkaniowe, biurowce czy obiekty użyteczności publicznej, kluczowe znaczenie ma wybór odpowiednich materiałów wykończeniowych. Nie do przecenienia jest rola tynków i farb, które wpływają na wygląd budynków, a także na ich trwałość i komfort użytkowania.
Connector.pl Nowoczesne piany poliuretanowe – szczelne i trwałe ocieplenie budynku

Firma Connector.pl to największy polski dystrybutor materiałów do produkcji kompozytów, będący liderem na rynku od ponad 30 lat. W swojej ofercie posiadamy szeroką gamę produktów, a wśród nich znakomitej...
Firma Connector.pl to największy polski dystrybutor materiałów do produkcji kompozytów, będący liderem na rynku od ponad 30 lat. W swojej ofercie posiadamy szeroką gamę produktów, a wśród nich znakomitej jakości piany PUR otwarto- i zamkniętokomórkowe.
Czytaj całość »
M.B. Market Ltd. Sp. z o.o. Czy piana poliuretanowa jest palna?
W artykule chcielibyśmy przyjrzeć się bliżej temu aspektowi i rozwiać wszelkie wątpliwości na temat palności pian poliuretanowych.
W artykule chcielibyśmy przyjrzeć się bliżej temu aspektowi i rozwiać wszelkie wątpliwości na temat palności pian poliuretanowych.
Czytaj całość »
ABSTRAKT |
|---|
|
W artykule zaprezentowano podejście do opracowania modelu matematycznego współczynnika przenikania ciepła ściany osłonowej z oknem, wykonanym z PVC w budynku mieszkalnym, w zależności od udziałów pól powierzchni elementów składowych (odcinków ściany pełnej, ramy okiennej i powierzchni szklonej). Przy realizacji eksperymentu obliczeniowego zastosowano lokalne planowanie sympleksowe w warunkach ograniczenia zakresu zmienności wybranych czynników. Analiza wykonana została na podstawie opracowanego deterministycznego modelu matematycznego opisującego tą zależność. Oszacowano efekty wpływu badanych czynników. Informacja może być przydatna dla naukowców, producentów i konsumentów stolarki okiennej. |
Mathematical model of the heat transfer coefficient for a curtain wall with a window, taking into account the surface areas of specific componentsThe article presents an approach to the development of a mathematical model of heat transfer coefficient for a curtain wall with a PVC window in a residential building, depending on the specific proportions of component surface areas (solid wall sections, window frames and glazed surfaces). In the course of implementation of the computational experiment, local simplex planning was used in the conditions of limited range of variability of selected factors. The analysis was made on the basis of the complete deterministic mathematical model describing this relationship. The effects of the studied factors were estimated. The information can be useful for scientists, producers and consumers of window joinery. |
Ściany osłonowe spełniają ważne role przy zapewnieniu komfortu cieplnego w pomieszczeniach oraz istotnie wpływają na zapotrzebowanie na energię do ogrzewania budynku. Odwołując się do wytycznych zawartych w Warunkach Technicznych [1], w Polsce od 1.01.2017 właściwości cieplne przegród w budynkach mieszkalnych ustalone zostały na poziomie:
- dla ścian zewnętrznych Umax = 0,23 W/(m2·K),
- dla okien Umax = 1,10 W/(m2·K)
oraz wprowadzono ograniczenie odnośnie pola powierzchni przegród przezroczystych w przypadku, gdy współczynnik przenikania ciepła Uw dla okna jest większy niż 0,9 W/(m2·K) [1].
Dobierając rozwiązanie ściany oraz rodzaj stolarki okiennej, należy porównywać ich parametry cieplne z powyższymi wartościami.
Niestety działanie to często ma charakter formalny, czasem jednak jest ono bezsensowne i nierealizowalne.
Wymagany poziom współczynnika przenikania ciepła można łatwo osiągać tylko przy projektowaniu i wykonaniu ścian budynków nowo wznoszonych. Można wówczas precyzyjnie dobrać odpowiednią grubość warstwy termoizolacyjnej, obniżającej końcową wartość współczynnika przenikania ciepła kompleksowej ściany osłonowej.
Dla współczesnej stolarki, która składa się z kilku elementów o deklarowanych przez producentów właściwościach cieplnych, dobór odpowiedniej wartości współczynnika U okna często jest problematyczny. Zdarza się, że producenci stolarki okiennej zatajają informacje na temat współczynnika przenikania ciepła dla całego okna.
Bezsensowność weryfikacji wartości współczynników przenikania ciepła elementów składowych związana jest z tym, że przy określeniu współczynnika U ściany osłonowej np. za pomocą metody składnikowej fragment przegrody dzieli się na pola powierzchni o różnych właściwościach cieplnych, a całkowity współczynnik przenikania ciepła oblicza się za pomocą ważonych powierzchniowo wartości U elementów składowych z dodatkowymi członami korekcyjnymi, uwzględniającymi wzajemne oddziaływania cieplne między tymi elementami [2].
Oznacza to, że przy zastosowaniu okna małych rozmiarów nie ma dużego znaczenia, czy jego współczynnik przenikania ciepła będzie mniejszy czy większy od wymaganego, ponieważ najmocniejszy wkład w poziom izolacyjności cieplnej wnosi ściana.
I na odwrót, przy zastosowaniu powierzchni szklonych wielokrotnie przeważających nad przegrodami pełnymi (tak zwanych przegród przezroczystych) nie ma istotnego znaczenia co do wyboru wartości współczynnika przenikania ciepła odcinka ściany pełnej, ponieważ wtedy najmocniejszy wkład w poziom izolacyjności cieplnej ściany osłonowej wnosi powierzchnia szklona.
Jednakże niezależnie od tego, przepisy mówią jasno, że nowo wznoszone budynki muszą charakteryzować się współczynnikiem przenikania ciepła poszczególnych elementów konstrukcyjnych na poziomie nie wyższym niż maksymalny dopuszczalny.
Zdaniem autorów niejednoznaczność sytuacji z unormowaniem elementów składowych ścian osłonowych z oknami może być wyeliminowana tylko po zamianie tradycyjnej weryfikacji wartości współczynników przenikania ciepła elementów składowych z wartościami wymaganymi na unormowanie właściwości cieplnych całej ściany osłonowej z oknami czy z przegrodami przezroczystymi. W tym celu autorzy proponują wprowadzenie kategoryzacji cieplnej ścian osłonowych. Jednak najpierw trzeba wykryć i oszacować stopień wpływu pól powierzchni elementów składowych oraz parametrów fizykalnych na całkowity współczynnik przenikania ciepła ścian osłonowych.
Celem danego badania jest opracowanie modelu matematycznego współczynnika przenikania ciepła ściany osłonowej z oknem wykonanym z PVC w budynku mieszkalnym w zależności od udziałów pól powierzchni elementów składowych oraz przeprowadzenie analizy na uzyskanym modelu matematycznym z oszacowaniem efektów wpływu czynników na właściwości cieplne badanej ściany.
Opis obiektu badania
Ściana osłonowa każdego pomieszczenia w budynkach mieszkalnych najczęściej jest fragmentem składającym się z odcinka ściany pełnej i okna.
Z uwzględnieniem nowych technologii montażu okien z PVC, dopuszczających szerokie możliwości zastosowania różnych rozwiązań ramy i różnorodnych typów oszklenia, z bardzo zróżnicowanymi cechami fizykalnymi w odniesieniu do ściany osłonowej jak i samego okna, jako obiekt badania dla dalszej analizy przyjęto fragment ściany z trzema elementami:
- ścianą pełną,
- ramą
- i powierzchnią szkloną.
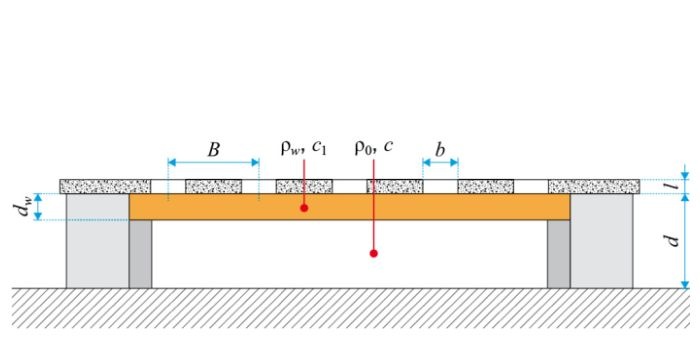
Schematy takiego fragmentu pokazano na RYS. 1.
Rozmiary fragmentu ściany uwzględniają rozwiązania przestrzenne pomieszczeń mieszkalnych i przyjęte zostały następująco:
2,80×3,60 m (wysokość×szerokość) = 10,08 m2.
W ramach tej wartości w badaniu zmieniały się różne kombinacje pól powierzchni okien, od rozmiaru 0,675×0,90 m = 0,608 m2 do 2,20×3,00 m = 6,60 m2.
Wysokość okna w analizowanym fragmencie przyjęto od wartości najmniejszej 0,675 m do charakterystycznej wysokości przegród przezroczystych wynoszącej niemal tyle, co wysokość pomieszczenia.
Lokalizacja okna przyjęta została w granicach badanego fragmentu ściany z zapewnieniem po obwodzie okna odcinków ściany o szerokości nie mniejszej niż 0,30 m.
Metoda obliczania współczynnika przenikania ciepła
Do obliczania współczynnika przenikania ciepła fragmentu ściany osłonowej z oknem przydatna i oczywista jest wspomniana wcześniej metoda składnikowa [2]. Według tej metody współczynnik przenikania ciepła Uw fragmentu ściany osłonowej z oknem należy obliczać według wzoru:
gdzie:
Ug, Uƒ, Up - współczynniki przenikania ciepła, odpowiednio: oszklenia, ramy, ściany pełnej,
ψg,ƒ, ψƒ,p - liniowe współczynniki przenikania ciepła spowodowane połączonymi efektami cieplnymi elementów, odpowiednio: szklącego i ramy, ramy i ściany pełnej,
lg,ƒ, lƒ,p - długość liniowego mostku cieplnego powstającego na styku, odpowiednio: szkła i ramy, ramy i ściany pełnej,
Ag, Aƒ, Ap, Aw - pole powierzchni, odpowiednio: oszklenia, ramy, ściany pełnej oraz fragmentu ściany osłonowej.
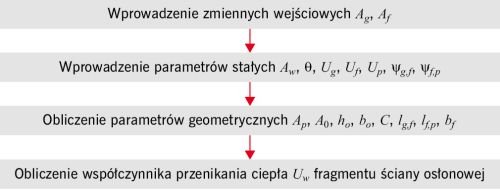
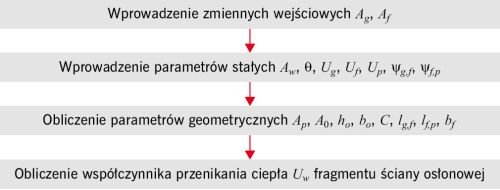
RYS. 2. Schemat blokowy obliczania współczynnika przenikania ciepła Uw fragmentu ściany osłonowej; rys. archiwa autorów
θ - proporcje okna, wyrażone stosunkiem ho/bo,
Ao = Ag + Aƒ - powierzchnia okna,
ho - wysokość okna,
bo - szerokość okna,
C - udział powierzchni szklonej do powierzchni okna,
bƒ - szerokość elementów ramy
Mimo prostego wyrazu wzór (1) jest bardzo złożoną zależnością dla przeprowadzenia analizy czynnikowej.
Nawet przy trzech elementach składowych wzór ten daje aż 10 czynników do przeanalizowania.
Każdy dodatkowy element składowy w zależności od lokalizacji zwiększa liczbę czynników od 4 do 6 parametrów.
Jednak najtrudniejszym zadaniem dla przeprowadzenia analizy był warunek, którym są powiązane trzy pierwsze zmienne:
Odnosząc się do przedstawionego wzoru (1), autorzy stworzyli algorytm do wyliczania szukanego współczynnika przenikania ciepła okna Uw przy zmianie wartości wybranych czynników ( RYS. 2 ). Ten algorytm posłużył jako podstawa do opracowania autorskiego programu komputerowego w Microsoft Excel.
Model matematyczny do określenia współczynnika przenoszenia ciepła
Wstępna analiza czynników pozwoliła wykryć, że oprócz zmiennych Ag, Aƒ, Ap oraz lg,ƒ, lƒ,p pozostałe zmienne są sterowalne, mierzalne, wzajemnie niezależne, niesprzeczne i odpowiadają podstawowym wymaganiom modelowania matematycznego [3].
Zmienne lg,ƒ, lƒ,p są zależne od Ag i Aƒ oraz niejednoznaczne.
Zapewnienie jednoznaczności lg,ƒ, lƒ,p możliwe jest poprzez przyjęcie wysokości okna jako wartości stałej lub poprzez wprowadzenie dodatkowego parametru θ charakteryzującego proporcje okna i wyrażonego stosunkiem ho/bo .
W niniejszym badaniu w celu zapewnienia jednoznaczności długości liniowych mostków cieplnych wprowadzono parametr θ , co pozwoliło zbadać wpływ udziałów powierzchni oszklenia i ramy na współczynnik Uw w znacznie większym zakresie ich zmienności.
Przy obliczeniach wartość parametru θ okien przyjęto równą 0,75, co jest bliskie proporcji samego fragmentu ściany.
Zgodnie z przyjętym celem badania, współczynnik przenikania ciepła Uw fragmentu ściany (funkcja celu Y ) postanowiono zbadać w zależności od trzech czynników geometrycznych: udziałów powierzchni szklonej (czynnik z1 ), powierzchni ramy (czynnik z2 ) i powierzchni ściany pełnej (czynnik z3 ). Pozostałe parametry przyjęto na stałym poziomie.
Ponieważ czynniki geometryczne z1, z2, z3 są związane warunkiem (2), to do zbadania ich wpływu zastosowano planowanie sympleksowe dla trzech zmiennych w układzie „skład–własność”, zawierającego N = 7 prób ( TABELA 1 ) [4].
To podejście tradycyjnie stosuje się do opisu właściwości mieszanek w zależności od składu komponentów.
Autorzy wykryli formalne podobieństwo do rozpatrywanego zagadnienia i podjęli próbę zastosowania go do rozwiązania zagadnienia z fizyki budowli.
Plan sympleksowy przewiduje określony układ realizacji obliczeń przy spełnieniu warunku z1+ z2 + z3 = 1 i opracowanie modelu w postaci niepełnego wielomianu trzeciego stopnia dla trzech zmiennych:
Przy wykonywaniu obliczeń, wartości parametrów stałych przejęto na poziomie współczesnych wymagań ochrony cieplnej:
Ug = 0,70 W/(m2·K),
Uƒ = 1,10 W/(m2·K),
Up = 0,23 W/(m2·K).
Wartości liniowych współczynników przenikania ciepła na granice szkło–rama oraz rama–ściana przyjęto jednakowe na poziomie 0,080 W/(m·K) [5].
Według planu ( TABELA 1 , kolumny 2-4) każdy z czynników z1, z2, z3 należy rozpatrywać na czterech poziomach:
a) 0,00
b) 0,333
c) 0,50
d) 1,00.
Ten warunek nie odpowiadał przyjętemu celowi, ponieważ nie miało sensu wykonywać badania w całym zakresie zmiany udziałów wybranych czynników (od 0 do 1).
Praktyczne znaczenie miały jedynie takie zakresy zmienności czynników, które odpowiadały realnym układam fragmentu ściany z oknem. W związku z tym w badaniu zastosowano lokalne planowanie sympleksowe w warunkach ograniczenia zakresu zmienności wszystkich czynników [6].
Na podstawie wstępnej analizy wybranego fragmentu ściany osłonowej został wybrany podobszar, obejmujący preferowane udziały elementów składowych:
- powierzchni szklonej (χ1) od 0,048 do 0,524,
- ramy (χ2) od 0,012 do 0,176,
- ściany (χ3) od 0,364 do 0,940.
Wartości udziałów składników określały współrzędne wierzchołków wybranego do badania podobszaru:
- A1 (χ1 = 0,524, χ2 = 0,112, χ3 = 0,364),
- A2 (χ1 = 0,254, χ2 = 0,176, χ3 = 0,570),
- A3 (χ1 = 0,048, χ2 = 0,012, χ3 = 0,940).
Wyżej wymieniony podobszar został transformowany do pełnego planu sympleksowego poprzez wprowadzenie pseudo składników z1, z2, z3 , które w każdym u-tym układzie planu są związane z czynnikami rzeczywistymi χ1, χ2, χ3 zależnością [6]:
Poziomy zmienności czynników z1, z2, z3 oraz odpowiadające im naturalne wartości χ1, χ2, χ3 przedstawiono w TABELI 1 (kolumny 2-6).
Po przeprowadzeniu niezbędnych obliczeń możliwie było opracowanie modeli badanej cechy w zależności od pseudo składników ( z1, z2, z3 ).
Chcąc otrzymać modele matematyczne z czynnikami w postaci naturalnej ( χ1, χ2, χ3 ), należało odkodować je przez podstawienie odpowiednich zależności.
Za pomocą wzorów, podanych w [4] opracowano zależności Y = ƒ ( z1, z2, z3 ):
Po określeniu współczynników równania regresji należało sprawdzić adekwatność opracowanego modelu (5). Ponieważ w eksperymencie obliczeniowym zastosowano plan nasycony i brakowało stopni swobody do przeprowadzenia tradycyjnej procedury testowania, to do oceny adekwatności wykonano obliczenia w dodatkowych (poza planem) dziewięciu punktach ( TABELA 2 ).
Z drugiej strony uwzględniono, że modele deterministyczne charakteryzują się wzajemnie jednoznaczną zgodnością pomiędzy oddziaływaniem zewnętrznym a reakcją na to oddziaływanie. Z tego powodu w każdym punkcie planu wykonano tylko jedno doświadczenie. Przy braku powtórzeń i wariancji niedokładności pomiarów, adekwatność uzyskanego równania można ocenić, porównując wariancje średniej oraz wariancję resztkową obliczonych według wzorów [7]:
gdzie:
N - liczba wykonanych obliczeń,
Nb - liczba współczynników w równaniu regresji.
Do testowania zastosowano kryterium Fiszera, który pokazuje, o ile razy zmniejsza się rozsiew odnośnie równania regresji w porównaniu z rozsiewem odnośnie średniego [7]:
gdzie:
ƒ1, ƒ2 - liczby stopni swobody,
ƒ1 = (N – 1) = 9 – 1 = 8;
ƒ2 = (N – Nb) = 9 – 7 = 2.
Równanie regresji opisuje wyniki obliczeń adekwatnie, jeżeli wartość F jest większa od wartości tabelarycznej Ft przy poziomie istotności p oraz stopniach swobody ƒ1 i ƒ2 .
Jak wynika z obliczeń:
F = 0,0061/0,000042 = 145,4967,
wartość tabelaryczna: Ft = F0,05; 8; 2 = 19,4 [7].
To że F wielokrotnie przekracza Ft , oznacza, że model jest adekwatny i przydatny do dalszej analizy. Jego wysoką jakość potwierdza również współczynnik determinacji R2 = 0,998.
W celu praktycznego zastosowania uzyskanych modeli może być wykonane odkodowanie przez podstawienie w nich zależności między naturalnymi wielkościami i pseudo składnikami. W tym celu opracowano formuły związku pomiędzy naturalnymi współrzędnymi χi a współrzędnymi zi .
Dla przeniesienia współrzędnych z jednego systemu afinicznego do drugiego zastosowano wzory z pracy [6]:
Ponieważ przeniesienie współrzędnych jest możliwe tylko dla niezależnych zmiennych, tj. niezwiązanych warunkiem (2), to równanie (5) należało przekształcić, pomijając jedną zmienną, np. z3 . Dlatego wartości zi(j) wyliczono poprzez rozwiązanie dwóch układów równań:
W wyniku rozwiązania układów równań (12) i (13) uzyskano wartości zi(j) i po podstawieniu ich w (9), (10) otrzymano formuły związku pomiędzy współrzędnymi naturalnymi χi a systemem współrzędnych zi :
Po podstawieniu zależności (14), (15), (16) do wzoru (5) można uzyskać równanie regresji w naturalnych współrzędnych. Jednak do interpretacji wyników badania zastosowano model (5). Ten model pozwolił badany podobszar powiększyć do pełnego trójkąta sympleksowego, znacznie ułatwiając interpretację wyników.
Analiza wyników badania
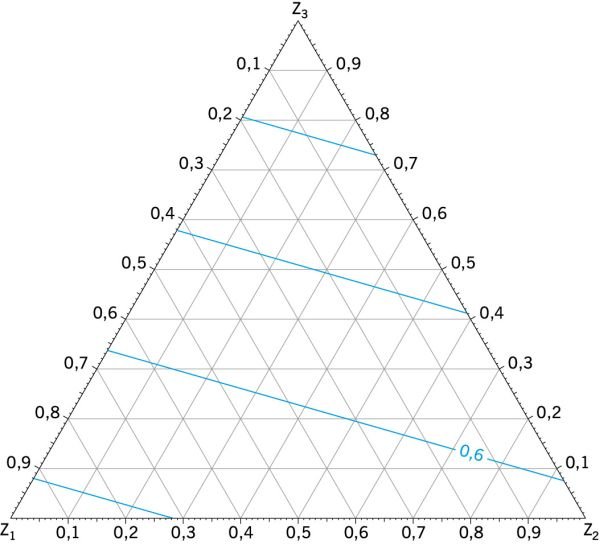
Do analizy wyników badania za pomocą modelu (5) opracowano wykres w postaci izolinii badanej zależności od rozpatrywanych czynników we współrzędnych pseudo składników z1, z2, z3 ( RYS. 3 ). Natomiast merytoryczną interpretację wykonano w oparciu o dane z TABELI 1 i TABELI 2, przy zastosowaniu naturalnych współrzędnych χ1, χ2, χ3 .
Jak widać z RYS. 3 :
- najwyższą wartość 0,729 W/(m2·K) współczynnika przenikania ciepła Y fragmentu ściany z oknem uzyskano w wierzchołku Z1(punkt 1) przy χ1 = 0,524, χ2 = 0,112, χ3 = 0,364 (TABELA 1),
- natomiast najniższą 0,310 W/(m2·K) w wierzchołku Z3 (punkt 3) przy χ1 = 0,048; χ2 = 0,012, χ3 = 0,940.
W sensie praktycznym oznacza to, że w badanym fragmencie zamiana okna z powierzchnią Ao3 = 0,674×0,898 = 0,605 m2 (co odpowiada pkt. 3) na okno z powierzchnią Ao1 = 2,193×2,924 = 6,411 m2 (co odpowiada pkt. 1) spowoduje wzrost współczynnika przenikania ciepła Y fragmentu ściany z oknem o 135,2%. Udział powierzchni ściany pełnej wtedy zmaleje od 0,94 do 0,364.
Dla wykrytych punktów ekstremalnych przeprowadzono symulację funkcji Y przy wahaniach na ±30% współczynników przenikania ciepła oszklenia, ramy oraz ściany pełnej.
Tak dla punktu 3 przy powierzchni okna Ao3 = 0,605 m2 wahania współczynnika Ug [0,490, 0,910 W/(m2·K)] powodują zmianę:
- funkcji Y odpowiednio do 0,300 i 0,320 W/(m2·K) (±3,2%),
- współczynnika Uf [0,770, 1,430 W/(m2·K)] - Y odpowiednio do 0,306 i 0,314 W/(m2·K) (±1,3%),
- współczynnika Up [0,161, 0,299 W/(m2·K)] - Y odpowiednio do 0,246 i 0,375 W/(m2·K) (±21,0%).
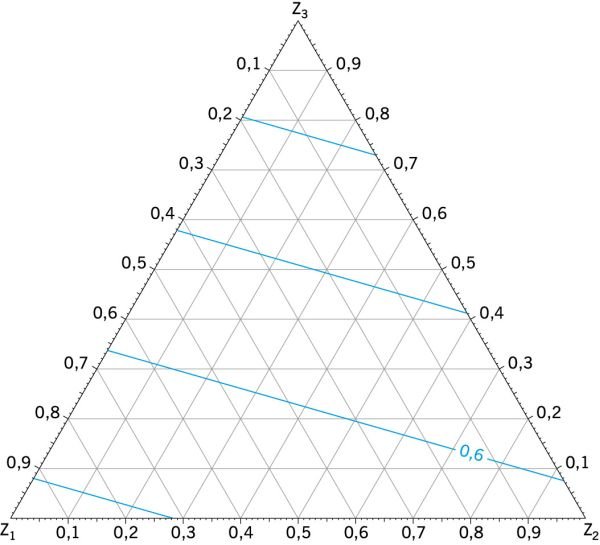
RYS. 3. Zależność współczynnika przenikania ciepła Y fragmentu ściany z oknem od udziałów elementów składowych: z1 - powierzchni oszklenia, z2 - powierzchni ramy, z3 - powierzchni ściany; rys. archiwum autorów (W. Jezierski, J. Borowska)
Podobna symulacja dla punktu 1 przy powierzchni okna Ao3 = 6,411 m2 wykryła inne zmiany Y .
Wahania:
- współczynnika Ug [0,490, 0,910 W/(m2·K)] dały wartości Y odpowiednio 0,619 i 0,839 W/(m2·K) (±15,1%),
- współczynnika Uf [0,770, 1,430 W/(m2·K)] - Y odpowiednio 0,692 i 0,766 W/(m2·K) (±5,1%),
- współczynnika Up [0,161, 0,299 W/(m2·K)] - Y odpowiednio 0,704 i 0,754 W/(m2·K) (±3,4%).
Wyniki tej symulacji wzmocniły przekonanie autorów odnośnie celowości zmiany w zakresie normowania przegród budowlanych - od weryfikacji do kategoryzacji.
Najmniejszy rozmiar okna Ao3 = 0,605 m2 został wybrany przez autorów w celu badawczym. Ale punktem odniesienia może być zastosowanie w tym samym fragmencie okna standardowego z powierzchnią Aos = 1,48×1,23 = 1,820 m2 [8].
Prowadzone poza planem obliczenia wykazały, że przy niezmiennych parametrach fizykalnych takie okno (przy udziale powierzchni szklonej 0,126, udziale powierzchni ramy 0,054) daje wartość współczynnika przenikania ciepła fragmentu ściany osłonowej z tym oknem Y = 0,416 W/(m2·K).
Według autorów wartość Uw = 0,416 W/(m2·K) może być przyjęta jako wartość graniczna dla ściany osłonowej z oknem pierwszej kategorii cieplnej.
Dla okna standardowego wahania:
- współczynnika Ug [0,490, 0,910 W/(m2·K)] dały wartości Y odpowiednio 0,389 i 0,442 W/(m2·K) (±6,3%),
- współczynnika Uf[0,770, 1,430 W/(m2·K)] - Y odpowiednio 0,398 i 0,434 W/(m2·K) (±4,3%),
- współczynnika Up [0,161; 0,299 W/(m2·K)] - Y odpowiednio 0,359 i 0,472 W/(m2·K) (±13,5%).
Wnioski
Opracowano model matematyczny zależności współczynnika przenikania ciepła fragmentu ściany osłonowej z oknem w budynku mieszkalnym od udziałów pól powierzchni oszklenia, ramy i ściany pełnej, za pomocą którego oszacowano efekty wpływu wybranych czynników.
Przy niezmiennych parametrach fizykalnych, wahania pól powierzchni oszklenia, ramy i ściany spowodowały wzrost współczynnika przenikania ciepła przyjętego do badania fragmentu o 135,2%.
Zmiana udziałów pól powierzchni oszklenia, ramy i ściany pełnej mocno koryguje wpływ współczynników przenikania ciepła elementów składowych na całkowity współczynnik przenikania ciepła fragmentu ściany z oknem.
Niniejszy artykuł ukazał się w miesięczniku IZOLACJE nr 1/2018 (s.50-54) pod tytułem „Model matematyczny współczynnika przenikania ciepła ściany osłonowej z oknem z uwzględnieniem powierzchni elementów składowych”
Literatura
- Obwieszczenie Ministra Infrastruktury i Rozwoju z dnia 17 lipca 2015 r. w sprawie ogłoszenia jednolitego tekstu rozporządzenia Ministra Infrastruktury w sprawie warunków technicznych, jakim powinny odpowiadać budynki i ich usytuowanie (DzU 2015, poz. 1422).
- PN-EN ISO 12631:2013-03, „Cieplne właściwości użytkowe ścian osłonowych. Obliczanie współczynnika przenikania ciepła”.
- J. Gutenbaum, „Modelowanie matematyczne systemów”, Wyd. EXIT, Warszawa 2003.
- V.Z. Brodskiy i in., „Tablicy planov eksperimenta dla faktornyh i polinomial’nyh modelej”, „Metalurgiâ”, Moskwa 1982.
- PN-EN ISO 14683:2008, „Mostki cieplne w budynkach. Liniowy współczynnik przenikania ciepła. Metody uproszczone i wartości orientacyjne”.
- I.G. Zedginidze, „Matematićeskoe planirovanie eksperymenta dla issledovaniâ i optimizacii svoistv smesej”, „Mecniereba” Tbilisi 1986.
- K. Hartmann, E. Lezki, W. Schär, „Statistische Versuchsplanung und – auswertung in der Stoffwirtschaft”, VEB, Leipzig 1977.
- PN-EN 14351-1+A2:2016-10, „Okna i drzwi cz. 1: Okna i drzwi zewnętrzne bez właściwości dotyczących odporności ogniowej i/lub dymoszczelności”.
PLIKI DO POBRANIA




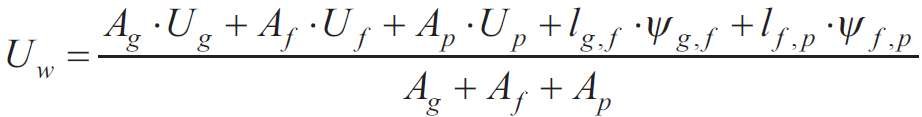
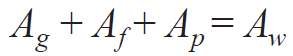
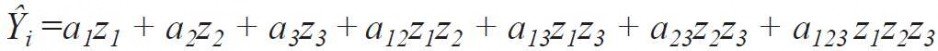
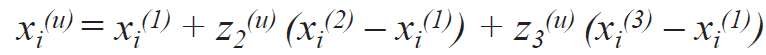
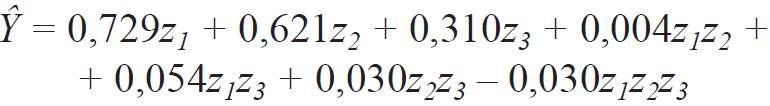
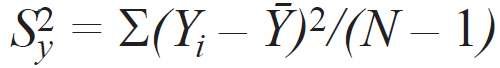
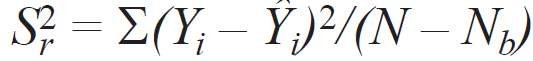
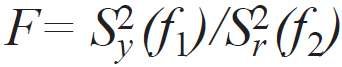
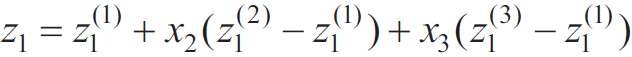
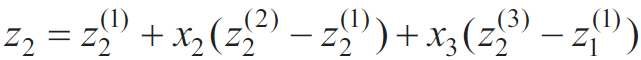
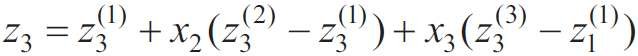
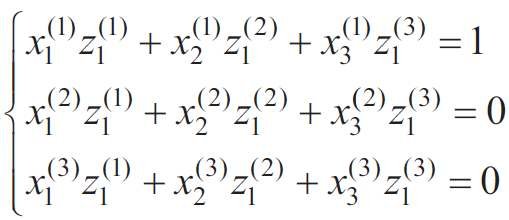
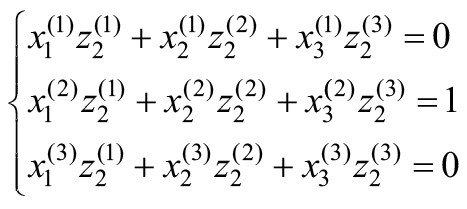
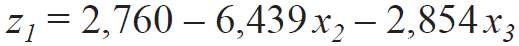
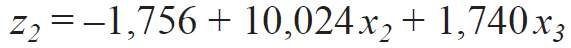
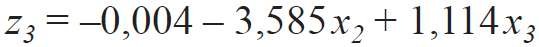

![TABELA 1. Plan eksperymentu, gdzie z1, z2, z3 – kodowane wartości czynników; x1, x2, x3 – naturalne wartości czynników (w liczniku – udziały, w mianowniku – powierzchnie, [m2]); Yi – wyniki obliczeń współczynnika przenikania ciepła fragmentu ściany osłon.](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/tabela1-1.jpg)
![TABELA 2. Wyniki obliczeń współczynnika przenikania ciepła fragmentu ściany osłonowej do oceny adekwatności modelu: gdzie x1, x2, x3 – naturalne wartości czynników
(w liczniku – udziały, w mianowniku – powierzchnie, [m2]); Yi – wyniki obliczeń, Ȳ – wart.](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/tabela2-1.jpg)