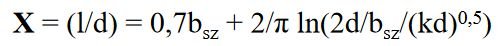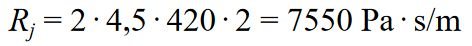Propozycja modyfikacji projektowania rezonansowych układów pochłaniających
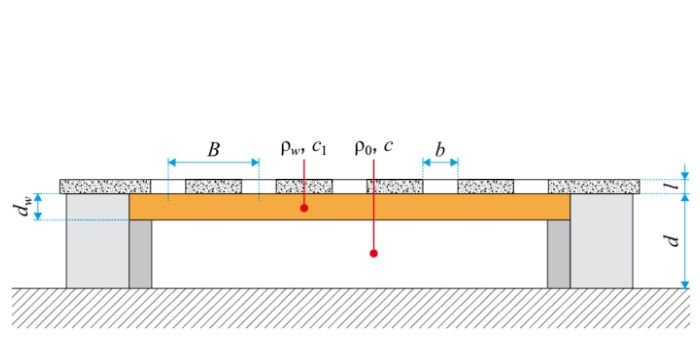
Szkic rozwiązania rezonansowego komorowego układu pochłaniającego, rys. G. Brzózka
Podstawy do projektowania rezonansowych układów pochłaniających zostały zaproponowane w odniesieniu do rezonatorów komorowych perforowanych i szczelinowych przez Smithsa i Kostena już w 1951 r. [1]. Jej szeroką interpretację w polskiej literaturze przedstawili profesorowie Sadowski i Żyszkowski [2, 3]. Pewną uciążliwość tej propozycji stanowiła konieczność korzystania z nomogramów, co determinuje stosunkowo małą dokładność.
Zobacz także
dr inż. Magda Kosmal, dr inż. Anna Kuśnierz Badanie izolacyjności akustycznej od dźwięków powietrznych szyb ognioodpornych

Obiekty budowlane (oraz ich poszczególne części), przy użytkowaniu ich zgodnie z zamierzonym zastosowaniem, muszą spełniać przez okres użytkowania szereg wymagań podstawowych. Należą do nich bezpieczeństwo...
Obiekty budowlane (oraz ich poszczególne części), przy użytkowaniu ich zgodnie z zamierzonym zastosowaniem, muszą spełniać przez okres użytkowania szereg wymagań podstawowych. Należą do nich bezpieczeństwo pożarowe oraz ochrona przed hałasem. Niezwykle istotne jest również wymaganie dotyczące zrównoważonego wykorzystania zasobów naturalnych. Wymagania te są podstawą do opracowywania norm i zharmonizowanych specyfikacji technicznych, w których określane są cechy wyrobów (zasadnicze charakterystyki)...
dr inż. Artur Nowoświat , dr inż. Leszek Dulak Wpływ zanieczyszczenia paneli dźwiękochłonnych na ich własności akustyczne

W niniejszym artykule autorzy przedstawiają wyniki badań, dotyczące wpływu stopnia zanieczyszczenia perforowanych paneli dźwiękochłonnych pyłem cementowym na wybrane parametry akustyczne.
W niniejszym artykule autorzy przedstawiają wyniki badań, dotyczące wpływu stopnia zanieczyszczenia perforowanych paneli dźwiękochłonnych pyłem cementowym na wybrane parametry akustyczne.
Iwona Sobczak Normy akustyczne w budownictwie

Normy akustyczne w budownictwie, takie jak PN-B-02151-4:2015-06 [1], nie powstały bez powodu. Skutki ekspozycji na hałas nie są natychmiastowe, ale za to bardzo poważne. Narażenie na głośne dźwięki może...
Normy akustyczne w budownictwie, takie jak PN-B-02151-4:2015-06 [1], nie powstały bez powodu. Skutki ekspozycji na hałas nie są natychmiastowe, ale za to bardzo poważne. Narażenie na głośne dźwięki może prowadzić do trwałego uszkodzenia słuchu, ale nie wolno też zapominać o znacznie powszechniejszym zagrożeniu – mianowicie pozasłuchowym wpływie hałasu na zdrowie. Będąc silnym stresorem, jest przyczyną m.in. zaburzeń snu, przyspieszonego zmęczenia, rozdrażnienia, kłopotów z koncentracją, a nawet chorób...
*****
Artykuł dotyczy metody projektowania rezonansowych układów pochłaniających zaproponowanej przez prof. A. Dobruckiego. Zaprezentowano inną procedurę obliczeniową. Ta metoda projektowania może być bardziej użyteczna z punktu widzenia praktyki inżynierskiej i wyklucza ewentualne błędy obliczeniowe wynikające z zastosowania algorytmu obliczeniowego zaproponowanego przez prof. A. Dobruckiego.
Proposal for modification of the design of resonance absorbing systems
The article focuses on the design method of resonance absorbing systems proposed by prof. A. Dobrucki. A different calculation method was proposed. This design method may be more useful from the point of view of engineering practice and excludes computational errors resulting from the application of the computational algorithm proposed by prof. A. Dobrucki.
*****
Uciążliwości te miały zostać wyeliminowane poprzez zastosowanie algorytmu obliczeniowego w opracowaniu [4], pozwalające na dostosowanie metodyki obliczeń do nowoczesnej techniki obliczeniowej. Weryfikacja tego algorytmu wskazuje na możliwość występowania w nim błędów. Dlatego podjęto próbę jego skorygowania.
Weryfikacja algorytmu obliczeniowego wg prof. Dobruckiego
Ponieważ opracowania, na które się powołuję, mogą być trudno dostępne, dlatego poniżej w skrócie przybliżam ich treść.
Algorytm prof. Dobruckiego
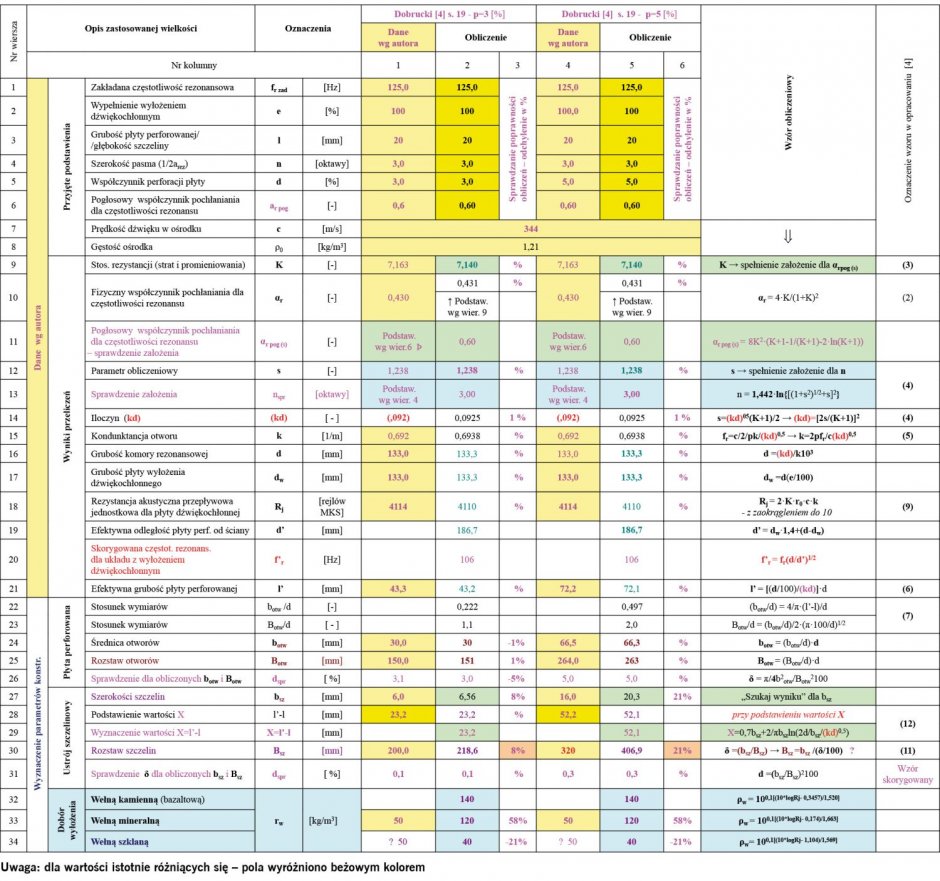
TABELA 1. Przykładowe przeliczenia rezonansowego komorowego układu pochłaniającego wg algorytmu zaproponowanego przez prof. Dobruckiego
Procedurę obliczeniową wg tego algorytmu opisano w opracowaniu [4], wykorzystano do przeprowadzenia obliczeń weryfikacyjnych w TABELI 1.
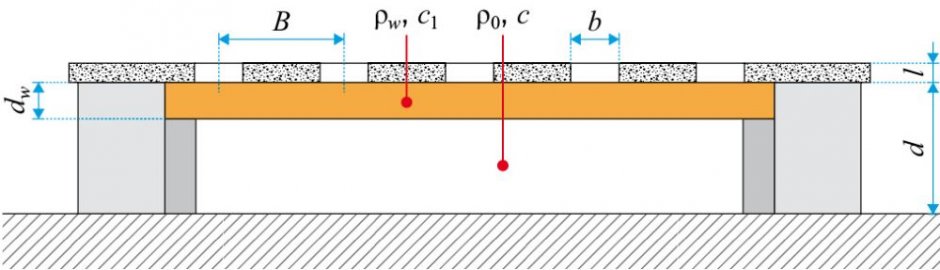
RYS. 1. Szkic rozwiązania rezonansowego komorowego układu pochłaniającego. Objaśnienia: ρw i ρ0 – gęstości wyłożenia dźwiękochłonnego i powietrza, c1 i c – prędkości rozprzestrzeniania się dźwięku w materiale wyłożenia dźwiękochłonnego i powietrzu, b i B – wymiary otworów bądź szczelin; odległości rozmieszczenia otworów lub szczelin, dw i d – grubość wyłożenia dźwiękochłonnego; grubość komory rezonansowej; rys.: G. Brzózka
W celu zrozumienia tego przykładu obliczeniowego w tabeli podano stosowane w tym opracowaniu wzory obliczeniowe wraz z ich numeracją – jak w cytowanym opracowaniu. Przedstawione przykłady bazują na przykładzie przedstawionym w tym opracowaniu, dla rezonansowego układu pochłaniającego jak na RYS. 1.
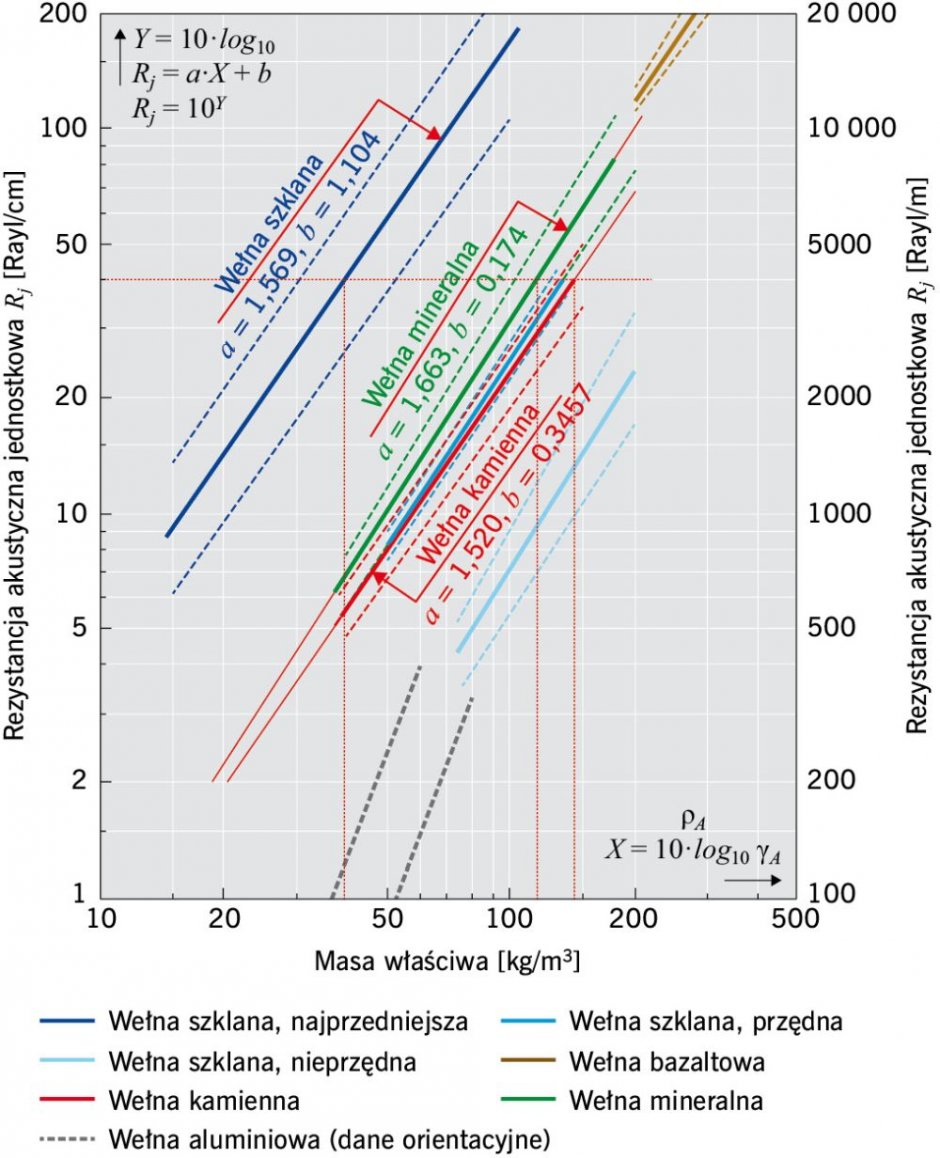
RYS. 2. Rezystancja akustyczna jednostkowa Rj ważniejszych materiałów dźwiękochłonnych; rys.: G. Brzózka
W odniesieniu do wyznaczenia gęstości materiału wyłożenia dźwiękochłonnego wykorzystano zależność rezystancji akustycznej jednostkowej tego materiału Rj od jego gęstości ρw, podanej w opracowaniu [5]. W przykładach obliczeniowych autor miał prawdopodobnie na myśli wełnę szklaną. Wartość 40 kg/m3 dotyczy dolnego przedziału odczytu tej wielkości z RYS. 2.
Opis procedury obliczeniowej w skondensowanej formie ujęto w opracowaniu [4] w formie przykładu obliczeniowego zacytowanego poniżej:
„Zaprojektujmy układ rezonansowy o następujących parametrach:
-
- częstotliwość rezonansowa ƒr = 125 Hz,
- pogłosowy współczynnik pochłaniania w rezonansie αrez = 0,6,
- liczba oktaw z tłumieniem nie mniejszym niż połowa rezonansowego n = 3,
- współczynnik perforacji δ = 3% lub 5%,
- grubość deski panelu l = 2 cm.
Ustalamy wartość fizycznego współczynnika pochłaniania w rezonansie αr = 0,43 oraz współczynnik rezystancji K = 7,163.
Następnie ze wzoru (4) obliczamy wartość s = 1,238 oraz iloczyn kd = 0,092.
Z kolei ze wzoru (5) oblicza się wartość k = 0,692 m oraz odległość panelu od ściany d = 0,133 m. Wielkość l’ = 4,33 cm dla współczynnika perforacji 3% oraz l’ = 7,22 cm dla δ = 5%.
Materiał wypełniający szczelinę na podstawie wzoru (9) ma oporność przepływową 4114 rejli/m, co może być uzyskane przez zastosowanie waty lub rzadkiej wełny mineralnej o gęstości 50 kg/m3.
W przypadku ustroju perforowanego, ze wzoru (7) uzyskuje się dla δ = 3% średnicę perforacji b = 3 cm oraz szerokość panelu B = 15 cm, zaś dla δ = 5% otrzymuje się wartości b = 6,65 cm oraz B = 26,4 cm. Wydaje się, że zgrabniejsza będzie boazeria ze współczynnikiem perforacji 3%.
Dla ustroju szczelinowego, z równania (12) oblicza się dla współczynnika perforacji 3% wartość szerokości szczeliny b = 0,6 cm i wartość szerokości panelu B = 20 cm. Dla współczynnika perforacji równego 5% odpowiednie wartości wynoszą: b = 1,6 cm oraz B = 32 cm. W tym przypadku korzystniej będzie wybrać rozwiązanie ze współczynnikiem δ = 5%.”
Wg tej procedury przeprowadzono obliczenia prezentowane w TABELI 1.
Dane wejściowe i wyniki obliczeń podane przez autora opracowania wyróżniono kolorem żółtym. Podobnie oznaczone dane wejściowe przyjęte do obliczeń weryfikacyjnych (2 kolumna i 4) wg procedury w [4] – pokrywające się z danymi wg autora.
W przypadku złożonych wzorów przeprowadzono obliczenia, wykorzystując na pasku Narzędzi w programie Excela procedurę obliczeniową „Szukaj wyniku”. Rezultaty takich przeliczeń wyróżniono kolorem zielonym lub jasnoniebieskim.
Uzupełniająco sprawdzano odchylenie procentowe pomiędzy wynikami obliczeń i danymi podanymi przez autora (3 kolumna i 6). Dla wartości znacznie różniących się pola wyróżniono beżowym kolorem.
W odniesieniu do obliczeń dla przykładu w TABELI 1, wyznaczone wyniki parametrów geometrycznych dla ustrojów szczelinowych odbiegają wyraźnie od podanych jako wzorcowe przez prof. Dobruckiego, jak również od odczytywanych z nomogramu Smithsa i Kostena. Jest to prawdopodobnie spowodowane błędem we wzorze (12) – do określenia szerokości szczelin:
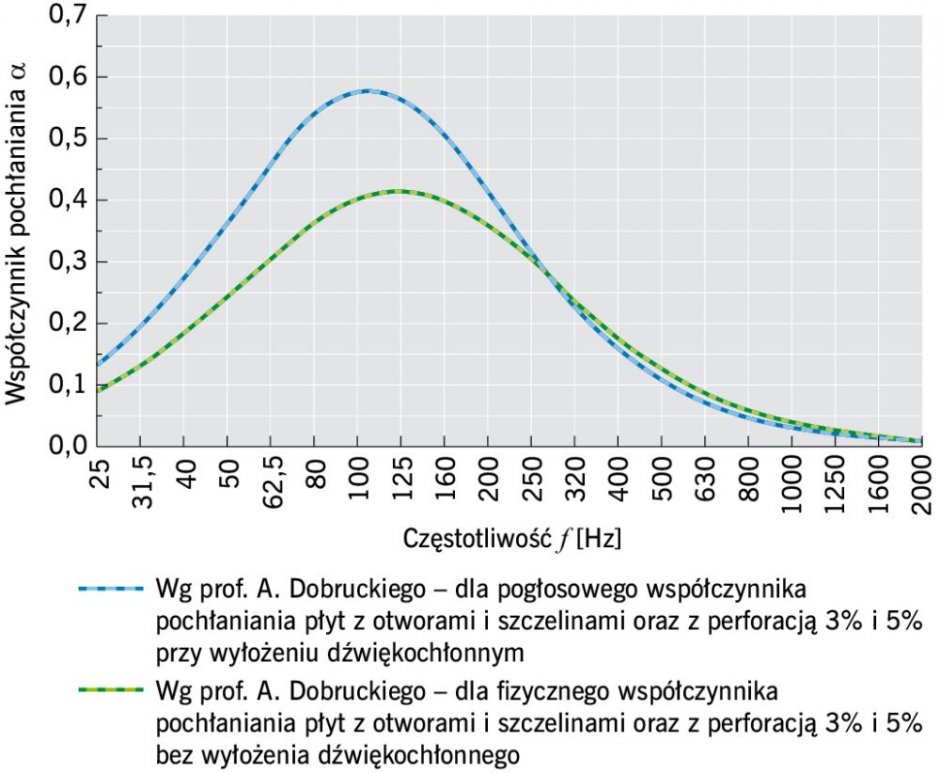
RYS. 3. Przebiegi współczynników pochłaniania wyznaczonych z powyższych obliczeń (dla przypadków zastosowania wyłożenia dźwiękochłonnego); rys.: G. Brzózka
Na RYS. 3 zilustrowano przebiegi współczynników pochłaniania wyznaczonych z powyższych obliczeń.
Wyznaczone przebiegi współczynników pochłaniania dla perforacji 3% oraz 5% wzajemnie się pokrywają, ponieważ takie przyjęto założenie do obliczeń i dla takiego założenia obliczano dobór parametrów konstrukcyjnych.
Warto również zwrócić uwagę na znaczny przyrost wartości dla współczynników pogłosowych (praktycznie dotyczących warunków, jakie występują w pomieszczeniach) w odniesieniu do fizycznych oraz na zmniejszenie częstotliwości rezonansowej w przypadkach zastosowania wyłożenia dźwiękochłonnego.
Metoda proponowana przez Smithsa i Kostena
Wykorzystano do tego celu interpretacje przedstawione w opracowaniach [2, 3]. Projektowanie oparte jest na wykorzystaniu nomogramów – RYS. 4–6.
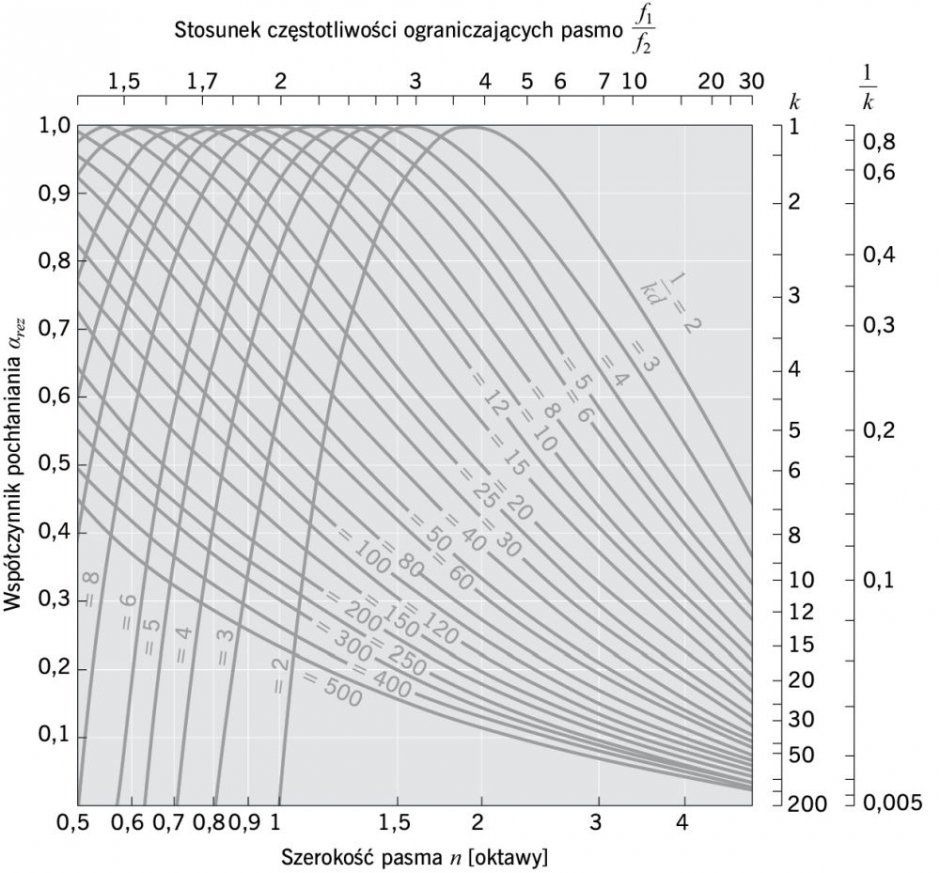
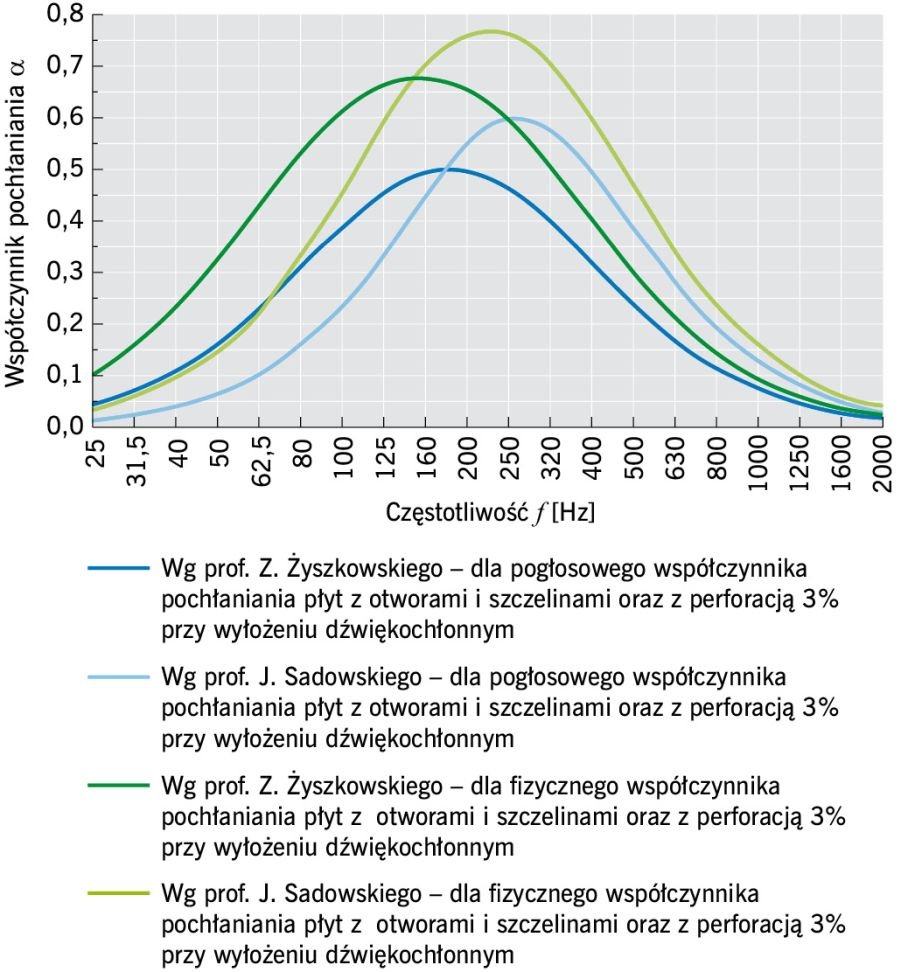
RYS. 4. Związek między współczynnikiem pochłaniania dźwięku przy rezonansie αrez, szerokością pasma n (w oktawach), wewnątrz którego współczynnik pochłaniania nie maleje poniżej αrez/2, stosunkiem rezystancji strat rezonatora do rezystancji promieniowania otworu rezonatora k i wielkością 1/kd; rys.: lewa strona wg rys. nr 20.17 z [3] i prawa strona wg rys. 17.8 z [2]
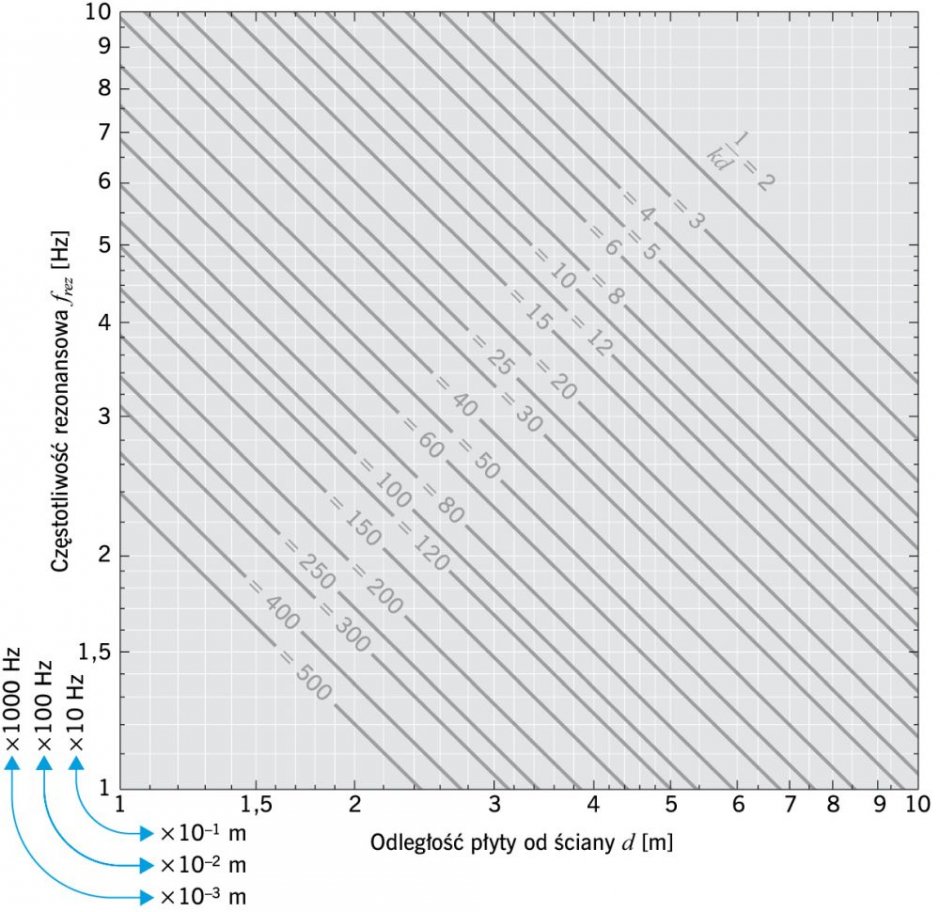
RYS. 5. Związek między częstotliwością rezonansową frez, odległością płyty od ściany d i wielkością 1/kd; rys.: lewa strona wg rys. nr 20.17 z [3] i prawa strona wg rys. 17.8 z [2]
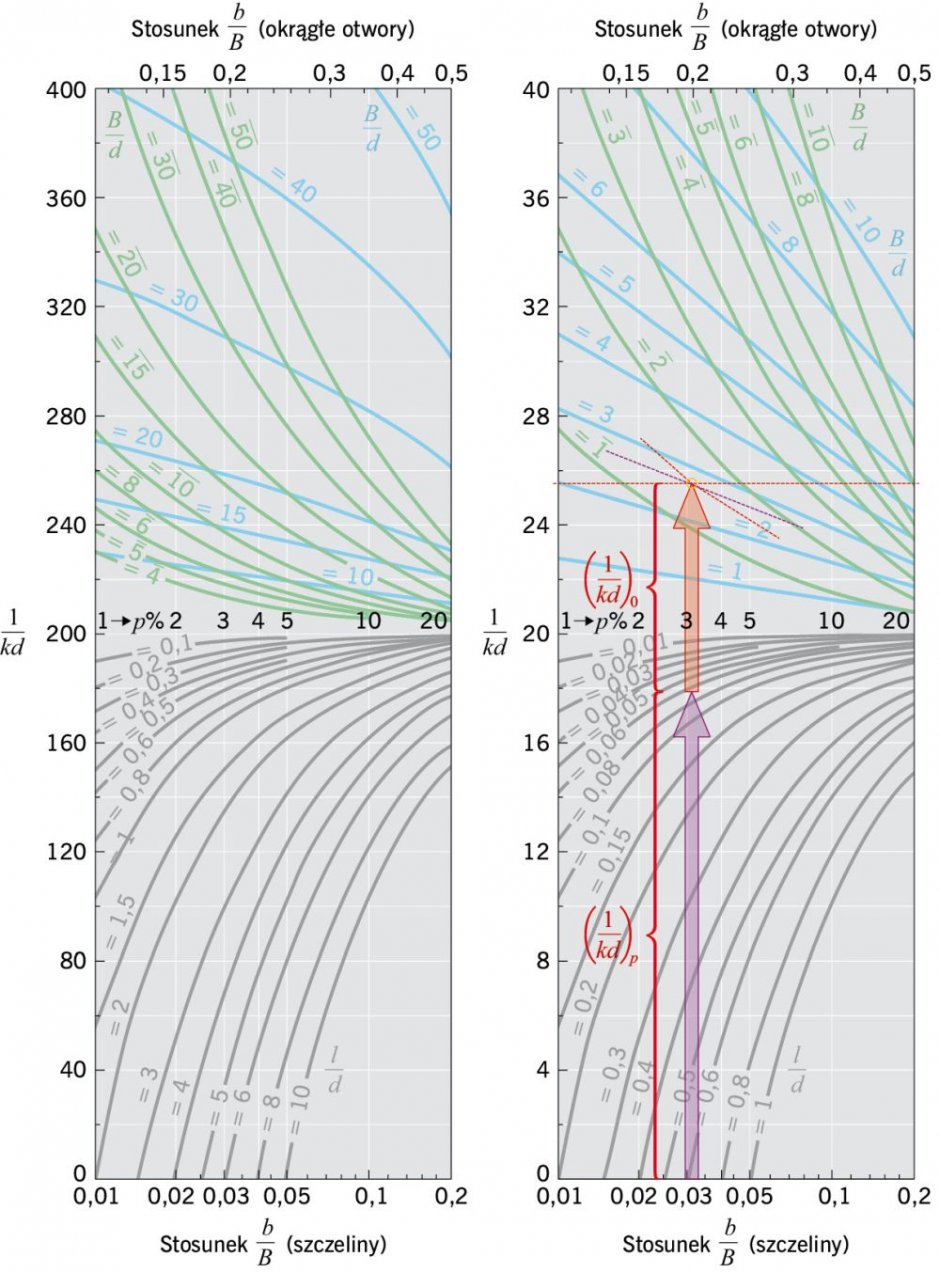
RYS. 6. Związek między wielkością 1/kd, współczynnikiem perforacji p oraz stosunkami B/d, l/d i b/B dla otworów okrągłych i szczelin; rys.: lewa strona wg [3] i prawa strona wg [2]
W opracowaniu cytowane są nomogramy wg prof. Żyszkowskiego [3]. Z prawej strony każdego z nomogramów podano odpowiadający im nr rysunku wg prof. Sadowskiego [2].
Cytowane przykłady obliczeniowe, które będą uwzględnione w dalszej części opracowania, wykonano zgodnie z cytowanymi poniżej skrótowymi opisami procedury:
- wg prof. Sadowskiego [2]:
Przykład 17-2. Obliczyć ustrój perforowany dla ƒr = 200 Hz, αrez = 0,5, n = 3 oktawy.
Z RYS. 4 znajduje się 1/kd = 8, a z RYS. 5 otrzymuje się d = 0,09 m.
Zakładając współczynnik perforacji p = 3% oraz otwory kołowe otrzymuje się z RYS. 6 wartości:
b/B = 0,195;
l/d = 0,08: (l ≈ 0,08 · 9 ≈ 7);
B/d = 1,4 (B ≈ 13 cm) oraz
b = 0,195 · 13 = 2,5 cm.
Wymaganą oporność przepływową materiału dźwiękochłonnego określa się z RYS. 4, znajdując K = 5,8, a następnie k = 1/(8 · 0,09) ≈ 1,4 (ρ0c = 420 raylów). Stąd R = 2 · 5,8 · 420 · 1,4 = 6280 raylów, co odpowiada akustycznej jednostkowej oporności przepływowej maty szklanej.
Obliczone fizyczne współczynniki pochłaniania dźwięku α0 mogą być zamienione na pogłosowe za pośrednictwem wykresu podanego na rys. 1-30 (uzyskane wartości α będą jedynie orientacyjne).
- wg prof. Żyszkowskiego [3]:
Przykład 2. Należy obliczyć ustrój z płytą perforowaną dla następujących wartości: ƒrez = 300 Hz, αrez = 0,6, n = 2,5 oktawy.
Z RYS. 4 otrzymuje się 1/kd = 8, a z RYS. 5 d = 0,061 m = 6,1 cm.
Przyjmując współczynnik perforacji p = 3% oraz otwory kołowe, z RYS. 6B otrzymuje się b/B = 0,195; zakładając dalej l/d = 0,08; (l ≈ 0,08 · 6,1 ≈ 0,5 cm) znajduje się w górnej części rysunku w odległości 1/kd = 8 B/d = 1,4; (B = 8,5 cm) i wreszcie b = 0,195 · 8,5 ≈ 1,7 cm.
Wymaganą rezystencję przepływową materiału wypełniającego komorę określimy, znajdując najpierw z RYS. 4 k = 4,5, a następnie k = 1/8 · 0,061 ≈ 2; (ρ0c = 420 Pa · s/m)
Wartość ta odpowiada rezystancji akustycznej jednostkowej przepływowej średnio gęstej waty żużlowej lub szklanej.
Dla tych przykładów zostały przeprowadzone obliczenia weryfikacyjne wg algorytmu [4], których rezultaty przedstawiono w TABELI 2.
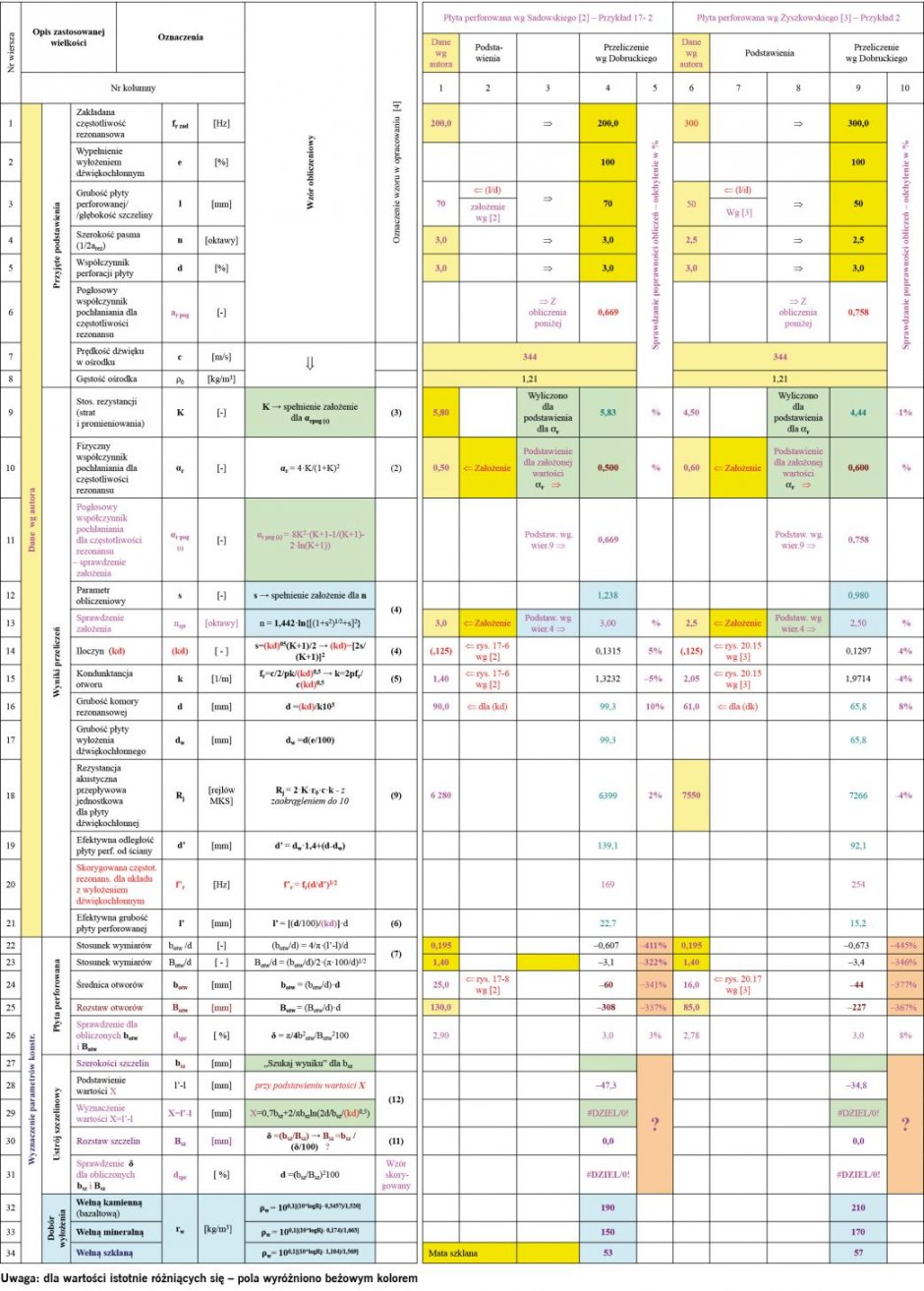
TABELA 2. Przykładowe przeliczenia rezonansowego komorowego układu pochłaniającego dla przykładów zaprezentowanych w opracowaniach prof. Sadowskiego i Żyszkowskiego
Dane wejściowe i wyniki obliczeń podane przez autora opracowania, dane wejściowe przyjęte do obliczeń weryfikacyjnych (1 i 6 kolumna) wg procedury w [4] – pokrywające się z danymi wg autora oraz rezultaty przeliczeń procedurą „Szukaj wyniku”, wyróżniono analogicznymi kolorami jak w TABELI 1.
Odpowiednio w kolumnach 2 i 3 oraz 7 i 8 każdego przykładu obliczeniowego przedstawiono symboliczne informacje, na jakiej podstawie określono dane. I dalej w kolumnach 5 i 10 sprawdzano odchylenie procentowe pomiędzy wynikami obliczeń a danymi podanymi przez autora.
Z przeglądu uzyskanych wyników dla przykładu w TABELI 2 wynika, że uzyskane parametry geometryczne dla ustrojów perforowanych i szczelinowych różnią się znacznie do podanych przez autora i odczytywanych z nomogramu Smithsa i Kostena lub są nierealne.
Z powyższego wynika oczywisty wniosek, że podany przez prof. Dobruckiego algorytm obliczeniowy jest niedokładny i nie weryfikuje wyników wzorcowych. Jest to prawdopodobnie spowodowane błędem we wzorze (6) na efektywną grubość płyty perforowanej l’ oraz (11) dotyczącym również obliczenia wskaźnika perforacji dla ustroju szczelinowego, który sformułowano jako: δ = bsz/Bsz, co jest niezgodne z przyjętymi założeniami podanymi pod (6), gdzie δ określono jako: „stosunek powierzchni otworów do powierzchni panelu”, co dla otworów w formie szczeliny można zdefiniować wzorem: δ = (bsz/Bsz)2.
Propozycja modyfikacji procedury obliczeniowej
Szczegółowa analiza wskazuje, że w algorytmie obliczeniowym prof. Dobruckiego [4] błędna jest jedynie procedura obliczeniowa dotycząca wyznaczania parametrów geometrycznych perforacji bądź rozstawień w ustroju szczelinowym. Pozostałe obliczenia ze sobą korespondują w przedziale dokładności odczytów z nomogramów. Dlatego proponuje się modyfikację procedury obliczeniowej wg [4], polegającą na:
- wykorzystaniu algorytmów obliczeniowych wg prof. Dobruckiego do obliczenia wszystkich uwzględnianych wielkości pomocniczych poza wyznaczeniem: efektywnej grubości płyty perforowanej l’ wg wzoru (6) i wyznaczeniem parametrów konstrukcyjnych ustrojów rezonansowych;
- wyznaczeniu parametrów konstrukcyjnych ustrojów rezonansowych wg nomogramu Smithsa i Kostena [1], zilustrowanego na RYS. 6.
Przykłady wykonania takich obliczeń dla danych z powyższych publikacji przedstawiono w TABELACH 3–4.
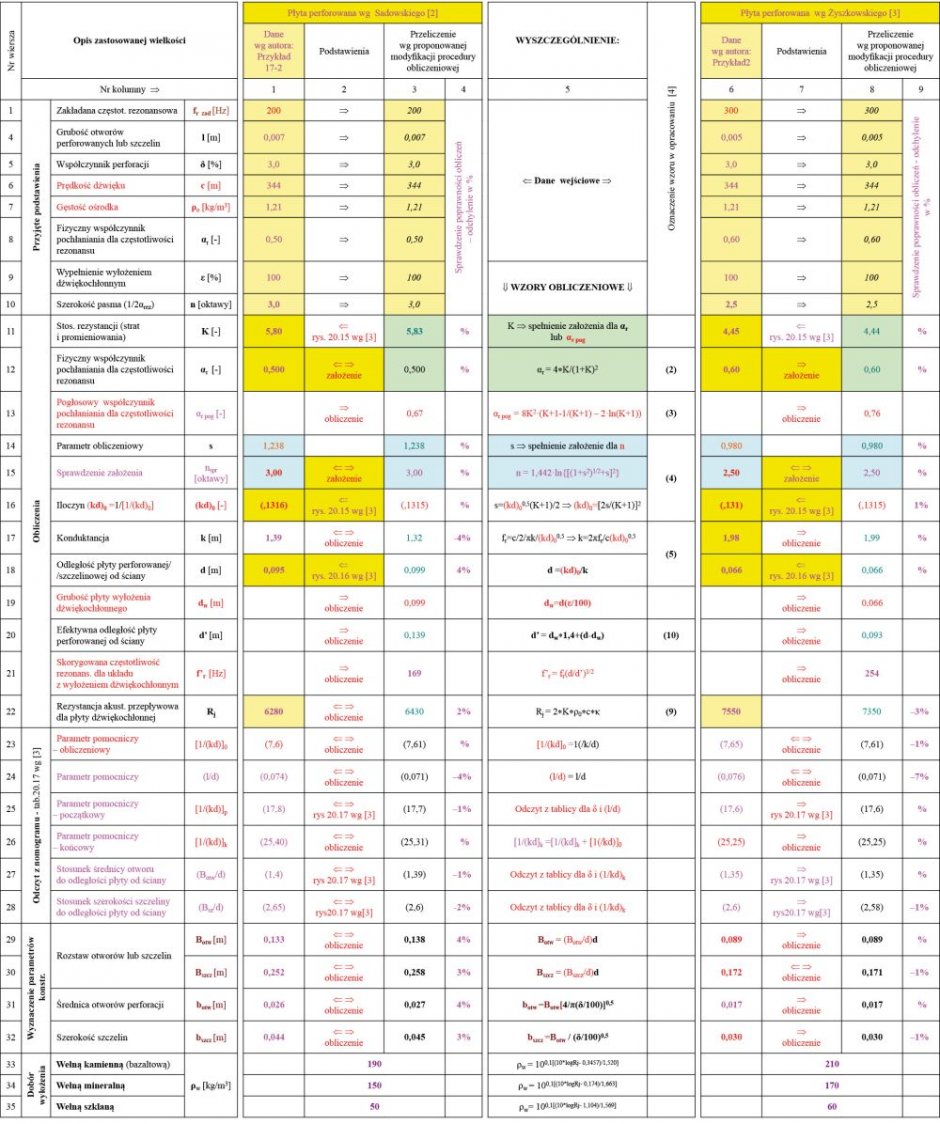
TABELA 3. Przykładowe przeliczenia rezonansowego komorowego układu pochłaniającego dla przykładów zaprezentowanych w opracowaniach prof. Sadowskiego i Żyszkowskiego według proponowanej modyfikacji obliczeń
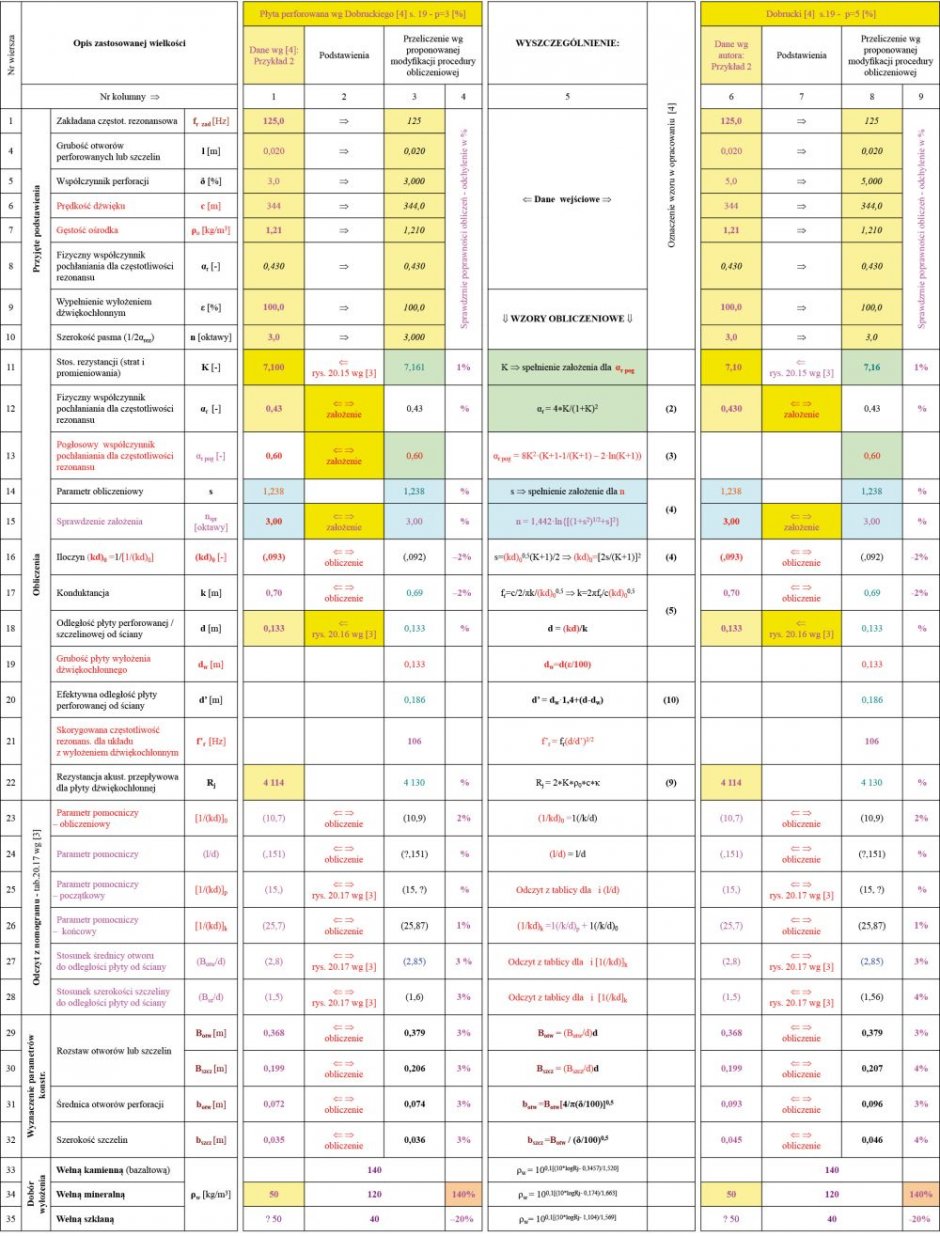
TABELA 4. Przykładowe przeliczenia rezonansowego komorowego układu pochłaniającego dla przykładów zaprezentowanych w opracowaniach prof. Dobruckiego według proponowanej modyfikacji obliczeń
Na RYS. 7 zilustrowano przebiegi współczynników pochłaniania wyznaczone w tych obliczeniach dla danych jak w TABELI 3.
Obliczenia (wiersze: 11–22) w kolumnach 3 i 8 wykonano wg algorytmów opisanych w kolumnie 5. Natomiast dane wg autora analizowanego przykładu obliczeniowego w kolumnach: 1 i 6. W kolumnach 2 i 7 zasygnalizowano te pozycje, których autorzy skorzystali z odczytów nomogramów.
Odczyty i obliczenia – wg cytowanych algorytmów – do wyznaczenia paramentów konstrukcyjnych ustrojów dźwiękochłonnych (wiersze 23–32) wykonano zgodnie z procedurą podaną w opracowaniach [2, 3] (nie cytowano danych podanych przez autorów). Odczyty te wykonano ze zwiększoną dokładnością w odniesieniu do podanych w powyższych opracowaniach.
Przeprowadzenie odczytu z nomogramu dla tych przykładów zilustrowano na rys. 20.17 wg [3].
Do wyznaczenia gęstości podstawowych trzech typów wypełnień dźwiękochłonnych wykorzystano opracowane przez autora niniejszego opracowania wzorów aproksymacyjnych na podstawie nomogramu jak na RYS. 2 (wiersze 33–35).
Uzyskane wyniki obliczeniowe dobrze ze sobą korespondują, a odchylenia pomiędzy danymi autorów i obliczeń nie przekraczają ± 4% (kolumny: 4 i 9), co mieści się w możliwych niedokładnościach odczytów z nomogramów.
Stwierdzone większe odchylenia wyników w odniesieniu do gęstości wełny wynikają prawdopodobnie z błędnego określenia typu wełny (zamiast mineralnej powinno być szklanej).
W oparciu o powyższe spostrzeżenia polecam stosowanie proponowanej modyfikacji procedury obliczeniowej, która pozwala na zwiększenie precyzji obliczeń (wiersze: 11–22) i uniknięcia konieczności odczytów z części nomogramów.
Moje wcześniejsze doświadczenia wykazują, że w opracowanych projektach ustrojów rezonansowych obliczanych wg procedury Smithsa i Kostena wykonane pomiary kontrolne potwierdzały zgodność z wynikami obliczeń.
Podsumowanie
Przeanalizowano procedurę obliczeniową ustrojów rezonansowych, zaproponowaną przez prof. Dobruckiego. Stwierdzono niedokładności w proponowanych algorytmach obliczeniowych, dotyczące określania parametrów geometrycznych ustrojów rezonansowych – dla danych wejściowych jak w opracowaniach [2, 3]. Dlatego zaproponowano modyfikację powyższej procedury, gwarantującą uzyskanie poprawnych wyników.
Podjęto próby znalezienia wzorów aproksymacyjnych do wyznaczenia zależności matematycznych dla parametrów konstrukcyjnych ustrojów rezonansowych – jak w nomogramach Smithsa i Kostena [1]. Prowadziły one jednak do bardzo złożonych algorytmów. Dlatego uznano, że prostszym rozwiązaniem jest bezpośrednie posłużenie się tymi nomogramami.
Literatura
1. J.M.A. Smiths, C.W. Kosten, „Sound absorption by slit resonators”, „Acustica” 1951, vol. 1, p. 114.
2. J. Sadowski, „Akustyka w urbanistyce, architekturze i budownictwie”, Arkady, Warszawa 1971, s. 560–566.
3. Z. Żyszkowski, „Podstawy elektroakustyki”, wyd. 3., WNT, Warszawa 1984, s. 536–541.
4. A. Dobrucki, „Projektowanie rezonansowych układów pochłaniających”, IV Sympozjom „Nowości w technice audio”, Intermedia’07, s. 13–20.
5. Kolektyw autorski, kierownictwo: W. Schirmer, „Lärmbekämpfung“, Verlag Tribüne, Berlin 1974, s. 399.