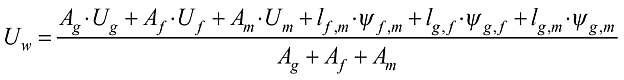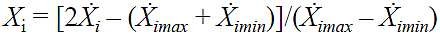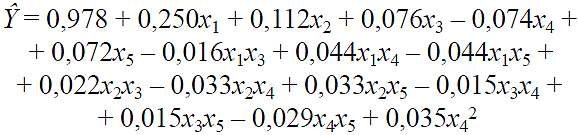Wpływ parametrów fizykalnych elementów stolarki okiennej na współczynnik przenikania ciepła okien
The influence of physical parameters of window profile components on the thermal conductivity coefficient of windows

W artykule przeanalizowano charakter i stopień wpływu najważniejszych parametrów fizykalnych charakteryzujących właściwości cieplne elementów stolarki okiennej.
Milewski
Producenci stolarki okiennej na przestrzeni ostatnich 10-15 lat wprowadzili na polski rynek okna niezwykle szczelne, o bardzo dobrej charakterystyce cieplnej. Wśród konsumentów stolarki okiennej pojawiły się możliwości szerokiego wyboru typów, rozmiarów czy konfiguracji okien z uwzględnieniem ich jakości użytkowej.
Zobacz także
BREVIS S.C. Czy nawiewniki w oknach są obowiązkowe – najważniejsze Informacje

Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu...
Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu uniknięcia negatywnych skutków zbyt dużej wilgotności, to już dyskomfort siedzenia w dusznym i nieprzewietrzonym pomieszczeniu zna każdy. Oprócz wentylacji grawitacyjnej do niedawna odpowiednią cyrkulację powietrza zapewniały nieszczelności w oknach. Jednak rozwój technologiczny i zwiększenie szczelności...
DAKO Jak wybrać drzwi do nowoczesnego domu?

Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie...
Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie aspekty trzeba zwrócić szczególną uwagę, wybierając drzwi zewnętrzne!
Czytaj całość »
RoletyAlu Sp. z o.o. Jak łatwo kupić rolety zewnętrzne przez internet?
Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość...
Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość złożenia zamówienia bezpośrednio u producenta rolet zewnętrznych pozwala wyeliminować pośredników, co skraca czas potrzeby na realizację zamówień i przekłada się na dużo niższe ceny.
Czytaj całość »Wiadomo, że okno składa się z kilku elementów ze zróżnicowanymi właściwościami cieplnymi. Ostatecznie jakość użytkowa okien, która najczęściej odbierana jest jako ich izolacyjność cieplna, zależy od dużej liczby czynników, a przede wszystkim od parametrów fizykalnych poszczególnych elementów, z których składa się całe okno oraz mostków termicznych, których nie da się uniknąć przy łączeniu różnorodnych elementów w całość.
Wśród materiałów marketingowych od producentów oraz w literaturze naukowo-technicznej figurują dane o właściwościach cieplnych elementów okien - pakietów szybowych oraz ram okiennych. Zazwyczaj producenci stolarki okiennej w standardzie najniższej ceny proponują konsumentom okna o mało korzystnym współczynniku przenikania ciepła pakietu szklącego Ug. W zależności od grubości szklenia, jakie może być zastosowane w danym oknie, producenci [1,2] wyróżniają kilka możliwości zastosowania pakietów szklących.
Przy maksymalnej grubości 36 mm zaleca się pakiet szybowy jednokomorowy o współczynniku przenikania ciepła Ug = 1,0 W/(m2·K) lub Ug = 1,1 W/(m2·K). Istnieje możliwość zastosowania pakietu trzyszybowego o współczynniku Ug = 0,7 W/(m2·K) [3].
Przy maksymalnej grubości 32 mm zaleca się pakiet szybowy o współczynniku Ug = 0,8 W/(m2·K). Dla pakietów szybowych kolejno 44 mm i 54 mm współczynniki Ug mogą wynosić 0,6 W/(m2·K) i 0,5 W/(m2·K). Producent zastrzega także możliwości zastosowania pakietów czteroszybowych w wypełnieniem z kryptonu, dla którego Ug = 0,3 W/(m2·K) [4].
Współczynnik przenikania ciepła ramy okiennej wykonanej z PVC ( Uf ), zgodnie z oceną [5] może wynosić kolejno:
- dla grubości zabudowy 70 mm i ramy ze standardowym wzmocnieniem stalowym (z układem dwóch uszczelek przylgowych:
wewnętrznej i zewnętrznej) Uf = 1,3 W/(m2·K), - dla grubości zabudowy 70 mm i ramy ze standardowym wzmocnieniem stalowym (z układem trzech uszczelek przylgowych:
wewnętrznej, środkowej i zewnętrznej) Uf = 1,2 W/(m2·K), - dla grubości zabudowy 82 mm i ramy ze standardowym wzmocnieniem stalowym (z układem dwóch uszczelek przylgowych:
wewnętrznej i zewnętrznej) Uf = 1,1 W/(m2·K), - dla grubości zabudowy 82 mm i ramy ze standardowym wzmocnieniem stalowym (z układem trzech uszczelek przylgowych:
wewnętrznej, środkowej i zewnętrznej oraz zastosowanym głębokim wrębem szyby) Uf = 1,0 W/(m2·K), - dla grubości zabudowy 90 mm i ramy ze standardowym wzmocnieniem stalowym (z układem trzech uszczelek przylgowych:
wewnętrznej, środkowej i zewnętrznej) Uf = 1,0 W/(m2·K), - dla grubości zabudowy 82 mm i ramy z termicznie dzielonym wzmocnieniem stalowym (z układem trzech uszczelek przylgowych:
wewnętrznej, środkowej i zewnętrznej oraz zastosowanym głębokim wrębem szyby i ramą skrzydła ukrytą za ramą ościeżnicy) Uf = 0,95 W/(m2·K).
ABSTRAKT |
|---|
|
W artykule przeanalizowano charakter i stopień wpływu najważniejszych parametrów fizykalnych charakteryzujących właściwości cieplne elementów stolarki okiennej (współczynnika przenikania ciepła oszklenia Ug, współczynnika przenikania ciepła ramy Uf, liniowego współczynnika przenikania ciepła mostka termicznego na styku szkło–rama ψg,f) oraz geometrycznych (powierzchni okna Aw oraz liczby skrzydeł okiennych r) na współczynnik przenikania ciepła Uw okien w budynkach mieszkalnych. Analizę wykonano na podstawie opracowanego deterministycznego modelu matematycznego opisującego tę zależność. Określono wartości optymalne badanych czynników. |
The influence of physical parameters of window profile components on the thermal conductivity coefficient of windowsThe article analyses the nature and degree of influence of the most important physical parameters characterising the thermal properties of window profile components (glazing thermal conductivity coefficient Ug, frame thermal conductivity coefficient Uf, the linear thermal conductivity coefficient of the thermal bridge at the glass-frame joint ψg,f) and the geometric properties (window surface Aw and the number of window wings r) on the thermal conductivity coefficient Uw of windows in residential buildings. The analysis was based on the developed deterministic mathematical model describing this dependence. The optimum values of the tested factors were determined. |
Według tego samego producenta [5] liniowy współczynnik mostka termicznego na styku szkło–rama ψg,f może być na poziomie 0,05 W/(m·K) dla mniej korzystnych wartości Ug i 0,035 W/(m·K) dla lepszych wartości Ug.
Niestety trudno jest doszukać się charakterystyk cieplnych dla całych okien, składających się z elementów o wyżej wymienionych parametrach. Ciężko jest również poradzić sobie przy oszacowaniu współczynnika przenikania ciepła stolarki okiennej. Ostatecznie najtrudniejszym zadaniem jest wybór, bez specjalistycznej wiedzy, konkretnych typów elementów stolarki oraz zamówienie okien.
Potrzeba oceniania i optymalizacji parametrów stolarki okiennej jest ważna szczególnie teraz, kiedy konsumenci stolarki okiennej decydują się na okna o dużych, często niestandardowych rozmiarach i kształtach, które mają pełnić funkcję przeszklonych ścian.
W związku z powyższym celem danego badania jest analiza współczynnika przenikania ciepła stolarki okiennej z PVC w budynkach mieszkalnych, w zależności od grupy czynników, obejmujących parametry fizykalne elementów stolarki okiennej i rozmiary okien, wraz z oceną stopnia i charakteru wpływu tych czynników oraz określeniem ich wartości optymalnych na podstawie deterministycznego modelu matematycznego opracowanego z danych eksperymentu obliczeniowego.
Metoda określenia współczynnika przenikania ciepła stolarki okiennej
Uznano, że do obliczania współczynnika przenikania ciepła stolarki okiennej najbardziej przydatna i oczywista jest metoda składnikowa. Według niej fragment przegrody dzieli na pola powierzchni o różnych właściwościach cieplnych, a całkowity współczynnik przenikania ciepła oblicza się za pomocą ważonych powierzchniowo wartości U elementów składowych z dodatkowymi członami korekcyjnymi, uwzględniającymi wzajemne oddziaływania cieplne między tymi elementami [6]. Współczynnik przenikania ciepła Uw pojedynczego okna należy obliczać zgodnie z równaniem:
 (1)
(1)
gdzie:
Ug, Uf, Um - współczynniki przenikania ciepła, odpowiednio:
oszklenia,
ramy
oraz słupków okiennych,
ψf,m, ψg,f, ψg,m - liniowe współczynniki przenikania ciepła spowodowane połączonymi efektami cieplnymi elementów, odpowiednio:
szklącego i ramy,
szklącego i słupka
oraz ramy i słupka okiennego,
lg,f,lg,m, lf,m - długość liniowego mostku cieplnego powstającego na styku, odpowiednio:
szkła i ramy,
szkła i słupka
oraz ramy i słupka,
Ag, Am, Af - pole powierzchni, odpowiednio:
oszklenia,
słupków okiennych
oraz ramy.
Odnosząc się do przedstawionego wzoru (1) autorzy stworzyli algorytm do wyliczania szukanego współczynnika przenikania ciepła okna Uw przy zmianie wartości wybranych czynników, który stanowił podstawę do opracowania modelu matematycznego.
Badane warianty okien oraz model matematyczny współczynnika przenikania ciepła
Rozmiary współczesnych okien w budynkach mieszkalnych ograniczone są gabarytami pomieszczeń. Wysokość okien może osiągać 2,5 m, a szerokość nawet do 4,0-5,0 m.
W oknach często występują pionowe słupki tworzące w oknie kilka skrzydeł.
Z uwzględnieniem najczęściej stosowanych rozmiarów okien oraz postawionego celu badania zostały wybrane następujące warianty stolarki okiennej:
- powierzchnia od 1,82 m2 (okno standardowe) do 5,46 m2;
- wysokość okna stała - 1,48 m;
- liczba skrzydeł - do 1 do 3.
Schematy badanych wariantów okien podano na RYS. 1–2.

RYS. 1-2. Schematy badanych wariantów stolarki okiennej: o zmiennej powierzchni (1) oraz o zmiennej liczbie skrzydeł (2); rys. archiwa autorów
Przy opracowaniu modelu matematycznego bardzo ważne jest zapewnienie jego praktycznej przydatności czy utylitarności oraz skuteczności. Takie cechy można osiągnąć opracowując krótkie modele, w których wykorzystano najważniejsze czynniki, opisujące badany proces czy właściwość oraz mające istotne znaczenie dla odbiorców informacji o badanym obiekcie.
W badaniu jako funkcję celu Y wybrano współczynnik przenikania ciepła stolarki okiennej Uw [W/(m2·K)]. Badano zależność współczynnika Uw(Y) od następujących czynników:
- współczynnika przenikania ciepła oszklenia Ug(czynnik X1),
- współczynnika przenikania ciepła ramy Uf (czynnik X2),
- liniowego współczynnika przenikania ciepła mostka, spowodowanego połączeniem elementów, ψg,f (czynnik X3),
- pola powierzchni okna Aw(czynnik X4),
- liczby skrzydeł okiennych r (czynnik X5).
Przypuszczano, że szukaną zależność Y = ƒ(X1, X2, X3, X4, X5) może opisywać wielomian drugiego stopnia.
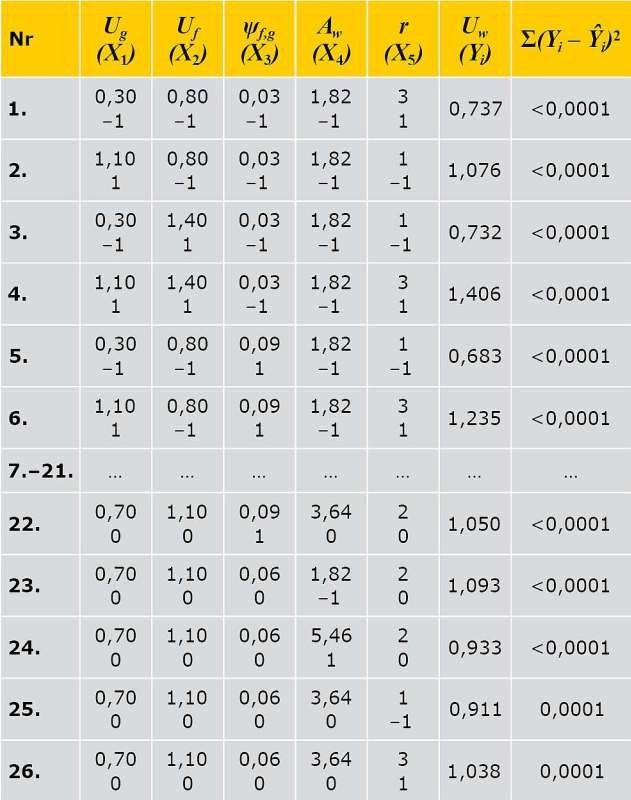
W celu uzyskania danych do opisu tej zależności przeprowadzono 5-czynnikowy eksperyment obliczeniowy według planu drugiego stopnia ( TAB. 1 ).
Zastosowano kompozycyjny symetryczny trójpoziomowy plan, zawierający 26 prób [7]. Do wyliczenia wartości Yi w 26 wierszach planu wykorzystano program Microsoft Excel.
Na RYS. 3 został przedstawiony schemat blokowy wyliczania współczynnika przenikania ciepła okien. Zaproponowany algorytm obliczeń wykorzystano do realizacji eksperymentu obliczeniowego.

RYS. 3. Schemat blokowy obliczania współczynnika przenikania ciepła Uw stolarki okiennej; rys. archiwa autorów
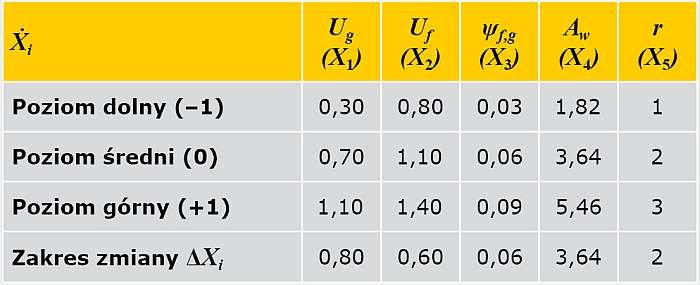
Przy wyborze zakresu zmienności czynników oraz wartości wielkości stałych, od których także zależą efekty wpływu rozpatrywanych czynników, opierano się na informacjach uzyskanych z publikacji [1,2] oraz od producentów stolarki okiennej [3,5].
Współczynnik przenikania ciepła oszklenia Ug (czynnik X1 ) na średnim poziomie przyjęto 0,7 W/(m2·K).
Na górnym poziomie wybrano wartość równą 1,1 W/(m2·K), a na dolnym - 0,3 W/(m2·K).
Współczynnik przenikania ciepła ramy Uf (czynnik X2 ) na średnim poziomie przyjęto 1,10 W/(m2·K).
Na poziomie wyższym wybrano wartość równą 1,40 W/(m2·K), a najniższa wartość przyjęta została na poziomie 0,8 W/(m2·K).
Liniowy współczynnik przenikania ciepła mostka spowodowanego połączeniem elementów szkło–rama ψg,f, (czynnik X3 ) na średnim poziomie przyjęto 0,060 W/(m·K).
Na poziomie wyższym wybrano wartość równą 0,090 W/(m·K), a najniższa wartość przyjęta została na poziomie 0,030 W/(m·K).
Pole powierzchni okna Aw (czynnik X4 ) na dolnym poziomie przyjęto równe 1,48×1,23 = 1,82 m2, tj. odpowiednie polu powierzchni okna referencyjnego [7].
Jako poziom górny przyjęto powierzchnia okna 5,46 m2, a poziom średni - 3,64 m2.
Liczbę skrzydeł okiennych r (czynnik X5 ) w budynkach mieszkalnych, z uwzględnieniem potrzeb niniejszego badania, miało sens ograniczyć do trzech. Tak więc wybrano:
- jedno skrzydło jako poziom dolny,
- dwa skrzydła jako poziom średni,
- trzy skrzydła jako poziom górny.
Pozostałe zmienne wymienione we wzorze (1) wyliczano na podstawie wartości wybranych czynników.
Wartości współczynnika przenikania ciepła słupków okiennych Um oraz liniowego współczynnika przenikania ciepła mostka spowodowanego połączeniem elementów rama–słupek okienny ψg,m zostały przyjęte na tym samym poziomie, co i wartości współczynników Uf oraz ψg,f.
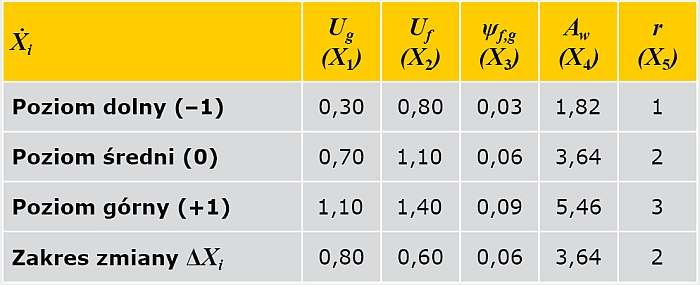
Wyżej wymienione wartości naturalne czynników Ẋ1, Ẋ2, Ẋ3, Ẋ4, Ẋ5 i odpowiadające im wartości unormowane X1, X2, X3, X4, X5 przedstawiono w TAB. 1 .
Przejście z wartości naturalnych Ẋi do unormowanych Xi wyraża się wzorem:
![]() (2)
(2)
gdzie:
Ẋi, Ẋimax, Ẋimin - odpowiednio bieżące, maksymalne i minimalne wartości naturalne i-tego czynnika.
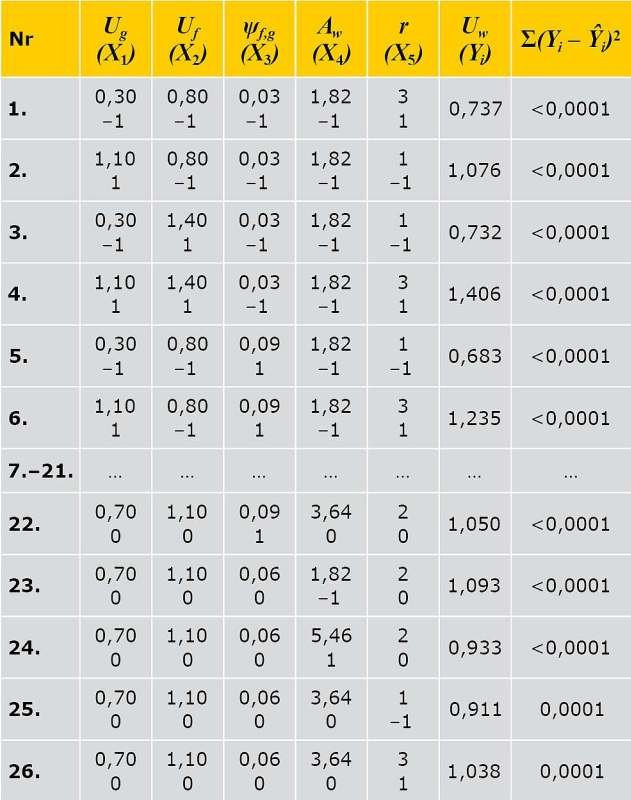
Na podstawie wyników obliczeń ( TAB. 2 ) metodą najmniejszych kwadratów [8] opracowano równanie regresji zależności
Y = ƒ(X1, X2, X3, X4, X5).
Istotność współczynników tego równania oceniono za pomocą t-kryterium. Metoda testowania współczynników szczegółowo opisana przez autorów w artykule [2]. W wyniku testu pięć współczynników okazało się nieistotnych. Po ich usunięciu przyjęto postać końcową równania z k + 1 = 16 współczynnikami:
 (3)
(3)
Adekwatność modelu została potwierdzona według metody, szczegółowo opisanej w artykule [2]. Dany model miał:
Σ ( Yi – Ŷi ) 2 = 0,0016; S2a = Σ ( Yi – Ŷi ) 2 / [ N – ( k + 1 )] = 0,0003; R2 = 0,9991
Dodatkowo jakość aproksymacji danych opracowanym równaniem oceniono według kryterium F [8].
Przy poziomie istotności α = 0,05 i liczbie stopni swobody:
ƒ1 = N – 1 = 26 – 1 = 25;
ƒ2 = N – ( k + 1) = 26 – 21 = 5
okazało się, że wartość obliczeniowa kryterium F0 = S2y/S2a = 224,1517 wielokrotnie przekracza wartość tabelaryczną F0,05;25;5 = 4,5250 [9], co potwierdza wysoką jakość uzyskanego modelu.
Analiza wpływu wybranych czynników na współczynnik przenikania ciepła okna
Za pomocą równania regresji (3) przeanalizowano stopień i charakter wpływu poszczególnych czynników na współczynnik przenikania ciepła Uw okna. Analizę przeprowadzono dla zmiennych w postaci naturalnej. Interesowały nas przede wszystkim warianty stolarki okiennej o jak najniższym współczynniku Uw.
Wykryto, że podobnie jak i we wcześniejszych badaniach autorów [1,2], na współczynnik Uw korzystny wpływ okazuje powierzchnia okna Aw(X4).
Przy zmianie Aw od 1,82 do 5,46 m2 wartość współczynnika Uw zmalała o 13,6%. Jednak wpływ Aw nie jest równomierny, o tym świadczy niewielki efekt kwadratowy tego czynnika. Przy zmianie Aw od 1,82 do 3,64 m2 współczynnik Uw zmalał o 10%, natomiast w zakresie od 3,64 do 5,46 m2 efekt wpływu tego czynnika obniża Uw tylko o 3,6%. Wiąże się to z nierównomierną zmianą udziału powierzchni szkła w stolarce okiennej przy wahaniach pola powierzchni okna, co potwierdzono dodatkowymi obliczeniami (przy Aw = 1,82 m2 udział powierzchni szklonej wynosi 0,52, przy Aw = 3,64 m2 – 0,67, a przy Aw = 5,46 m2 - 0,73).
Wraz ze wzrostem pozostałych czynników współczynnik Uw się zwiększa.
Przy zmianie wartości czynników Ug ( X1 ), Uf ( X2 ), ψf,g ( X3 ), r ( X5 ) z dolnego do górnego poziomu ( TAB. 1 ) ich niekorzystny wpływ przejawia się istotnym podwyższeniem Uw wynoszącym odpowiednio: 68,7, 25,9, 16,9 i 15,9%.
Ponieważ uzyskany model zawiera dziewięć współczynników, charakteryzujących interakcje czynników, warto przeanalizować efekty ich wspólnych oddziaływań, w których najczęściej zawarta jest nieoczekiwana i najciekawsza część informacji.
Po analizie współczynników modelu wykryto, że charakter i stopień wpływu czynników fizykalnych zależy od wartości innych czynników.
Stopień wpływu Ug (X1) wzmacnia się ze wzrostem Aw (X4) oraz słabnie ze wzrostem ψf,g (X3) i r (X5). Stopień wpływu Uf (X2) odwrotnie - wzmacnia się ze wzrostem ψf,g (X3) i r (X5) oraz słabnie ze wzrostem Aw (X4). Stopień wpływu ψf,g (X3) także słabnie ze wzrostem Aw (X4).
Jak widać, badana zależność jest dosyć skomplikowana. Związane jest to z tym, że proces przenoszenia ciepła przez stolarkę okienną ma charakter przestrzenny i zależy nie tylko od właściwości cieplnych materiału elementów okna, lecz od ich powierzchni i innych parametrów geometrycznych, określających usytuowanie przestrzenne elementów w konstrukcji okna. Część z tych parametrów podczas analizy wpływu wybranych czynników zmieniała się skokowo lub nierównomiernie.
W celu zagęszczenia analizy oraz uzyskania przydatnej i dostępnej informacji dla projektantów i konsumentów stolarki okiennej podzielono rozpatrywane okna warunkowo na grupy.
Każdą z tych grup można scharakteryzować dwoma parametrami, które zostały przyjęte w badaniu jako czynniki, a mianowicie:
- powierzchnia okna Aw (X4)
- oraz liczba skrzydeł r (X5).
W zależności od poziomu czynników okna mogą być małe ( Aw = 1,82 m2), średnich rozmiarów ( Aw = 3,64 m2) i duże ( Aw = 5,46 m2); jednoskrzydłowe ( r = 1), dwuskrzydłowe ( r = 2) i trójskrzydłowe ( r = 3).
Według tych cech okna zostały podzielone na pięć grup ( TAB. 3 ). Dalszą analizę czynników wykonano w oparciu na odpowiednią grupę okien.
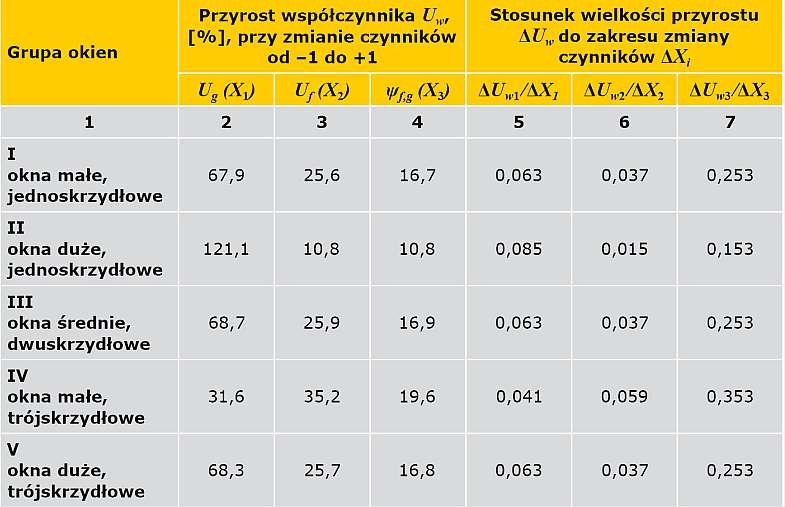
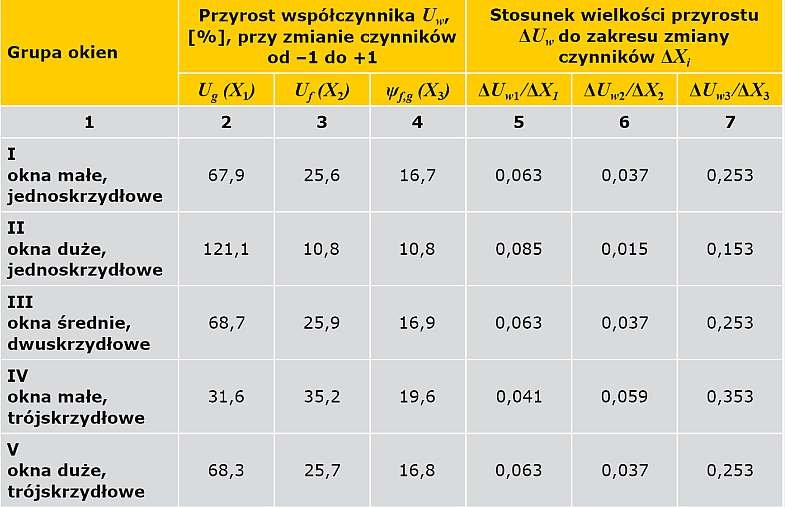
TABELA 3. Wyniki analizy wpływu czynników fizykalnych na współczynnik przenikania ciepła Uw okien z wytypowanych grup
Do oszacowania stopnia wpływu czynników fizykalnych na współczynnik przenikania ciepła Uw w kolumnach 2, 3, 4 TAB. 3 podane zostały przyrosty współczynnika Uw przy zmianie czynników z dolnego do górnego poziomu ( TAB. 1 ).
Przyrosty wyrażone w % w odniesieniu do wartości Uw uzyskanej dla dolnego poziomu odpowiedniego czynnika. Charakteryzują one moc wpływu odpowiedniego czynnika na funkcję celu Uw.
W kolumnach 5, 6, 7 podano właściwy wkład każdego z czynników w podwyższenie Uw, uzyskany poprzez dzielenie przyrostu ΔUwi na zakres zmiany czynnika ΔXi i wyrażony w [W/(m2·K)] współczynnika Uwi na każdych 0,10 W/(m2·K) odpowiedniego czynnika.
Analizując dane z TAB. 3 , można zauważyć, że dla grup okien I, III i V (gr. I - okna małe, jednoskrzydłowe; gr. III – okna średnie, dwuskrzydłowe; gr. V – okna duże, trójskrzydłowe) czynniki fizykalne mają jednakowe procentowe przyrosty Uw, jak również jednakowe właściwe wkłady.
Taka zbieżność wynika z wybranych rozmiarów okien, w których powierzchnia skrzydeł przyjęta została jako równa powierzchni okna referencyjnego (jednoskrzydłowego). Dla tych trzech grup okien stopniowe obniżenie co 0,1 W/(m2·K) czynników Ug (X1) i Uf (X2) od górnego do dolnego poziomu ( TAB. 1 ) pozwała obniżać współczynnik przenikania ciepła Uw okien odpowiednio o 0,063 i 0,037 W/(m2·K) na każdy stopień. Natomiast stopniowe obniżenie co 0,01 W/(m·K) czynnika ψf,g (X3) w zakresie od 0,09 do 0,03 W/(m·K) ( TAB. 1 ) pozwała obniżać współczynnik przenikania ciepła Uw okien o 0,025 W/(m2·K) na każdy stopień (w TAB. 3 podano właściwe wkład czynnika ψf,g (X3) w oparciu o jego stopniowe obniżenie co 0,1 W/(m·K)).
Dla okien grupy II (okna duże, jednoskrzydłowe) zauważono wzmocnienie wpływu czynnika Ug (X1), który spowodował przyrost Uw o 121,1%. Wymaga to od projektantów uważnego podejścia przy wyborze pakietów szklących dla podobnych okien. Zastosowanie w tej sytuacji stolarki okiennej w standardzie najniższej ceny nie jest dobrym rozwiązaniem, ponieważ okno o mało korzystnym współczynniku przenikania ciepła pakietu szklącego spowoduje duże straty ciepła. Warto pamiętać, że dla tej grupy okien stopniowe obniżenie co 0,1 W/(m2·K) czynnika Ug (X1) w przyjętym zakresie zmiany ( TAB. 1 ) pozwała obniżać współczynnik przenikania ciepła Uw okien o 0,085 W/(m2·K) na każdy stopień.
Odwrotnie, dla okien grupy IV (okna małe, trójskrzydłowe) wykryto wzmocnienie wkładu czynnika Uf (X2), który podwyższa Uw o 35,2%. Wzrost ten spowodowany zwiększeniem udziału powierzchni ramy okiennej w wyniku zastosowania trzech skrzydeł w oknie o małej powierzchni. Dla tej grupy okien stopniowe obniżenie co 0,1 W/(m2·K) czynnika Uf (X2) w przyjętym zakresie zmiany ( TAB. 1 ) pozwała obniżać współczynnik przenikania ciepła Uw okien o 0,059 W/(m2·K) na każdy stopień. Należy o tym pamiętać przy wyborze konstrukcji ramy okiennej.
Opisany charakter wpływu czynników odzwierciedlają wykresy na RYS. 4-5 i RYS. 6-7 .
![RYS. 4-5. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od współczynnika przenikania ciepła oszklenia Ug [W/(m2·K)] i współczynnika przenikania ciepła ramy Uf [W/(m2·K)] przy: ψf,g = 0,09 W/(m·K); Aw = 1,82 m2 (4) oraz ψf,g = 0,09 W/(m·K); Aw = 5,46 m2 (5); rys. archiwa autorów RYS. 4-5. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od współczynnika przenikania ciepła oszklenia Ug [W/(m2·K)] i współczynnika przenikania ciepła ramy Uf [W/(m2·K)] przy: ψf,g = 0,09 W/(m·K); Aw = 1,82 m2 (4) oraz ψf,g = 0,09 W/(m·K); Aw = 5,46 m2 (5); rys. archiwa autorów](https://www.izolacje.com.pl/media/cache/typical_view/data/202102/b-wplyw-parametrow-rys4-5.jpg)
RYS. 4-5. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od współczynnika przenikania ciepła oszklenia Ug [W/(m2·K)] i współczynnika przenikania ciepła ramy Uf [W/(m2·K)] przy: ψf,g = 0,09 W/(m·K); Aw = 1,82 m2 (4) oraz ψf,g = 0,09 W/(m·K); Aw = 5,46 m2 (5); rys. archiwa autorów
![RYS. 6-7. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od współczynnika przenikania ciepła mostka ψg,f [W/(m·K)] przy: Ug = 1,1 W/(m2·K); Aw = 1,82 m2 (6) oraz Ug = 1,1 W/(m2·K); Aw = 5,46 m2; rys. archiwa autorów RYS. 6-7. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od współczynnika przenikania ciepła mostka ψg,f [W/(m·K)] przy: Ug = 1,1 W/(m2·K); Aw = 1,82 m2 (6) oraz Ug = 1,1 W/(m2·K); Aw = 5,46 m2; rys. archiwa autorów](https://www.izolacje.com.pl/media/cache/typical_view/data/202102/b-wplyw-parametrow-rys6-7.jpg)
RYS. 6-7. Zależność współczynnika przenikania ciepła stolarki okiennej Uw [W/(m2·K)] od współczynnika przenikania ciepła mostka ψg,f [W/(m·K)] przy: Ug = 1,1 W/(m2·K); Aw = 1,82 m2 (6) oraz Ug = 1,1 W/(m2·K); Aw = 5,46 m2; rys. archiwa autorów
W wyniku optymalizacji równania regresji (3) wykryto, że uzyskana funkcja osiąga minimalną (najlepszą) wartość Uw,min = 0,459 W/(m2·K) przy następujących wartościach czynników: Ug = 0,30 W/(m2·K); Uf = 0,80 W/(m2·K); ψg,f = 0,03 W/(m·K); Aw = 5,46 m2; r = 1.
Przy zapewnieniu minimalnej wartości Uw,min wkłady omawianych elementów w proces przenoszenia ciepła przez okno wynosiły:
- powierzchni szklącej - 51%,
- ramy - 38%,
- mostków liniowych - 11%.
Maksymalną (najgorszą) wartość Uw,max = 1,626 W/(m2·K) obserwuje się przy Ug = 1,10 W/(m2·K), Uf = 1,40 W/(m2·K), ψg,f = 0,09 W/(m·K), Aw = 1,82 m2, r = 3. Wtedy wkłady poszczególnych elementów w proces przenoszenia ciepła wynosiły:
- powierzchni szklącej - 24%,
- ramy - 56%,
- mostków liniowych - 20%.
Uzyskane dane z przeprowadzonego badania niosą przydatną informację o wpływie parametrów fizykalnych na współczynnik przenikania ciepła okien i mogą być wykorzystane przy podjęciu decyzji podczas wyboru elementów stolarki okiennej.
Opracowany model matematyczny dla zbiorów dowolnych wartości badanych czynników (w przyjętych zakresach zmienności) po ich unormowaniu według wzoru (2) pozwala obliczyć współczynnik przenikania ciepła stolarki okiennej.
Wnioski
- Zaproponowany deterministyczny model matematyczny pozwolił dokładnie określić charakter i stopień wpływu parametrów fizykalnych w wybranym zakresie ich zmienności na współczynnik przenikania ciepła Uw okien przy zmianie ich pola powierzchni i liczby skrzydeł.
- Wykryto, że stopień i charakter wpływu czynników fizykalnych na współczynnik Uw stolarki okiennej zmienia się przy wahaniach wartości pozostałych czynników, ponieważ ich wpływ jest mocno obciążony interakcją czynników geometrycznych.
- Dla wybranych grup okien z określonymi parametrami geometrycznymi zaproponowano wskaźnik w postaci właściwego wkładu czynników w podwyższenie Uw, pozwalający oszacować efekty zastosowania różnych typów elementów stolarki okiennej.
- Ustalono, że optymalne wartości zbadanych czynników to są: Ug = 0,30 W/(m2·K); Uf = 0,80 W/(m2·K); ψg,m = 0,03 W/(m·K); Aw = 5,46 m2; r = 1. Pozwalają one osiągnąć minimalną wartość współczynnika Uw,min = 0,459 W/(m2·K).
Literatura
- W. Jezierski, J. Borowska, "Analiza parametrów cieplnych współczesnej stolarki okiennej", "IZOLACJE" 4/2017.
- W. Jezierski, J. Borowska, "Parametry cieplne wieloskrzydłowej stolarki okiennej w budynkach mieszkalnych", "IZOLACJE" 6/2017.
- Strona internetowa: www.drutex.pl.
- PN-EN 673, "Szkło w budownictwie, Określanie współczynnika przenikania ciepła U. Metoda obliczeniowa".
- Strona internetowa: www.veka.pl
- PN-EN ISO 12631:2013-03, "Cieplne właściwości użytkowe ścian osłonowych. Obliczanie współczynnika przenikania ciepła".
- Z. Polański, "Planowanie doświadczeń w technice", PWN, Warszawa 1984.
- K. Hartmann, E. Lezki, W. Schär, "Statistische Versuchsplanung und auswertung in der Stoffwirtschaft", VEB, Leipzig 1977.
- W. Krysicki, J. Bartos, W. Dyczka, K. Królikowska, M. Wasilewski, "Rachunek prawdopodobieństwa i statystyka matematyczna w zadaniach, część II Statystyka matematyczna", PWN, Warszawa 2003.





![RYS. 4–5. Zależność współczynnika przenikania ciepła stolarki okiennej <em><strong>U<sub>w</sub></strong></em> [W/(m<sup>2</sup>·K)] od współczynnika przenikania ciepła oszklenia <em><strong>U<sub>g</sub></strong></em> [W/(m<sup>2</sup>·K)] i współczynni.](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/wplyw-parametrow-rys4-5.jpg)
![RYS. 6–7. Zależność współczynnika przenikania ciepła stolarki okiennej <em><strong>U<sub>w</sub></strong></em> [W/(m<sup>2</sup>·K)] od współczynnika przenikania ciepła mostka<em><strong> ψg,f</sub></strong></em> [W/(m·K)]
przy: <em><strong>U<sub>g</sub.](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/wplyw-parametrow-rys6-7.jpg)