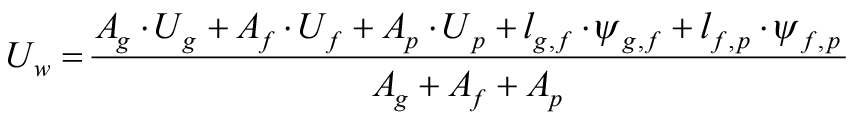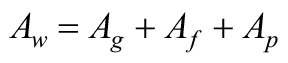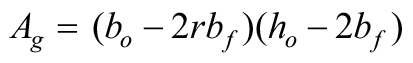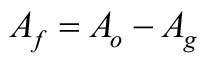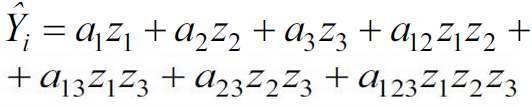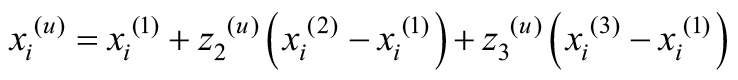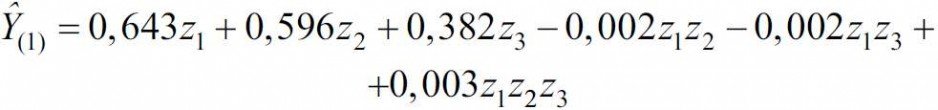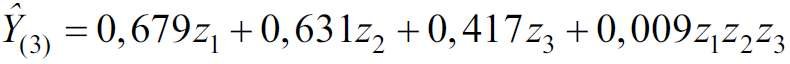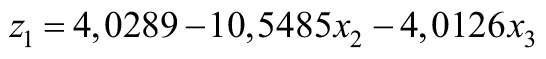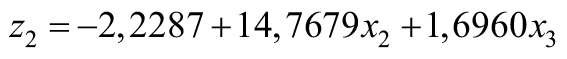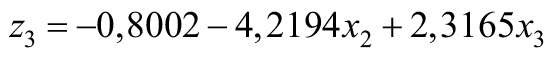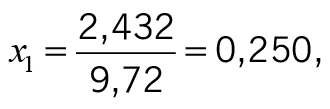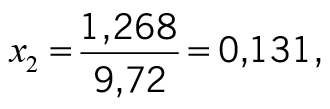Analiza przenikania ciepła w ścianie osłonowej z oknem wieloskrzydłowym
Analysis of heat transfer in the curtain wall with a multi-sash window

Ściana osłonowa każdego pomieszczenia w budynkach mieszkalnych najczęściej jest fragmentem składającym się z odcinka ściany pełnej i okna.
Milewski.
Zgodnie z obowiązującymi przepisami w Polsce [1], maksymalny dopuszczalny współczynnik przenikania ciepła dla ścian osłonowych w budynkach nowo wznoszonych wynosi Umax = 0,23 W/(m2·K), zaś dla okien Umax = 1,10 W/(m2·K). Należy jednakże zauważyć, że konstrukcja ściany zewnętrznej zazwyczaj jest podobna w każdym budynku przeznaczonym na pobyt stały ludzi - jej członem zasadniczym jest ściana pełna, w której osadzone jest okno składające się z ramy i części szklonej.
Architekci wkładają wiele wysiłku w to, by odpowiednio zaprojektować budynki mieszkalne tak, aby każda przegroda spełniała stawiane im wymagania. Niejednokrotnie jest to o tyle kłopotliwe, że nawet jeśli są znane parametry cieplne materiałów konstrukcyjnych ściany, to dane dotyczące stolarki okiennej zazwyczaj nie są podawane bezpośrednio do wiedzy konsumentów.
W związku z powyższym autorzy uważają, że należy oszacować stopień wpływu pól powierzchni poszczególnych elementów składowych oraz przeanalizować wpływ skrzydeł stolarki okiennej na całkowity współczynnik przenikania ciepła fragmentów ściany osłonowych z oknami. Taka informacja będzie wzmacniać intuicję projektantów i pozwoli szybciej znajdować optymalne rozwiązania przegród budowlanych. Tylko wówczas można prawidłowo wyliczyć współczynnik przenikania ciepła kompleksowej ściany zewnętrznej.
Celem niniejszego badania jest analiza wpływu udziałów powierzchni elementów składowych (ściany pełnej, ramy okiennej i powierzchni szklonej) oraz liczby skrzydeł w oknie wieloskrzydłowym na współczynnik przenikania ciepła ściany osłonowej z oknem wykonanym z PVC w budynku mieszkalnym, z opracowaniem deterministycznych modeli matematycznych zależności oraz oszacowaniem stopnia wpływu badanych czynników.
Opis obiektu badania
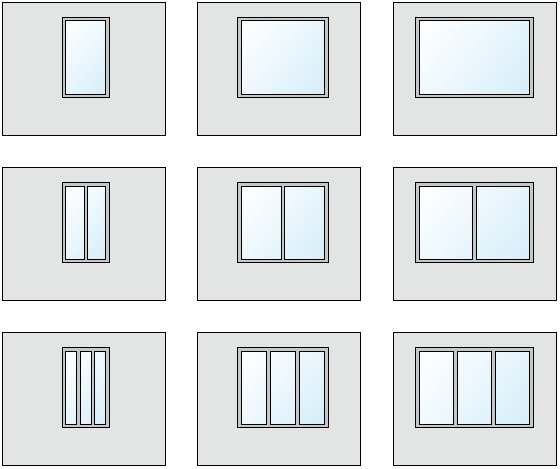
Ściana osłonowa każdego pomieszczenia w budynkach mieszkalnych najczęściej jest fragmentem składającym się z odcinka ściany pełnej i okna. Z uwzględnieniem nowych technologii montażu okien z PVC, jako obiekt badania dla dalszej analizy przyjęto fragment ściany z trzema elementami: ścianą pełną, ramą okienną i powierzchnią szkloną. Schematy takiego fragmentu pokazano na RYS. 1.
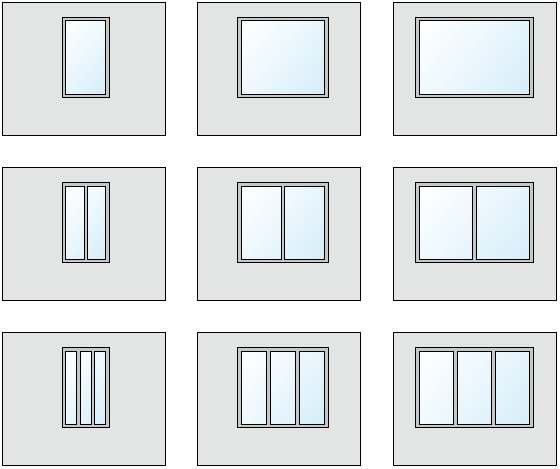
RYS. 1. Schematy badanego fragmentu ściany osłonowej z oknem o różnej konfiguracji; rys.: archiwum autorów
Z uwzględnieniem rozwiązań przestrzennych pomieszczeń mieszkalnych przyjęte zostały następujące rozmiary fragmentu ściany: 2,70×3,60 m (wysokość×szerokość) = 9,72 m2.
W ramach tej wartości w badaniu zmieniały się różne kombinacje pól powierzchni okien, od rozmiaru 1,2×1,48 m = 1,776 m2 do 3,20×1,48 m = 4,736 m2.
Wysokość okna w analizowanym przypadku należało przyjąć jako wartość stałą, równą wysokości okna referencyjnego, która wynosi 1,48 m [2].
Abstrakt |
|---|
|
W artykule przeanalizowano wpływ udziałów powierzchni elementów składowych (odcinków ściany pełnej, ramy okiennej i powierzchni szklonej) oraz liczby skrzydeł w oknie wieloskrzydłowym na współczynnik przenikania ciepła ściany osłonowej z oknem wykonanym z PVC w budynku mieszkalnym. Przy realizacji eksperymentu obliczeniowego zastosowano lokalne planowanie sympleksowe w warunkach ograniczenia zakresu zmienności wybranych czynników. Analiza wykonana została na podstawie opracowanych deterministycznych modeli matematycznych opisujących tę zależność.
Analysis of heat transfer in the curtain wall with a multi-sash window
The article analyses the impact of surface shares of component parts (sections of a full wall, window frame and glazed surface) and the number of sashes in a multi-sash window on the heat transfer coefficient of a curtain wall with a window made of PVC in a residential building. While implementing the computational experiment, local simplex planning was used in the conditions of limiting the range of variability of selected factors. The analysis was made on the basis of developed deterministic mathematical models describing this relationship. |
Metoda obliczania współczynnika przenikania ciepła
Współczynnik przenikania ciepła fragmentu ściany osłonowej z oknem wieloskrzydłowym obliczano według metody składnikowej [3].
Według tej metody współczynnik przenikania ciepła Uw układu "ściana osłonowa + rama okienna + oszklenie" należy obliczać za pomocą wzoru:
 (1)
(1)
gdzie:
Ug, Uƒ, Up - współczynniki przenikania ciepła, odpowiednio: oszklenia, ramy oraz ściany pełnej,
ψg,ƒ, ψƒ,p - liniowe współczynniki przenikania ciepła spowodowane połączonymi efektami cieplnymi elementów, odpowiednio: szklącego i ramy oraz ramy i ściany pełnej,
lg,ƒ, lƒ,p - długość liniowego mostku cieplnego powstającego na styku, odpowiednio: szkła i ramy oraz ramy i ściany pełnej,
Ag, Aƒ, Ap, Aw - pole powierzchni, odpowiednio: oszklenia, ramy, ściany pełnej oraz fragmentu ściany osłonowej.
Nawet przy trzech elementach składowych wzór ten daje ponad 10 czynników do przeanalizowania. Każdy dodatkowy element składowy, w zależności od lokalizacji, zwiększa liczbę czynników o 4-6 parametrów.
Jednak najtrudniejszym zadaniem do przeprowadzenia analizy jest warunek, którym są powiązane trzy pierwsze zmienne:
![]() (2)
(2)
Odnosząc się do przedstawionego wzoru (1), autorzy stworzyli algorytm do wyliczania szukanego współczynnika przenikania ciepła okna Uw przy zmianie wartości wybranych czynników (RYS. 2).

RYS. 2. Schemat blokowy obliczania współczynnika przenikania ciepła Uw fragmentu ściany osłonowej, gdzie ho, bo, Ao to odpowiednio: wysokość, szerokość i powierzchnia okna; r - liczba skrzydeł w oknie; C - udział powierzchni szklonej do powierzchni okna; bƒ - szerokość elementów ramy; rys.: archiwum autorów
W tym algorytmie przewiduje się wprowadzenie wartości pól powierzchni oszklenia Ag i ramy Af.
Przy znanych rozmiarach okna (bo - szerokość, ho - wysokość, Ao - powierzchnia), liczbie skrzydeł r i szerokości elementów ramy bƒ wartości Ag, Aƒ można obliczyć w następujący sposób:
![]() (3)
(3)
![]() (4)
(4)
Algorytm posłużył jako podstawa do opracowania autorskiego programu komputerowego w Microsoft Excel.
Model matematyczny do określenia współczynnika przenikania ciepła
Analiza przedstawionych czynników pozwoliła wykryć, że oprócz zmiennych Ag, Aƒ, Ap oraz r, lg,ƒ, lƒ,p pozostałe zmienne są sterowalne, mierzalne, wzajemnie niezależne, niesprzeczne i odpowiadają podstawowym wymaganiom modelowania matematycznego [4]. Zmienne lg,ƒ i lƒ,p są niejednoznaczne oraz zależne od Ag i Aƒ.
W celu zapewnienia jednoznaczności lg,ƒ i lƒ,p wysokość okna przyjęto jako wartość stałą.
Zgodnie z przyjętym celem badania, współczynnik przenikania ciepła Uw fragmentu ściany (funkcja celu Y) postanowiono zbadać w zależności od czynników geometrycznych - udziałów powierzchni szklonej (czynnik z1), powierzchni ramy (czynnik z2) i powierzchni ściany pełnej (czynnik z3) oraz liczby skrzydeł w oknie r.
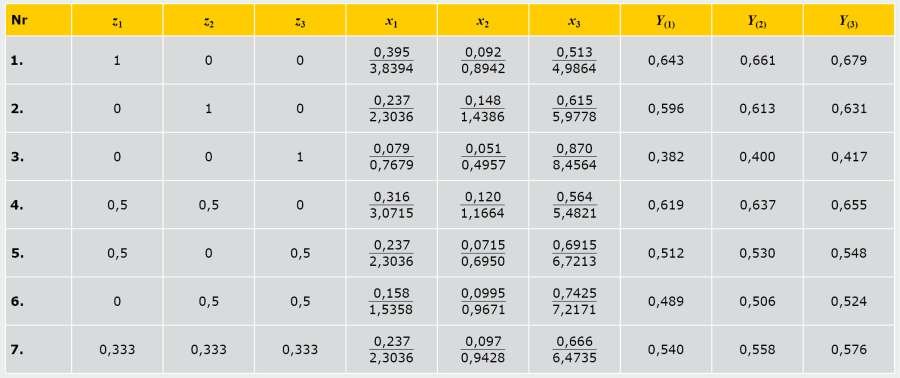
Ponieważ czynniki geometryczne z1, z2, z3 są związane warunkiem (2), to do zbadania ich wpływu zastosowano planowanie sympleksowe dla trzech zmiennych w układzie "skład-własność", zawierającego N = 7 prób (TABELA) [5].
Plan sympleksowy przewiduje określony układ realizacji obliczeń przy spełnieniu warunku z1+ z2+ z3 = 1 i opracowanie modelu w postaci niepełnego wielomianu trzeciego stopnia dla trzech zmiennych:
 (5)
(5)
Sensownym rozwiązaniem była analiza przy liczbie skrzydeł w oknie od 1 do 3. Odpowiada to realnym rozwiązaniom stolarki okiennej w budynkach mieszkalnych oraz pozwala wykryć charakter i stopień wpływu tego czynnika. Jednak zmiana liczby skrzydeł okna powoduje skokowe zmiany udziałów powierzchni szkła, ramy i ściany.
Uwzględnienie liczby skrzydeł w oknie jako czwartego czynnika w modelu było praktycznie niemożliwe przy zastosowaniu planowania sympleksowego.
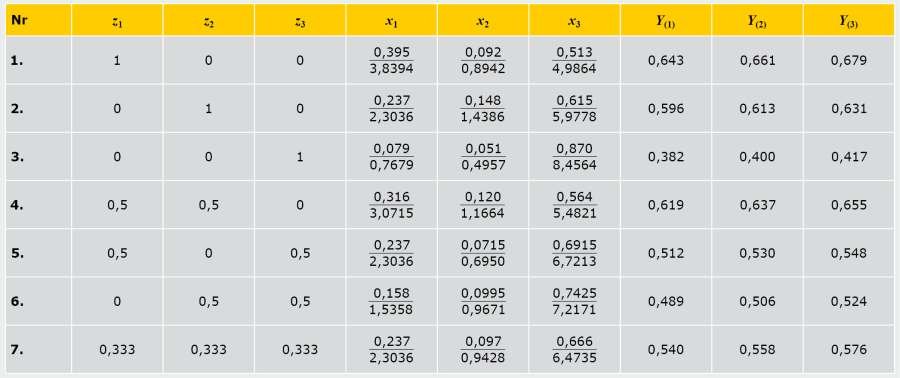
TABELA. Plan sympleksowy dla trzech zmiennych na N = 7 prób, gdzie z1, z2, z3 - kodowane czynniki; χ1, χ2, χ3, – naturalne czynniki geometryczne (w liczniku - udziały, w mianowniku - powierzchnie, m2); Y(1), Y(2), Y(3) - wyniki obliczeń współczynnika przenikania ciepła ściany osłonowej z oknem dla r = (1), (2), (3)
Dążąc do osiągnięcia celu badania, podjęto decyzję o opracowaniu modelu w postaci Y(i) = ƒ(z1, z2, z3) dla każdej z trzech konfiguracji okna: jedno-, dwu- i trójskrzydłowego (odpowiednio Y(1), Y(2), Y(3)).
Pozostałe zmienne niezależne przyjęto na stałym poziomie.
Wartości czynników fizykalnych Ug, Uf,Up przyjęto na poziomie odpowiadającym współczesnym wymaganiom:
Ug = 0,70 W/(m2·K);
Uƒ = 1,10 W/(m2·K);
Up = 0,23 W/(m2·K).
Wartości liniowych współczynników przenikania ciepła na granicy szkło–rama oraz rama–ściana przyjęto w obu przypadkach na poziomie 0,080 W/(m2·K) [6].
Nie było potrzeby wykonywania badania w całym zakresie zmiany wybranych czynników, ponieważ np. przy z1 = 1 analizowany fragment składałby się wyłącznie z oszklenia.
Praktyczne znaczenie miały jedynie te zakresy zmienności czynników, które odpowiadają realnym układem fragmentu ściany z oknem. W związku z tym w badaniu zastosowano lokalne planowanie sympleksowe w warunkach ograniczenia zakresu zmienności wszystkich czynników [7].
Na podstawie wstępnej analizy parametrów wybranego fragmentu ściany osłonowej z oknem został wybrany podobszar obejmujący preferowane udziały elementów składowych, który określały współrzędne Ai (χ1; χ2; χ3) wierzchołków trójkąta
A1 (0,395; 0,092; 0,513);
A2 (0,237; 0,148; 0,615);
A3 (0,079; 0,051; 0,870).
Wyżej wymieniony podobszar został transformowany do pełnego planu sympleksowego poprzez wprowadzenie pseudoskładników z1, z2, z3, które w każdym u-tym układzie planu są związane z czynnikami rzeczywistymi χ1, χ2, χ3 zależnością [7]:
![]() (6)
(6)
Poziomy zmienności czynników z1, z2, z3 oraz odpowiadające im rzeczywiste czynniki χ1, χ2, χ3 przedstawiono w TABELI.
Po przeprowadzeniu obliczeń współczynnika przenikania ciepła fragmentu ściany Yi wg planu oraz korzystając z metody podanej w [5], opracowano zależności Y(i) = ƒ(z1, z2, z3):
- dla okna jednoskrzydłowego:
 (7)
(7)
- dla okna dwuskrzydłowego:
 (8)
(8)
- dla okna trójskrzydłowego:
![]() (9)
(9)
Po określeniu współczynników wykonano testowanie adekwatności modeli (7), (8) i (9) wg kryterium Fiszera [8] i uznano ich przydatność do dalszej analizy.
Dla praktycznego zastosowania uzyskanych modeli otrzymano również formuły związku pomiędzy współrzędnymi naturalnymi ƒi a współrzędnymi zi:
![]() (10)
(10)
![]() (11)
(11)
![]() (12)
(12)
Testowanie uzyskanych modeli matematycznych oraz procedura opracowania formuł związku zostały szczegółowo opisane przez autorów w pracy [9].
Analiza wyników badania
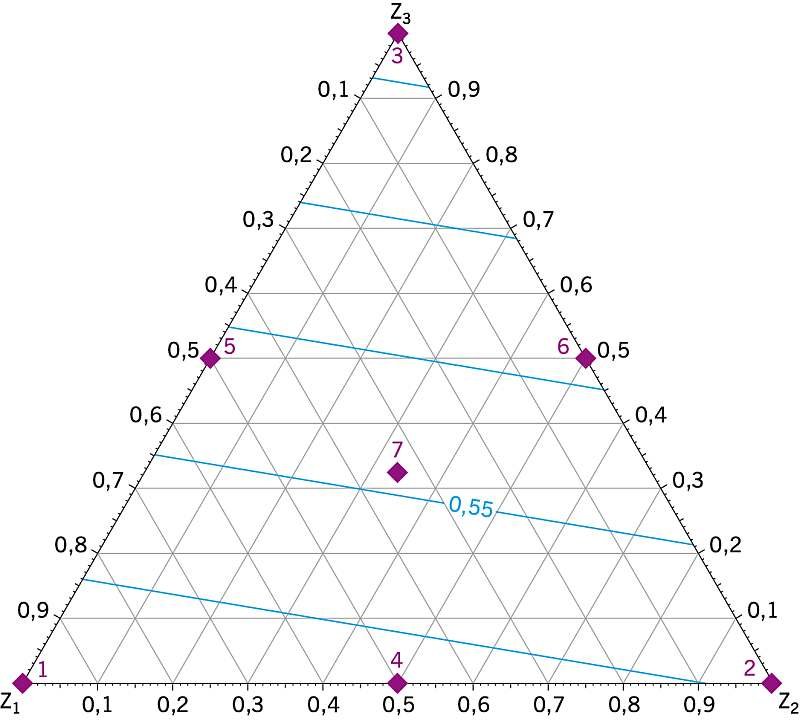
Na podstawie modeli (7) i (9) opracowano wykresy w postaci izolinii badanych zależności Yi = ƒ(z1, z2, z3) od rozpatrywanych czynników we współrzędnych pseudoskładników z1, z2, z3 dla fragmentów ściany z oknem (RYS. 3, RYS. 4). Te modele pozwoliły powiększyć badany podobszar do pełnych trójkątów sympleksowych, znacznie ułatwiając interpretację wyników. Natomiast merytoryczną interpretację wykonano w oparciu o tabelę przy zastosowaniu naturalnych współrzędnych χ1, χ2, χ3.
Jak widać z RYS. 3, najwyższą wartość [0,643 W/(m2 · K)] współczynnika przenikania ciepła Y(1) fragmentu ściany z oknem jednoskrzydłowym uzyskano w wierzchołku Z1 przy χ1 = 0,395; χ2 = 0,092; χ3 = 0,513 (TABELA), natomiast najniższą [0,418 W/(m2·K)] – przy χ1 = 0,132; χ2 = 0,051; χ3 = 0,817.
W sensie praktycznym oznacza to, że w badanym fragmencie ściany zamiana okna jednoskrzydłowego z powierzchnią Ao3= 1,48×1,20 = 1,776 m2 na okno jednoskrzydłowe z powierzchnią Ao2 = 1,48×3,20 = 4,736 m2 spowoduje wzrost współczynnika przenikania ciepła Y(1) fragmentu ściany z oknem o 53,8%.
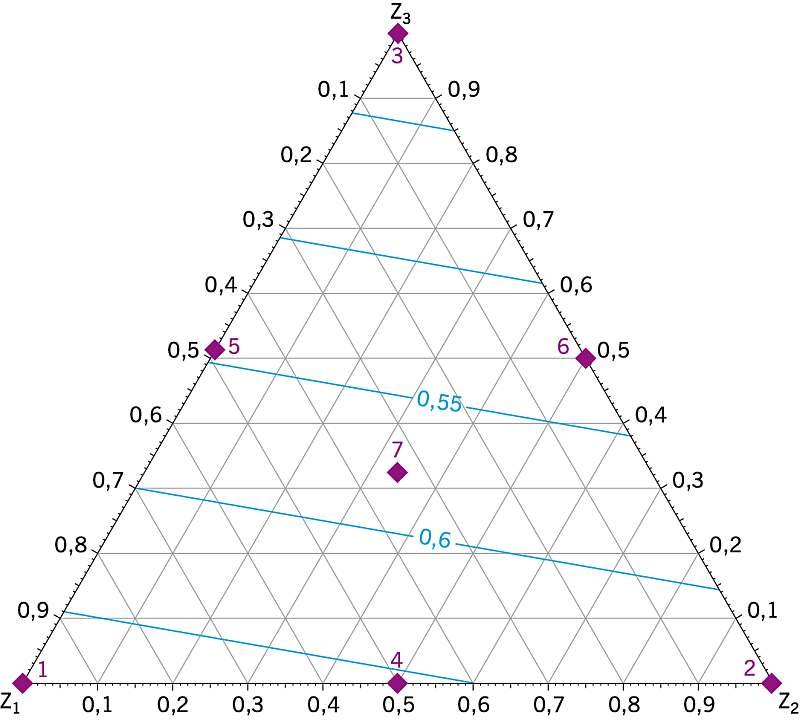
Dla fragmentu ściany z oknem trójskrzydłowym najwyższa wartość 0,70 W/(m2·K) współczynnika przenikania ciepła Y(3) występuje w punkcie ze współrzędnymi dla dużego okna (RYS. 4):
χ1 = 0,342;
χ2 = 0,145;
χ3 = 0,513.
Natomiast dla okna małego (przy χ1= 0,079; χ2 = 0,104; χ3 = 0,817) obserwuje się wartość Y(3) wynoszącą 0,475 W/(m2·K).
Powyższe oznacza, że zamiana okna trójskrzydłowego z powierzchnią Ao3 = 1,48×1,20 = 1,776 m2 na okno trójskrzydłowe z powierzchnią Ao2 = 1,48×3,20 = 4,736 m2 spowoduje wzrost współczynnika przenikania ciepła Y(3) badanego fragmentu ściany z oknem o 47,4%.
Spadek stopnia wzrostu współczynnika przenikania ciepła fragmentu ściany z oknem trójskrzydłowym o 6,3% od wzrostu dla okna jednoskrzydłowego związany jest z ponownym podziałem udziałów pól powierzchni oszklenia i ramy przy niezmiennych rozmiarach okien.
 |
 |
| RYS. 3. Zależność współczynnika przenikania ciepła Y1 fragmentu ściany z oknem jednoskrzydłowym od udziałów: z1 - powierzchni oszklenia, z2 - powierzchni ramy, z3 - powierzchni ściany; rys.: archiwum autorów | RYS. 4. Zależność współczynnika przenikania ciepła Y3 fragmentu ściany z oknem trójskrzydłowym od udziałów: z1 - powierzchni oszklenia, z2 - powierzchni ramy, z3 - powierzchni ściany; rys.: archiwum autorów |
Wykryto, że w wybranym zakresie zmienności (od 1,776 do 4,736 m2) wzrost powierzchni okna na każdy 1 m2 daje przyrost współczynnika przenikania ciepła badanego fragmentu ściany:
- z oknem jednoskrzydłowym o 18,2%,
- dwuskrzydłowym o 16,9%,
- trójskrzydłowym o 16,0%.
Ustalono również, że zastosowanie okna trójskrzydłowego w badanym fragmencie ściany zwiększa jego współczynnik przenikania ciepła w porównaniu z jednoskrzydłowym:
- o 13,6% - dla okna małych rozmiarów (1,776 m2),
- o 10,6% - dla okna średnich rozmiarów (3,256 m2),
- o 8,9% - dla okna dużych rozmiarów (4,736 m2).
Minimalną wartość współczynnika przenikania ciepła badanego fragmentu ściany z oknem, wynoszącą 0,418 W/(m2·K), osiągnięto przy zastosowaniu okna jednoskrzydłowego z najmniejszą powierzchnią Ao3 = 1,776 m2.
Na przykładzie zostanie pokazana możliwość zastosowania opracowanych modeli do praktycznych obliczeń.
Zakładamy, że chcemy obliczyć współczynnik przenikania ciepła fragmentu ściany z oknem trójskrzydłowym (r = 3) o powierzchni wynoszącej:1,48(ho)×2,50(bo) = 3,70(Ao) · m2.
Pozostałe dane przyjęto tak jak w badaniu.
Rozwiązanie składa się z czterech kroków:
- Krok 1: Obliczamy Ag wg wzoru (3) oraz Aƒ wg wzoru (4):
Ag = (2,50 – 2 · 3 · 0,1)(1,48 – 2 · 0,1) = 2,432 m2,
Aƒ = 3,70 – 2,432 = 1,268 m2.
- Krok 2: Obliczamy udziały powierzchni elementów składowych:
oszklenia:

ramy:

ściany:
χ3 = 1 – 0,250 – 0,131 = 0,619.
- Krok 3: Obliczamy wartości kodowane czynników zi wg formuł związku (10, 11, 12):
z1 = 4,0289 – 10,5485 · 0,131 – 4,0126 · 0,619 = 0,163,
z2 = –2,2287 + 14,7679 · 0,131 + 1,6960 · 0,619 = 0,756,
z3 = –0,8002 – 4,2194 · 0,131 + 2,3165 · 0,619 = 0,081.
- Krok 4: Obliczamy wartość współczynnika przenikania ciepła fragmentu ściany Ŷ(3) z oknem trójskrzydłowym wg modelu (9):
Ŷ(3) = 0,679 · 0,163 + 0,631 · 0,756 + 0,417 · 0,081 + 0,009 · 0,163 + 0,756 · 0,081 = 0,622 W/(m2 · K).
Obliczenie wartości Uw dla tych samych warunków zapomocą programu komputerowego dało identyczny wynik: 0,622 W/(m2 · K). Taka zbieżność jest potwierdzeniem głównej zalety modeli deterministycznych.
Wnioski
- Za pomocą opracowanych modeli matematycznych oszacowano efekty wpływu udziałów pól powierzchni oszklenia, ramy i ściany na współczynnik przenikania ciepła fragmentu ściany osłonowej z oknem wieloskrzydłowym z PVC w budynku mieszkalnym.
- W badanym zakresie zmienności (od 1,776 do 4,736 m2) wzrost powierzchni okna na każdy 1 m2 daje przyrost współczynnika przenikania ciepła analizowanego fragmentu ściany z oknem jednoskrzydłowym - o 18,2%, dwuskrzydłowym - o 16,9%, trójskrzydłowym - o 16,0%.
- Zastosowanie okna trójskrzydłowego zwiększa współczynnik przenikania ciepła ściany w porównaniu z jednoskrzydłowym o 13,6% - dla okien małych rozmiarów (1,776 m2), o 10,6% - dla okien średnich rozmiarów (3,256 m2), o 8,9% - dla okien dużych rozmiarów (4,736 m2).
- Minimalną wartość współczynnika przenikania ciepła badanego fragmentu ściany z oknem, wynoszącą 0,418 W/(m2·K), osiągnięto przy zastosowaniu okna jednoskrzydłowego o powierzchni Ao3 = 1,776 m2.
Literatura
- Rozporządzenie Ministra Infrastruktury w sprawie warunków technicznych, jakim powinny odpowiadać budynki i ich usytuowanie z dnia 17 lipca 2015 r. (DzU 2015 poz. 1422).
- PN-EN 14351-1+A2:2016-10, "Okna i drzwi - Część 1: Okna i drzwi zewnętrzne bez właściwości dotyczących odporności ogniowej i/lub dymoszczelności".
- PN-EN ISO 13789:2008, "Właściwości cieplne budynków. Współczynnik strat ciepła przez przenikanie i wentylacje. Metoda obliczania".
- J. Gutenbaum, "Modelowanie matematyczne systemów", Wyd. EXIT, Warszawa 2003.
- V.Z. Brodskiy i in., "Tablicy planow eksperimenta dla faktornych i polinomial’nych modelej", "Metalurgija", Moskwa 1982.
- PN-EN ISO 14683:2008, "Mostki cieplne w budynkach. Liniowy współczynnik przenikania ciepła. Metody uproszczone i wartości orientacyjne".
- I.G. Zedginidze, "Matematiczeskoje planirowanie eksperimenta dla issledowanija i optimizaciji swojstw smesej", "Mecniereba", Tbilisi 1986.
- K. Hartmann, E. Lezki, W. Schär, "Statistische Versuchsplanung und - auswertung in der Stoffwirtschaft", VEB, Leipzig 1977.
- W. Jezierski, J. Borowska, "Model matematyczny współczynnika przenikania ciepła ściany osłonowej z oknem z uwzględnieniem powierzchni elementów składowych", "IZOLACJE" 1/2018, s. 50-54.