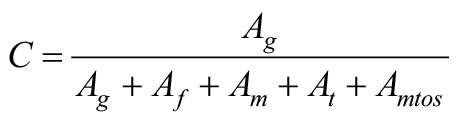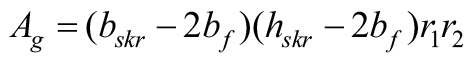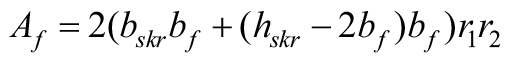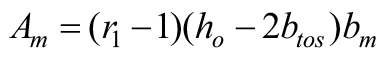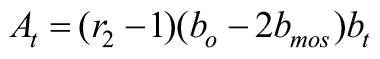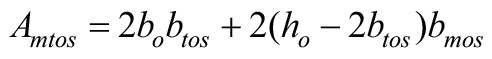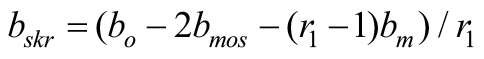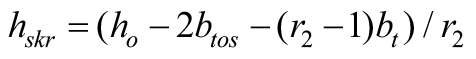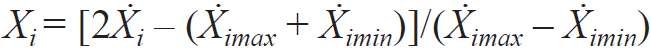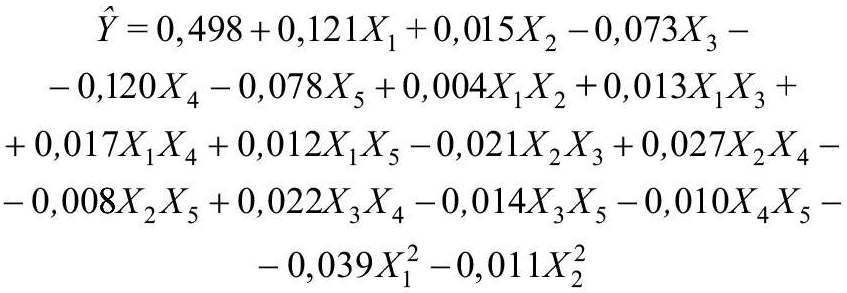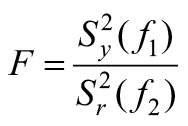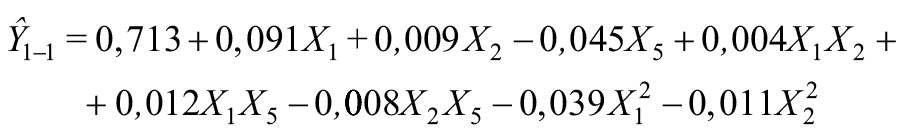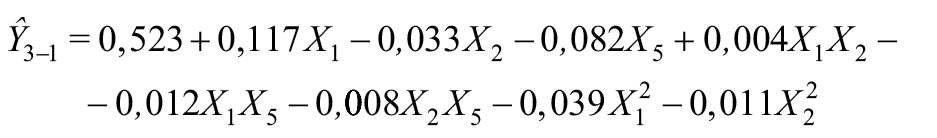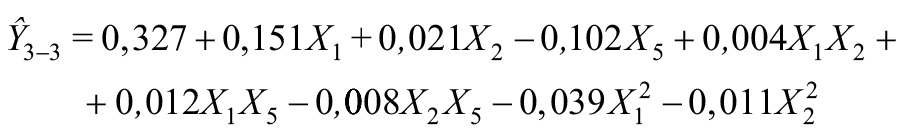Analiza warunków dopływu energii słonecznej przez wieloskrzydłowe okna o zmiennej konfiguracji
Analysis of the conditions of solar energy supply through variable configuration multi-sash windows

Poznaj warunki dopływu energii słonecznej przez okna wieloskrzydłowe do wnętrza budynku
Archiwum redakcji
Zapotrzebowanie na ciepło do ogrzewania pomieszczeń w budynku zależy od różnicy między stratami a zyskami ciepła. Straty ciepła przez przenikanie w budynku są proporcjonalne do powierzchni elementów przegród budowlanych i ich współczynników przenikania ciepła. Natomiast wielkość zysków ciepła od promieniowania słonecznego przenikającego przez powierzchnię oszkloną zależy od natężenia promieniowania słonecznego występującego w obszarze budynku, przepuszczalności promieniowania słonecznego dla przezroczystej części okien, powierzchni oszklenia, orientacji okien według stron horyzontu, nachylenia okien do poziomu, zacienienia [1].
Zobacz także
BREVIS S.C. Czy nawiewniki w oknach są obowiązkowe – najważniejsze Informacje

Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu...
Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu uniknięcia negatywnych skutków zbyt dużej wilgotności, to już dyskomfort siedzenia w dusznym i nieprzewietrzonym pomieszczeniu zna każdy. Oprócz wentylacji grawitacyjnej do niedawna odpowiednią cyrkulację powietrza zapewniały nieszczelności w oknach. Jednak rozwój technologiczny i zwiększenie szczelności...
DAKO Jak wybrać drzwi do nowoczesnego domu?

Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie...
Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie aspekty trzeba zwrócić szczególną uwagę, wybierając drzwi zewnętrzne!
Czytaj całość »
RoletyAlu Sp. z o.o. Jak łatwo kupić rolety zewnętrzne przez internet?
Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość...
Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość złożenia zamówienia bezpośrednio u producenta rolet zewnętrznych pozwala wyeliminować pośredników, co skraca czas potrzeby na realizację zamówień i przekłada się na dużo niższe ceny.
Czytaj całość »
ABSTRAKT |
|---|
|
W artykule wykonano analizę parametru charakteryzującego warunki dopływu energii słonecznej do wnętrza budynku, a mianowicie udziału pola powierzchni szklonej do całkowitego pola powierzchni okna C w zależności od pięciu czynników: pola powierzchni okna Ao, proporcji okna θ, liczby skrzydeł okiennych r1 w kierunku poziomym, liczby skrzydeł okiennych r2 w kierunku pionowym oraz szerokości elementów ramy bƒ. |
Analysis of the conditions of solar energy supply through variable configuration multi-sash windowsThe article analyses the parameter characterising the solar energy supply to the interior of the building, namely – the share of the glass surface area in the total window area C, depending on five factors: the window area Ao, the window proportion θ, the horizontal window sash count r1, the vertical window sash count r2 and the width of the frame elements bƒ. |
Przepuszczalność promieniowania słonecznego określa, jaka część promieniowania słonecznego przenika do pomieszczenia. Charakteryzuje się ona bezwymiarowym współczynnikiem g. Ten współczynnik zależy od liczby szyb oraz zastosowanych powłok selektywnych i oblicza się go według metody podanej w PN-EN 410:2001 [2]. Jego wartość według PN-EN ISO 13790-2005 [3] mieści się w zakresie od 0,77 dla oszklenia pojedynczą szybą bez powłoki do 0,45 dla oszklenia potrójnego z dwiema powłokami.
Natomiast powierzchnię oszklenia przy obliczeniu zysków wg rozporządzenia Ministra Infrastruktury i Rozwoju [1] proponuje się określać metodą uproszczoną - mnożenie powierzchni okna przez udział pola powierzchni szklonej do całkowitego pola powierzchni okna C, przy czym dla wskaźnika C przyjmuje się wartość średnią równą 0,7.
Nawet wstępne obliczenia wskaźnika C przeprowadzone przez autorów pokazały, że zależy on od współoddziałujących między sobą powierzchni oszklenia i ramy, a także związanej z nimi szerokości elementów ramy oraz liczby skrzydeł w oknie. W zależności od powierzchni okna, jego konfiguracji i liczby skrzydeł wartość wskaźnika C mieści się w zakresie od 0,30 do 0,90. Z punktu widzenia autorów zastosowanie wartości średniej wskaźnika C = 0,7 w obliczeniach zysków jest podejściem niedokładnym i powodującym potencjalne błędy.
W związku z ukazanymi powyżej zależnościami, celem danego badania jest analiza parametru charakteryzującego warunki dopływu energii słonecznej do wnętrza, a mianowicie udziału pola powierzchni szklonej do całkowitego pola powierzchni okna C, w zależności od pięciu czynników:
- pola powierzchni okna Ao,
- proporcji okna θ,
- liczby skrzydeł okiennych r1w kierunku poziomym,
- liczby skrzydeł okiennych r2 w kierunku pionowym,
- szerokości elementów ramy skrzydłowej bf.
Badanie przeprowadzono dla wieloskrzydłowych okien o zmiennej konfiguracji, wykonanych z PVC.
Opis badanego obiektu
Rozmiary współczesnych okien w budynkach często są ograniczone gabarytami pomieszczeń. Wysokość okien lub przegród przezroczystych może osiągać nawet ponad 2,5 m. Szerokość okien waha się w dużym zakresie, nawet od 0,60 m do 3-4 m. W oknach stosuje się kilka skrzydeł.
W badaniu przyjęto okna z PVC składające się z następujących elementów:
- górnego i dolnego ramiaka ościeżnicy,
- dwóch stojaków ościeżnicy,
- jednakowych rozmiarów skrzydeł, które tworzą górny, dolny i dwa boczne ramiaki oraz oszklenie,
- ślemii i stojaków do mocowania skrzydeł.
Nazwy elementów podano według normy PN-EN 12519:2007 "Okna i drzwi. Terminologia" [4].
Z uwzględnieniem najczęściej stosowanych rozmiarów okien oraz założonym celem badania zostały wybrane następujące warianty stolarki okiennej:
- powierzchnia - od 1,20 m2 do 3,60 m2,
- proporcje okna, czylistosunek wysokości okna do jego szerokości - od 0,5 do 1,
- liczba skrzydeł w kierunku poziomym i pionowym jednakowa - od 1 do 3.
Szerokość elementów ramy (ramiaków skrzydłowych) przyjęto zmienne od 0,07 m do 0,11 m. Wybrane czynniki w najwyższym stopniu i bezpośrednio charakteryzują konfigurację okien. Schematy badanych wariantów okien podano na RYS. 1.
Metoda obliczania udziału pola powierzchni szklonej do całkowitego pola powierzchni okna
Przy założeniu, że pole powierzchni okna tworzą oszklenie, rama skrzydłowa, stojaki i ślemia oraz ramiaki i stojaki ościeżnicy, udział pola powierzchni szklonej do całkowitego pola powierzchni okna C, charakteryzujący warunki dopływu energii słonecznej i oświetlenia dziennego do wewnątrz, można obliczyć ze wzoru:
 (1)
(1)
gdzie:
Ag, Aƒ, Am, At, Amtos - pole powierzchni, odpowiednio: oszklenia, ramy skrzydłowej, stojaków, ślemii, stojaków i ramiaków ościeżnicy.
Wartości tych pól powierzchni mogą być określone ze wzorów:

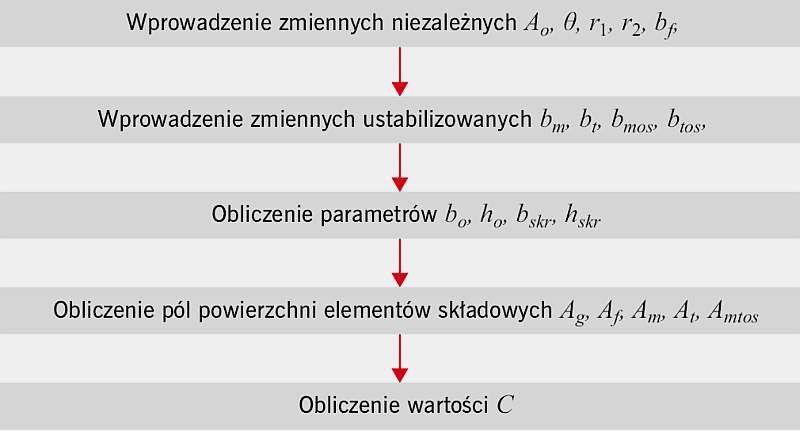
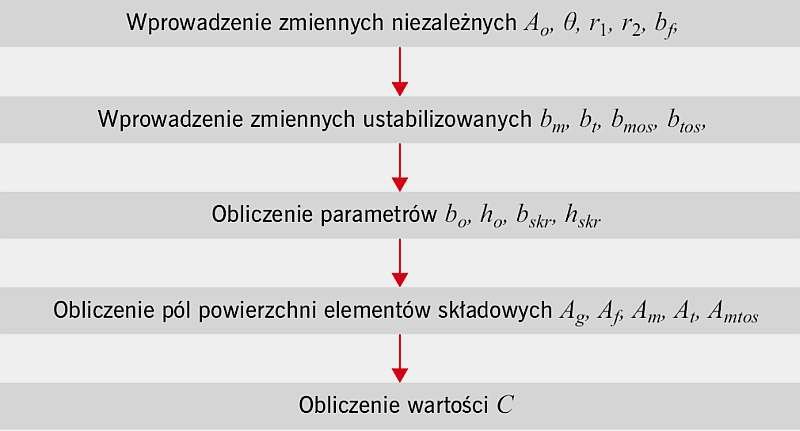
Rys. 2. Schemat blokowy obliczania udziału pola powierzchni szklonej do całkowitego pola powierzchni okna C; rys.: archiwa autorów
gdzie:
bo, bskr, bƒ, bm, bt, bmos, btos - szerokość, odpowiednio: okna, pojedynczego skrzydła, elementów ramy skrzydłowej, stojaków, ślemii, stojaków i ramiaków ościeżnicy,
ho, hskr - wysokość, odpowiednio: okna, pojedynczego skrzydła,
r1, r2 - liczba skrzydeł w kierunku poziomym i pionowym.
Odnosząc się do przedstawionych wzorów (1-8), autorzy stworzyli algorytm do wyliczania szukanego wskaźnika C przy zmianie wartości wybranych czynników ( RYS. 2 ). Algorytm posłużył jako podstawa do opracowania autorskiego programu w Microsoft Excel.
Model matematyczny udziału pola powierzchni szklonej do całkowitego pola powierzchni okna
Przy modelowaniu matematycznym właściwości systemów technicznych bardzo ważne jest, by zapewnić praktyczną przydatność modelu, a także jego utylitarność oraz skuteczność. Takie cechy można osiągnąć, opracowując krótkie modele, w których wykorzystuje się najważniejsze czynniki opisujące badane właściwości oraz zapewniające uzyskanie informacji interesującej odbiorców.
Czynniki w modelu należy przyjmować jako sterowalne, jednoznaczne, niesprzeczne i wzajemnie niezależne [5].
Zgodnie z przyjętym celem badania, udział pola powierzchni szklonej do całkowitego pola powierzchni okna C przyjęto jako funkcję celu Y, którą postanowiono zbadać w zależności od pięciu czynników geometrycznych:
- pola powierzchni okna Ao(czynnik χ1),
- proporcji okna θ wyrażonej stosunkiem wysokości okna do jego szerokości (czynnik χ2),
- liczby skrzydeł okiennych r1 w kierunku poziomym (czynnik χ3),
- liczby skrzydeł okiennych r2 w kierunku pionowym (czynnik χ4),
- szerokości elementów ramy skrzydłowej bf (czynnik χ5).
Przypuszczano, że szukaną zależność Y = ƒ(X1, X2, X3, X4, X5) może opisywać wielomian drugiego stopnia. Do uzyskania danych dla opisu tej zależności przeprowadzono 5-czynnikowy eksperyment obliczeniowy według planu drugiego stopnia ( TAB. A i TAB. B ). Zastosowano kompozycyjny symetryczny trójpoziomowy plan, zawierający 26 prób [6]. Do wyliczenia wartości Yi w 26 wierszach planu wykorzystano oprogramowanie Microsoft Excel.
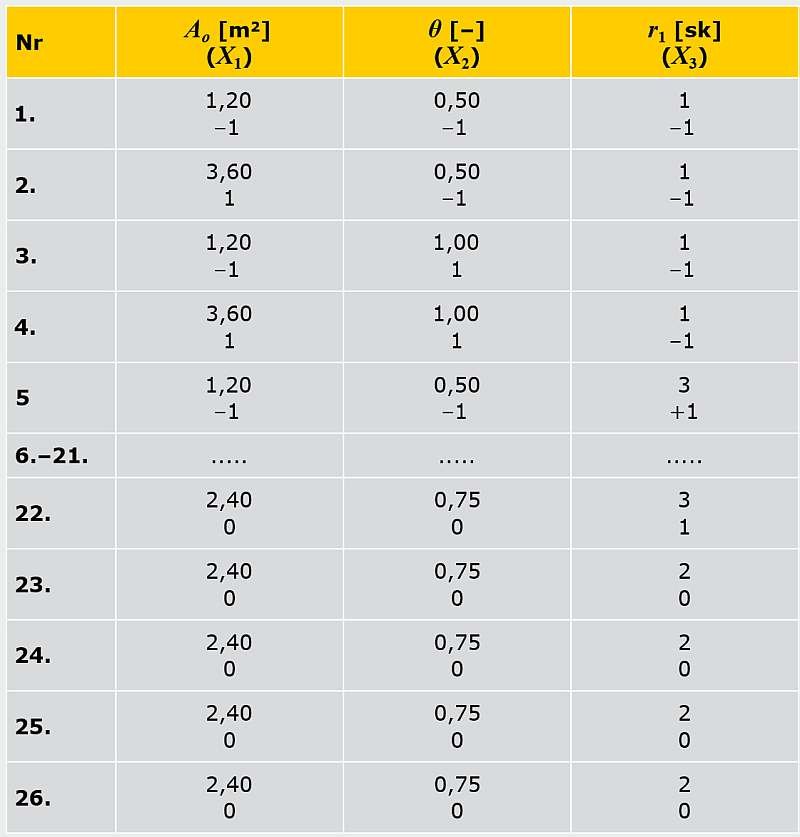
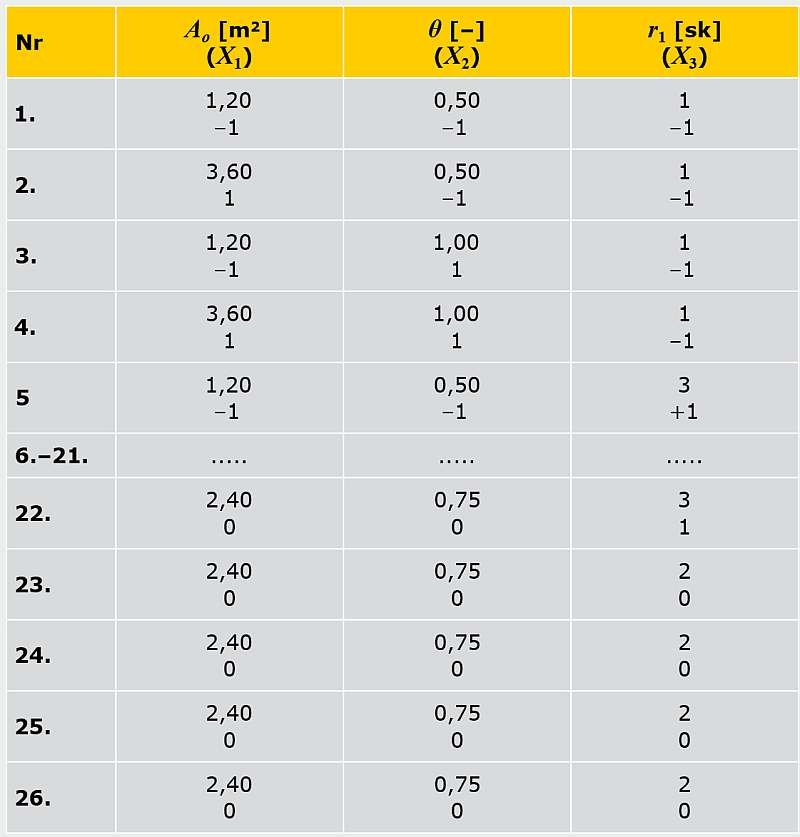
TABELA A. Plan eksperymentu obliczeniowego dla pięciu zmiennych na N = 26 prób, gdzie: Ao, θ, r1, r2, bƒ - naturalne czynniki geometryczne; X1, X2, X3, X4, X5 - kodowane czynniki; Yi - wyniki obliczeń wartości C
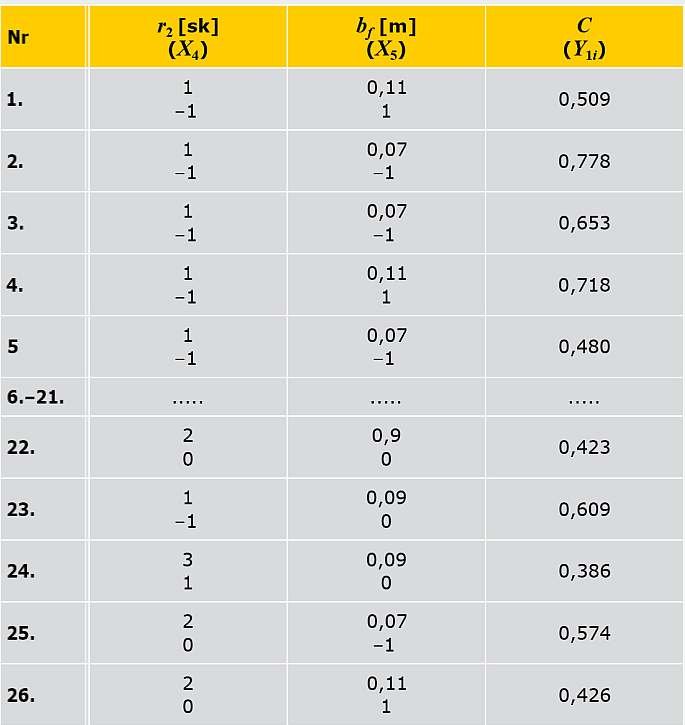
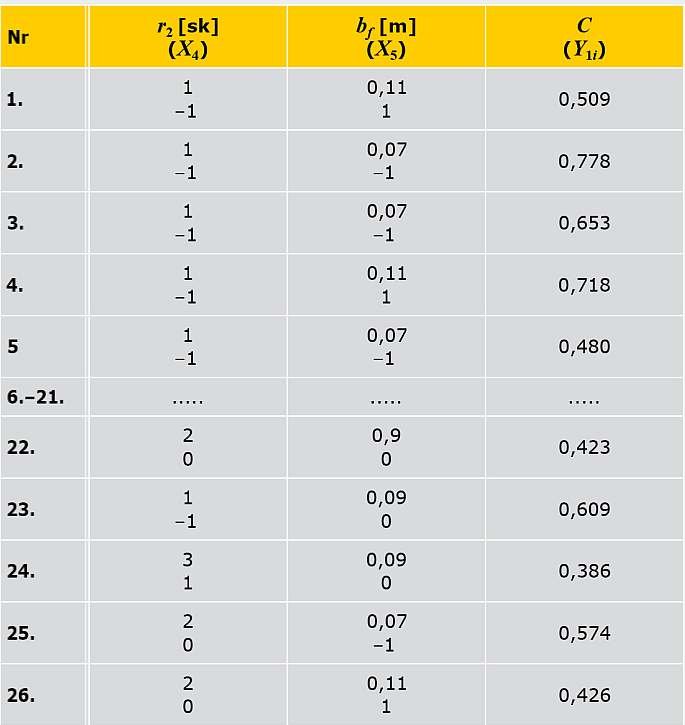
TABELA B (dokończenie TAB. A). Plan eksperymentu obliczeniowego dla pięciu zmiennych na N = 26 prób, gdzie: Ao, θ, r1, r2, bƒ -naturalne czynniki geometryczne; X1, X2, X3, X4, X5 - kodowane czynniki; Yi - wyniki obliczeń wartości C
Przy wyborze zakresu zmienności czynnika X1, czyli pola powierzchni okna (Ao), zostały przyjęte trzy poziomy: 1,20 (–1); 2,40 (0); 3,60 (+1) m2. Tak ukształtowany zakres zmienności wielkości otworów okiennych jest wystarczającym dla wykrycia efektów wpływu tego czynnika.
Czynnik X2, czyli proporcje okna (θ), przyjęto na poziomach: 0,50 (–1); 0,75 (0); 1,00 (+1). Zakres ten zapewnia możliwość analizy okien od kształtu prostokątnego 1:2 do kwadratowego 1:1.
Czynniki X3 - liczba skrzydeł w kierunku poziomym (r1) i X4 - liczba skrzydeł w kierunku pionowym (r2) przyjęto na jednakowych poziomach: 1 (–1); 2 (0); 3 (+1).
Ostatni czynnik X5 czyli szerokość elementów ramy skrzydłowej (bƒ), również przyjęto na trzech poziomach: 0,07 (–1); 0,09 (0); 0,11 (+1) m.
Wyżej wymienione wartości naturalne czynników Ẋ1, Ẋ2, Ẋ3, Ẋ4, Ẋ5 i odpowiadające im wartości unormowane X1, X2, X3, X4, X5 przedstawiono w TAB. A i TAB. B.
Przejście z wartości naturalnych Ẋi do unormowanych Xi wyraża się wzorem [6]:
![]() (9)
(9)
gdzie:
Ẋi, Ẋimax, Ẋimin - odpowiednio bieżące, maksymalne i minimalne wartości naturalne i-tego czynnika.
Pozostałe zmienne wejściowe przyjęto na stałym poziomie. Szerokość stojaków i ślemii wybrano jednakową i równą 0,02 m, a szerokość stojaków i ramiaków ościeżnicy - 0,035 m.
Na podstawie wyników obliczeń (tabela) przy zastosowaniu metody najmniejszych kwadratów [7] opracowano model w postaci równania regresji zależności Y = ƒ (X1, X2, X3, X4, X5). Po ocenie istotności współczynników uzyskanego modelu za pomocą t-kryterium [7] wykryto, że trzy czynniki są nieistotne. Po wyeliminowaniu tych czynników postać ostateczna modelu jest następująca:
 (10)
(10)
Przy testowaniu adekwatności modelu uwzględniono, że modele deterministyczne charakteryzują się wzajemnie jednoznaczną zgodnością pomiędzy oddziaływaniem zewnętrznym a reakcją na to oddziaływanie. Z tego powodu w każdym punkcie planu wykonano tylko jedno doświadczenie. Do testowania zastosowano kryterium Fiszera, które pokazuje, o ile razy zmniejsza się rozsiew odnośnie równania regresji w porównaniu z rozsiewem odnośnie średniego [7]:
 (11)
(11)
gdzie:
S2y - wariancja średniej, S2r - wariancja resztkowa,
ƒ1, ƒ2 - liczby stopni swobody, ƒ1 = (N – 1) = 26 – 1 = 25, ƒ2 = (N – Nb) = 26 – 18 = 8,
N - liczba wykonanych obliczeń,
Nb - liczba współczynników w równaniu regresji.
Równanie regresji opisuje wyniki obliczeń adekwatnie, jeżeli wartość F jest większa od wartości tabelarycznej Ft przy poziomie istotności p oraz stopniach swobody ƒ1 i ƒ2.
Jak wynika z obliczeń F = 0,0314/0,00003 = 1040,8427, wartość tabelaryczna Ft = F 0,05; 25; 8 = 2,340 [7].
Tak więc wartość F wielokrotnie przekracza Ft, co oznacza, że model jest adekwatny i przydatny do dalszej analizy. Jego wysoką jakość potwierdza również współczynnik determinacji R2 = 0,9997.
Analiza badanej zależności na podstawie modelu matematycznego
Wpływ badanych czynników na udział pola powierzchni szklonej do całkowitego pola powierzchni okna C przeanalizowano na modelu matematycznym (10). W celu zapewnienia lepszej klarowności omówienie wyników zostanie dokonane na zmiennych naturalnych.
Interesujące były przede wszystkim parametry okien zapewniające najwyższy poziom wielkości wskaźnika C. Pod tym względem czynniki w analizie występują jako korzystne, jeżeli C wraz z ich wzrostem rośnie, lub niekorzystne, jeżeli wraz z ich wzrostem C maleje.
Analizując opracowany model, wykryto, że w centrum Gp przestrzeni czynnikowej, które charakteryzuje się współrzędnymi Ao = 2,40 m2, θ = 0,75 [–], r1 = 2, r2 = 2, bƒ = 0,09 m, wielkość C wynosi 0,498 [–].
Wykorzystując punkt Gp jako punkt odniesienia, oszacowano wpływ poszczególnych czynników.
Okazało się, że najmocniejszy i korzystny wpływ na wielkość C wykazuje pole powierzchni okna Ao(X1).
Przy zmianie wartości Ao od 1,20 do 3,60 m2 (pozostałe czynniki podczas analizy charakteryzują się współrzędnymi dla punktu Gp) następuje zwiększanie się wskaźnika C od 0,338 do 0,580 [–], tj. wzrost o 71,6%.
Słaby korzystny efekt wykazuje czynnik θ(X2) - przy jego zmianie od 0,5 do 1,0 [–] ma miejsce wzrost wskaźnika C od 0,472 do 0,502, tj. o 6,4%.
Pozostałe czynniki wykazują niekorzystny wpływ - wraz z ich wzrostem wskaźnik C maleje o 25,6% dla r1(X3), o 38,8% dla r2(X4), o 27,1% dla bƒ (X5).
Z punktu widzenia praktycznego sensowne było przeanalizowanie wpływu badanych czynników dla lekko odbieranych i dobrze znanych wariantów okien: 1-skrzydłowego, 3-skrzydłowego z trzema skrzydłami w kierunku poziomym oraz 9-skrzydłowego z trzema skrzydłami w dwóch kierunkach (RYS. 3).
Zmieniając w modelu (10) czynniki X3 i X4 na odpowiednie wartości, uzyskano modele pomocnicze do analizy:
- przy X3 = –1 i X4 = –1:
 (12)
(12)
- przy X3 = +1 i X4 = –1:
 (13)
(13)
- przy X3 = +1 i X4 = +1:
 (14)
(14)
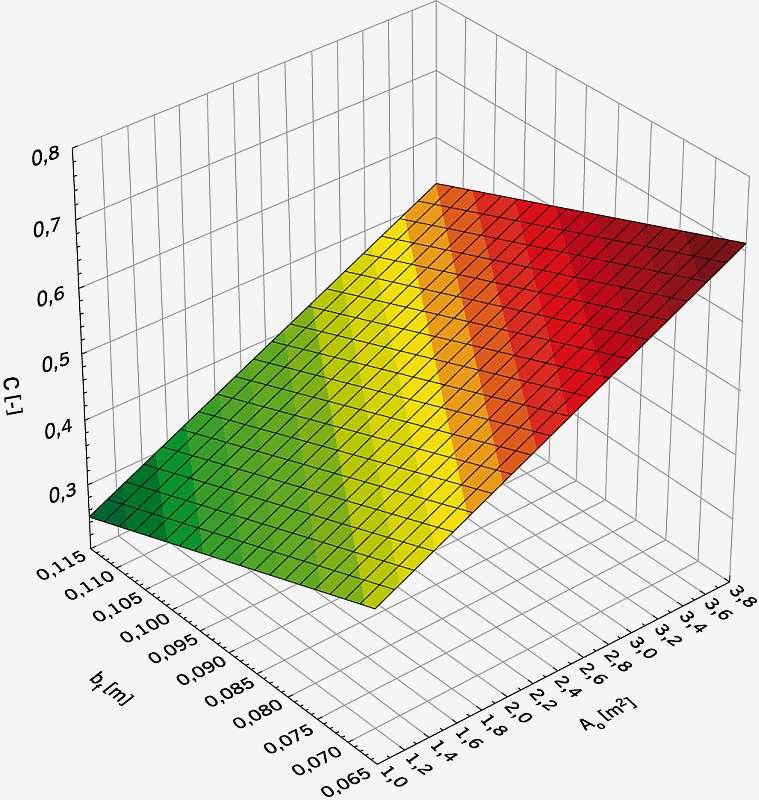
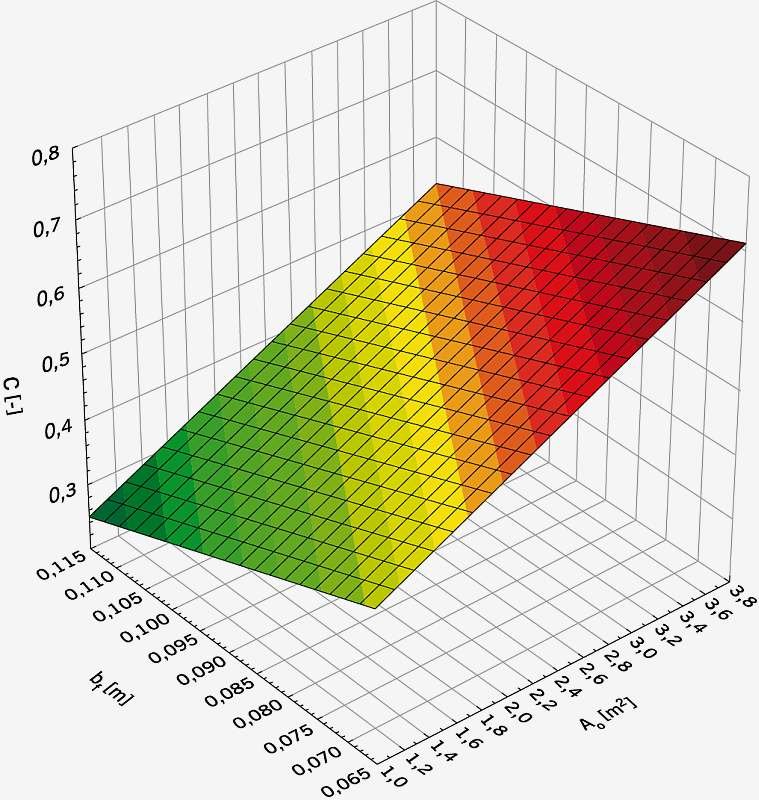
Rys. 3. Zależność udziału pola powierzchni szklonej do całkowitego pola powierzchni okna C od powierzchni Ao, m2, i szerokości elementów ramy bƒ, m, okna przy proporcji okna θ = 0,75 oraz liczbie skrzydeł r1 = 2, r2 = 2; rys.: archiwa autorów
Porównując modele (12), (13), (14), można zauważyć, że zwiększenie liczby skrzydeł z 1 do 3 w oknie mającym parametry Ao = 2,40 m2, θ = 0,75 [–], bƒ = 0,09 m, powoduje zmniejszenie wskaźnika C od 0,713 do 0,523 [–], tj. o 26,7%, a zastosowanie w tym samym oknie 9 skrzydeł obniża wskaźnik C od 0,713 do 0,327 [–], tj. spadek o 54,1% w porównaniu z oknem 1-skrzydłowym.
Wraz ze wzrostem liczby skrzydeł wzmacnia się wpływ czynnika Ao(X1). Można stwierdzić, że na każdy dodany 1 m2 powierzchni okna wskaźnik C wzrasta o 0,075 [–] dla okna 1-skrzydłowego, o 0,098 [–] dla okna 3-skrzydłowego, 0,125 [–] dla okna 9-skrzydłowego. Fakt ten wynika z tego, że wraz ze wzrostem pola powierzchni okna rośnie z wyprzedzeniem jego pole powierzchni szklonej.
Ze wzrostem liczby skrzydeł wyraźnie wzmacnia się niekorzystny wpływ czynnika bf (X5). Można stwierdzić, że na każdy dodany 1 cm szerokości ramy okiennej wskaźnik C spada o 0,023 [–] dla okna 1-skrzydłowego, o 0,041 [–] dla okna 3-skrzydłowego, 0,051 [–] dla okna 9-skrzydłowego.
Jak widać z analizy, zalecana w rozporządzeniu [1] wartość wskaźnika C na poziomie 0,7 [–] jest (i to wątpliwie) przydatna do scharakteryzowania warunków dopływu energii słonecznej tylko dla okien 1-skrzydłowych. Jest ona bardzo przybliżona, ponieważ nie uwzględnia wpływu pola powierzchni okien i szerokości elementów ramy.
Za pomocą numerycznej symulacji modelu (12) ustalono, że efekty wahań tych czynników w przyjętym w badaniu zakresie zmienności rozmywają wartość wskaźnika C od 0,512 do 0,808 [–], co istotnie różni się od zalecanej w rozporządzeniu [1] wartości.
Tak więc nawet dla okien 1-skrzydłowych przy obliczeniach zysków ciepła należy sprecyzować udział pola powierzchni szklonej do całkowitego pola powierzchni okna C.
Autorzy proponują stosować w tym celu opracowane w niniejszym artykule wzory (2), (7), (8) do oszacowania wartości wskaźnika C dla okien wieloskrzydłowych zmiennej konfiguracji.
Na przykładzie zostanie pokazana możliwość zastosowania tych wzorów do praktycznych obliczeń. Zakładamy, że chcemy obliczyć udział pola powierzchni szklonej do całkowitego pola powierzchni okna C o następujących parametrach:
- pole powierzchni okna wynosi Ao = 1,48×2,40 = 3,552 m2,
- liczba skrzydeł w kierunku poziomym r1 = 3,
- liczba skrzydeł w kierunku pionowym r2 = 2,
- szerokość elementów ramy okiennej bƒ = 0,08 m.
Szerokość stojaków i ślemii wybrano jednakową i równą bm = bt = 0,02 m, a szerokość stojaków i ramiaków ościeżnicy – bmos = btos = 0,035 m.
Rozwiązanie składa się z czterech kroków:
- Obliczamy wg wzoru (7) szerokość poszczególnych skrzydeł bskr:
bskr= (2,40 – 2 · 0,035 – (3 – 1) · 0,02) / 3= 0,763 m; - Obliczamy wg wzoru (8) wysokość poszczególnych skrzydeł hskr:
hskr = (1,48 – 2 · 0,035 – (2 – 1) · 0,02) / 2 = 0,695 m; - Obliczamy wg wzoru (2) pole powierzchni oszklenia Ag:
Ag = (0,763 – 2 · 0,08)(0,695 – 2 · 0,08) · 3 · 2 = 1,936; - Obliczamy wartość wskaźnika C:
C = Ag /Ao = 1,936 / 3,552 = 0,545.
Wnioski
- Za pomocą opracowanego modelu matematycznego oszacowano efekty wpływu parametrów wieloskrzydłowych okien o zmiennej konfiguracji na udział pola powierzchni szklonej do całkowitego pola powierzchni okna C, charakteryzujący warunki dopływu energii słonecznej do wnętrza budynku.
- Wykryto, że wskaźnik C nawet dla okien 1-skrzydłowych istotnie różni się od zalecanej wartości C = 0,7 [–], ponieważ wahania czynników (pola powierzchni okien i szerokości elementów ramy skrzydłowej) w przyjętym w badaniu zakresie zmienności różnicują wartość wskaźnika C od 0,512 do 0,808 [–]. Dla okien wieloskrzydłowych wskaźnik C całkiem odbiega od wartości zalecanej i należy go obliczać, uwzględniając parametry okna.
- Zaproponowano wzory i algorytm obliczeń udziału pola powierzchni szklonej do całkowitego pola powierzchni wieloskrzydłowych okien o zmiennej konfiguracji.
Literatura
- Rozporządzenie Ministra Infrastruktury i Rozwoju z dnia 27 lutego 2015 r. w sprawie metodologii wyznaczania charakterystyki energetycznej budynku lub części budynku oraz świadectw charakterystyki energetycznej (DzU 2015 poz. 376).
- PN-EN 410:2001, "Szkło w budownictwie - Określenie świetlnych i słonecznych właściwości oszklenia".
- PN-EN ISO 13790:2008, "Energetyczne właściwości użytkowe budynków - Obliczanie zużycia energii do ogrzewania i chłodzenia”.
- PN-EN 12519:2007, "Okna i drzwi. Terminologia".
- J. Gutenbaum, "Modelowanie matematyczne systemów", Wydawnictwo EXIT, Warszawa 2003.
- M. Korzyński, "Metodyka eksperymentu. Planowanie, realizacja i statystyczne opracowanie wyników eksperymentów technologicznych", WNT, Warszawa 2006.
- B. Durakovic, "Design of Experiments Application, Concepts, Examples: State of the Art", "Periodicals of Engineering and Natural Sciences", vol. 5/2017, no. 3: 421-439.