Wpływ sposobu osadzania stolarki okiennej na współczynnik przenoszenia ciepła ściany osłonowej z oknem

To, jak okno zostanie zamontowane, wpływa na bilans energetyczny całego budynku.
Ytong
Osadzenie okna w ścianie zewnętrznej nie jest czynnością trudną technicznie, zwłaszcza dla fachowców. Jednakże trzeba pamiętać, że to, jak okno zostanie zamontowane, wpływa na bilans energetyczny całego budynku. Dzieje się tak dlatego, że na wartość bilansu oddziałują nie tylko właściwości samego okna, duże znaczenie ma również utworzone połączenie na styku ościeżnica–ościeże okna. Ciągle udoskonala się metody montażu okien w ścianach, by w możliwie największym stopniu zmniejszyć wpływ liniowego mostka cieplnego po obwodzie ramy okiennej i możliwie najbardziej zredukować wartość liniowego współczynnika przenikania ciepła ψ tego mostka.
Zobacz także
BREVIS S.C. Czy nawiewniki w oknach są obowiązkowe – najważniejsze Informacje

Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu...
Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu uniknięcia negatywnych skutków zbyt dużej wilgotności, to już dyskomfort siedzenia w dusznym i nieprzewietrzonym pomieszczeniu zna każdy. Oprócz wentylacji grawitacyjnej do niedawna odpowiednią cyrkulację powietrza zapewniały nieszczelności w oknach. Jednak rozwój technologiczny i zwiększenie szczelności...
DAKO Jak wybrać drzwi do nowoczesnego domu?

Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie...
Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie aspekty trzeba zwrócić szczególną uwagę, wybierając drzwi zewnętrzne!
RoletyAlu Sp. z o.o. Jak łatwo kupić rolety zewnętrzne przez internet?

Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość...
Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość złożenia zamówienia bezpośrednio u producenta rolet zewnętrznych pozwala wyeliminować pośredników, co skraca czas potrzeby na realizację zamówień i przekłada się na dużo niższe ceny.
Abstrakt |
|---|
|
W artykule przeanalizowano wpływ sposobu osadzania stolarki okiennej, scharakteryzowanego liniowym współczynnikiem przenikania ciepła mostka cieplnego na granicy rama–ściana, na współczynnik przenoszenia ciepła ściany osłonowej z oknem o zmiennej powierzchni i konfiguracji, wykonanym z PVC. Zbiór danych do analizy uzyskano przy realizacji eksperymentu obliczeniowego. Analiza wykonana została na podstawie opracowanego deterministycznego modelu matematycznego opisującego tę zależność. Informacja może być przydatna dla projektantów, naukowców, producentów i konsumentów stolarki okiennej. The influence of the installation of window frames on the heat transfer coefficient of the curtain wall with the windowThe article analyses the influence of the manner of the installation of window frames, characterised by a linear heat transfer coefficient curve of a thermal bridge on the frame-wall boundary, on the heat transfer coefficient of the curtain wall with a PVC window with a variable surface area and configuration. The data set for the analysis was obtained in course of the implementation of a computational experiment. The analysis was made on the basis of a developed deterministic mathematical model describing this relationship. This information can be useful for designers, scientists, producers and consumers of window frames. |
Problem liniowych mostków termicznych należy rozwiązać już na etapie projektowania budynku. Zminimalizowanie liczby mostków w konstrukcji można osiągnąć poprzez uniknięcie uszkodzenia warstwy izolacji w przegrodach zewnętrznych i na ich połączeniach [1]. Ważne jest także prawidłowe umiejscowienie okien w ścianach. W tym celu należy poprawnie wybrać miejsce montażu okna w przegrodzie (w zależności od jej konstrukcji), później należy wykorzystać odpowiednie materiały izolacyjne i uszczelniające, a zakończyć na ich właściwym wykorzystaniu.
Zgodnie z zaleceniami Krajowej Agencji Poszanowania Energii [1] okna w ścianie zewnętrznej można osadzać w następujący sposób:
- w ścianie trójwarstwowej z izolacją cieplną wewnątrz - w strefie warstwy dociepleniowej,
- w ścianie dwuwarstwowej i izolacją termiczną na zewnątrz muru - przed licem muru lub w licu muru,
- w ścianie pełnej (jednowarstwowej) bez izolacji cieplnej - w połowie grubości przegrody.
Do oceny doskonałości utworzonego połączenia na styku ościeżnica–ościeże okna należy dokładnie określić wartość liniowego współczynnika przenikania ciepła ψ. W tym celu stosuje się albo specjalistyczne programy komputerowe, albo katalogi mostków cieplnych. Metodyka obliczeń stosowana w programach komputerowych powinna być zgodna z normą PN-EN ISO 10211 [2]. Ważne, by nie operować wartościami zawartymi w normie PN-EN ISO 14683 [3], gdyż mają one charakter orientacyjny i są obarczone bardzo dużym błędem (nawet do 50%) [1].
Do tej pory do obliczeń współczynnika ψ liniowych mostków termicznych stosowało się program EUROKOBRA. W pracy Prusakiewicza [4] podano przykład obliczenia dla stolarki okiennej w warstwie izolacji oraz z izolacją nachodzącą na ramę okienną, dla którego współczynnik ψ wynosi 0,01 W/(m·K).
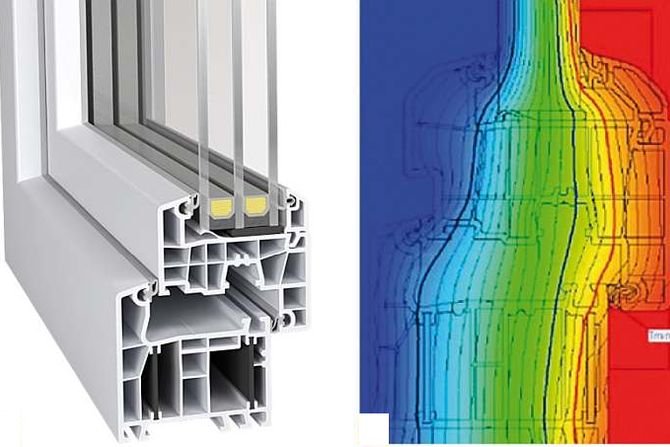
Do obliczeń mostków termicznych z wykorzystaniem założeń normy PN-EN ISO 10211 [2] należy stosować program Therm. Według Krajowej Agencji Poszanowania Energii [1] dla okna zmontowanego równo z zewnętrzną krawędzią ściany nośnej z izolacją, która nachodzi na ramę okienną na 3-4 cm (RYS. 1-3), obliczenia za pomocą programu Therm pozwoliły uzyskać współczynnik ψ na poziomie 0,023 W/(m·K). Natomiast dla okna zmontowanego w warstwie izolacji poza ścianą nośną, gdzie izolacja nachodzi na ramę okienną na ok. 3-4 cm (RYS. 4-6), wartość współczynnika ψ wynosi nawet do 0,008 W/(m·K) [1].
![RYS. 1-3. Warianty osadzania stolarki okiennej: okno zmontowane równo z zewnętrzną krawędzią ściany nośnej, izolacja cieplna nachodzi na ramę okienną na ok. 3-4 cm: model (1), izotermy (2), rozkład temperatur (3); rys.: [1] RYS. 1-3. Warianty osadzania stolarki okiennej: okno zmontowane równo z zewnętrzną krawędzią ściany nośnej, izolacja cieplna nachodzi na ramę okienną na ok. 3-4 cm: model (1), izotermy (2), rozkład temperatur (3); rys.: [1]](https://www.izolacje.com.pl/media/cache/typical_view/data/202011/b-wplyw-sposobu-osadzania-rys1-3.jpg)
RYS. 1-3. Warianty osadzania stolarki okiennej: okno zmontowane równo z zewnętrzną krawędzią ściany nośnej, izolacja cieplna nachodzi na ramę okienną na ok. 3-4 cm: model (1), izotermy (2), rozkład temperatur (3); rys.: [1]
![RYS. 4-6. Warianty osadzania stolarki okiennej: okno zmontowane w warstwie izolacji termicznej poza ścianą nośną; izolacja nachodzi na ramę okienną na 3-4 cm: model (4), izotermy (5), rozkład temperatur (6); rys.: [1] RYS. 4-6. Warianty osadzania stolarki okiennej: okno zmontowane w warstwie izolacji termicznej poza ścianą nośną; izolacja nachodzi na ramę okienną na 3-4 cm: model (4), izotermy (5), rozkład temperatur (6); rys.: [1]](https://www.izolacje.com.pl/media/cache/typical_view/data/202011/b-wplyw-sposobu-osadzania-rys4-6.jpg)
RYS. 4-6. Warianty osadzania stolarki okiennej: okno zmontowane w warstwie izolacji termicznej poza ścianą nośną; izolacja nachodzi na ramę okienną na 3-4 cm: model (4), izotermy (5), rozkład temperatur (6); rys.: [1]
Jak widać z przytoczonych danych, podstawowy parametr charakteryzujący sposób osadzania okien wykonanych z PCV, czyli liniowy współczynnik przenikania ciepła ψ, waha się w wąskim zakresie na poziomie 0,008-0,023 W/(m·K). Niestety, do tej pory nie przedstawiono ogólnie dostępnych badań, w których zostałby oszacowany wpływ powstałych liniowych mostków cieplnych na granicy ościeżnica–ościeże na przenoszenie ciepła w ścianach zewnętrznych. Jest to ważna kwestia, wpływająca na końcowy bilans energetyczny całego budynku, zatem należy ją poddać rozważaniom.
Dlatego też celem niniejszego opracowania jest analiza wpływu sposobu osadzania stolarki okiennej, scharakteryzowanego liniowym współczynnikiem przenikania ciepła mostka termicznego na granicy rama–ściana, na współczynnik przenoszenia ciepła ściany osłonowej z oknem o zmiennej powierzchni i konfiguracji, wykonanym z PVC. Analiza wykonana została na podstawie opracowanego deterministycznego modelu matematycznego opisującego tę zależność.
Metoda obliczania współczynnika przenoszenia ciepła
Współczynnik przenoszenia ciepła przez przenikanie ze strefy ogrzewanej do środowiska zewnętrznego w przegrodach budowlanych jest jedną z najważniejszych wielkości przy obliczeniach zapotrzebowania ciepła na energię użytkową w budynkach ogrzewanych. Charakteryzuje on przenoszenie ciepła przez fragment przegrody z polem powierzchni Aw, zawierający kilka elementów składowych. Dla ściany osłonowej z oknem, według PN-EN ISO 13789:2008 [5], współczynnik ten można obliczyć ze wzoru:
![]() (1)
(1)
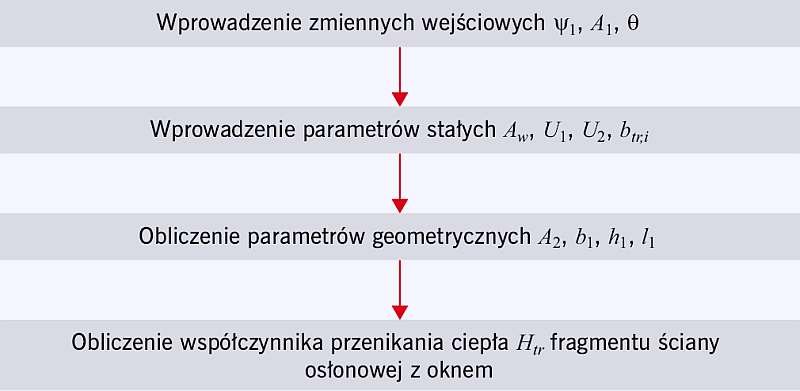
RYS. 7. Schemat blokowy obliczania współczynnika przenoszenia ciepła Htr, gdzie: A1, A2, Aw - powierzchnia, odpowiednio: okna; ściany pełnej; ściany osłonowej z oknem; h1 - wysokość okna; b1 - szerokość okna; θ - proporcja okna; ψ1 – liniowy współczynnik przenikania ciepła mostka liniowego na styku ramy okiennej i ściany pełnej; l1 - długość mostka liniowego na styku ramy okiennej i ściany pełnej; U1, U2 - współczynnik przenikania ciepła, odpowiednio, okna; ściany pełnej; btr,i - współczynnik redukcyjny obliczeniowej różnicy temperatur (przyjęto btr,i = 1); rys.: archiwa autorów
gdzie:
btr,i - współczynnik redukcyjny obliczeniowej różnicy temperatur,
Ai - pole powierzchni i-tej przegrody, [m2],
Ui - współczynnik przenikania ciepła i-tej przegrody, [W/(m2 · K)],
li - długość i-tego liniowego mostka cieplnego, [m],
ψi - liniowy współczynnik przenikania ciepła i-tego mostka liniowego, [W/(m·K)].
Z uwzględnieniem celu badania, elementów składowych ściany osłonowej z oknem i wzoru (1), dla określenia współczynnika przenoszenia ciepła Htr w eksperymencie obliczeniowym autorzy wybrali trzy zmienne wejściowe i stworzyli algorytm, którego schemat blokowy pokazano na RYS. 7. Algorytm ten posłużył jako podstawa do opracowania autorskiego programu.
Badane warianty ściany osłonowej z oknem
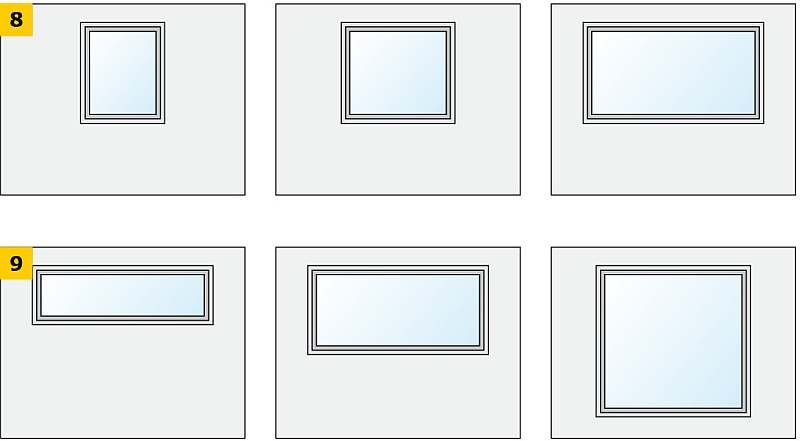
RYS. 8-9. Schematy badanych wariantów ściany osłonowej z oknem ze zróżnicowanym polem powierzchni (8) oraz ze zróżnicowanymi proporcjami wymiarów (9); rys.: archiwa autorów
Rozmiary współczesnych okien ograniczone są gabarytami pomieszczeń. Współczesne technologie montażu stolarki okiennej z PVC pozwalają stosować okna z szerokim zakresem zmienności ich rozmiarów i proporcji.
W badaniu jako fragment ściany osłonowej przyjęto odcinek ściany o rozmiarze 2,70×3,60 = 9,72 m2.
Z uwzględnieniem najczęściej stosowanych rozmiarów okien zostały wybrane następujące warianty stolarki okiennej:
- powierzchnia - od 1,20 m2 do 3,60 m2;
- proporcje (stosunek wysokości okna do jego szerokości) - od 0,3333 do 1.
Liczba skrzydeł nie miała znaczenia, ponieważ wpływają one na współczynnik przenikania ciepła okna, który przyjęto w badaniu jako parametr stały. Schematy badanych wariantów okien podano na RYS. 8-9.
Model matematyczny współczynnika przenoszenia ciepła ściany osłonowej z oknem
Z uwzględnieniem przyjętego celu badania jako funkcję celu Y wybrano współczynnik przenoszenia ciepła przez przenikanie ściany osłonowej z oknem Htr, [W/K].
Przy wyborze czynników, na podstawie wstępnej analizy, wytypowano najważniejsze z nich, opisujące badaną właściwość oraz zapewniające uzyskanie informacji interesującej odbiorców stolarki okiennej. Przeanalizowano również podstawowe wymagania, jakie powinny spełniać czynniki - powinny być sterowalne, jednoznaczne, niesprzeczne i wzajemnie niezależne [6].
Po wstępnej analizie do badania współczynnika Htr przyjęto następujące czynniki:
- ψ1 - liniowy współczynnik przenikania ciepła mostka liniowego na styku ramy okiennej i ściany pełnej (czynnik X1);
- pole powierzchni okna A1(czynnik X2);
- proporcje okna θ, wyrażone stosunkiem wysokości okna do jego szerokości (czynnik X3).
Te czynniki określają wkład w Htr od mostka cieplnego, powstałego po osadzaniu stolarki okiennej. Wkład ten kształtuje się bezpośrednio poprzez ψ1 lub pośrednio przez A1, θ, które wpływają na długość mostka liniowego na styku ramy okiennej i ściany pełnej. Przypuszczano, że szukaną zależność Y = ƒ (X1, X2, X3) może opisywać wielomian drugiego stopnia.
Do uzyskania danych dla opisu tej zależności przeprowadzono 3-czynnikowy eksperyment obliczeniowy według planu drugiego stopnia (TABELA). Zastosowano kompozycyjny symetryczny trójpoziomowy D-optymalny plan B3, zawierający 14 prób [7].
Do wyliczenia wartości Yi w 14 wierszach planu wykorzystano oprogramowanie Microsoft Excel.
Przed rozpoczęciem obliczeń wykonano uzasadniony wybór zakresu zmienności czynników oraz wartości parametrów stałych, od których także zależą efekty wpływu rozpatrywanych czynników.
Liniowy współczynnik przenikania ciepła mostka na styku ramy okiennej i ściany pełnej ψ1 (czynnik X1) na dolnym poziomie przyjęto: 0,005 W/(m·K). Jako górny poziom przyjęto wartość 0,025 W/(m·K). Na średnim poziomie czynnik X1 przyjęto 0,015 W/(m·K).
Wybrany zakres obejmuje liniowe współczynniki przenikania ciepła mostków dla przytoczonych wyżej sposobów osadzania stolarki okiennej (RYS. 1-3).
Przyjęto, że pole powierzchni okna A1 (czynnik X2) na dolnym poziomie wynosi 1,20 m2. Jako górny poziom przyjęto powierzchnię okna trzykrotnie zwiększoną - 3,60 m2. Odpowiednio na średnim poziomie przyjęto 2,40 m2.
Proporcje okien, wyrażone stosunkiem wysokości do szerokości okna θ (czynnik X3), przyjęto na poziomach 0,3333; 0,6667; 1,0 [–]. Pozwala to rozpatrywać okna w dużej rozpiętości zmiany ich zarysu zewnętrznego - od prostokąta z proporcją 1:3 do kwadratu z proporcją 1:1.
Pozostałe wielkości geometryczne wymienione we wzorze (1) wyliczano na podstawie wartości wybranych czynników.
Wartości współczynników przenikania ciepła okna U1 i ściany pełnej U2 przyjęto na obecnym poziomie wymagań ochrony cieplnej, tj. U1= 1,10; U2 = 0,23 W/(m2·K).
Wymienione wyżej wartości naturalne czynników Ẋ1, Ẋ2, Ẋ3 i odpowiadające im wartości unormowane X1, X2, X3 przedstawiono w TABELI. Według Korzyńskiego [7] przejście z wartości naturalnych Ẋi do unormowanych Xi wyraża się wzorem:
![]() (2)
(2)
gdzie:
Ẋi, Ẋimax, Ẋimin - odpowiednio bieżące, maksymalne i minimalne wartości naturalne i-tego czynnika.
Na podstawie wyników obliczeń (TABELA) za pomocą metody najmniejszych kwadratów [7] opracowano równanie regresji zależności Y = ƒ(X1, X2, X3). Istotność współczynników tego równania oceniono za pomocą t-kryterium.
Metoda testowania współczynników została szczegółowo opisana przez autorów w pracy "Parametry cieplne wieloskrzydłowej stolarki okiennej w budynkach mieszkalnych" [8]. W wyniku testu 1 współczynnik okazał się nieistotny. Po ich usunięciu przyjęto postać końcową równania z k + 1 = 9 współczynnikami:
 (3)
(3)
Potwierdzona została również adekwatność uzyskanego modelu według metody opisanej w pracach Korzyńskiego oraz Jezierskiego i Borowskiej [7-8].
Dany model posiadał
- Σ(Yi – Ŷi)2 = 0,00012;
 = Σ(Yi –Ŷi)2/[N – (k +1)] = 0,00003;
= Σ(Yi –Ŷi)2/[N – (k +1)] = 0,00003;- R2 = 0,9999.
Dodatkowo jakość aproksymacji danych opracowanym równaniem oceniono według kryterium F [7].
Przy poziomie istotności α = 0,05 i liczbie stopni swobody
- ƒ1 = N – 1 = 14 – 1 = 13;
- ƒ2 = N – (k + 1) = 14 – 10 = 4
okazało się, że wartość obliczeniowa kryterium F0 = ![]() = 182154,8759 wielokrotnie przekracza wartość tabelaryczną F0,05;23;9 = 5,89 [7], co potwierdza jego wysoką jakość.
= 182154,8759 wielokrotnie przekracza wartość tabelaryczną F0,05;23;9 = 5,89 [7], co potwierdza jego wysoką jakość.
Analiza wyników badania
Za pomocą równania regresji (3) przeanalizowano stopień i charakter wpływu poszczególnych czynników na współczynnik przenoszenia ciepła Htr ściany osłonowej z oknem. Analizę przeprowadzono dla zmiennych w postaci naturalnej. Wykryto, że na współczynnik Htr najmocniejszy niekorzystny wpływ okazuje czynnik X2 - powierzchnia okna A1.
Przy zmianie A1 od 1,20 do 3,60 m2 wartość współczynnika Htr równomiernie wzrasta od 3,346 do 5,486 W/K, tj. o 64,0%. Oznacza to, że dla rozpatrywanych warunków na każdy dodany 1 m2 powierzchni okna, przy średnim poziomie pozostałych zmiennych, współczynnik Htr ściany osłonowej z oknem rośnie równomiernie o około 26,7%.
Również niekorzystny, jednak o 21 razy słabszy wpływ okazuje czynnik X1 - liniowy współczynnik przenikania ciepła mostka termicznego na styku rama-ściana ψ1. Przy zmianie ψ1 od 0,005 do 0,025 [W/(m·K)]wartość współczynnika Htr równomiernie wzrasta od 4,355 do 4,483 W/K, tj. zaledwie o 3,0%. Efekt interakcji w modelu, który został odzwierciedlony współczynnikiem 0,017X1X2, świadczy o tym, że ze wzrostem pola powierzchni okna stopień wpływu współczynnika ψ1 wzrasta.
Odwrotna sytuacja została zaobserwowana dla współczynnika 0,005X1X3; ze wzrostem proporcji okna stopień wpływu współczynnika ψ1 słabnie. Objaśnić to można zmianą w obu przypadkach długości mostka liniowego na styku ramy okiennej i ściany pełnej.
W celu uzyskania dokładniejszej odpowiedzi na pytanie o wpływie sposobu osadzania stolarki okiennej w ścianie osłonowej, za pomocą modelu (3) zastało wykonane obliczenie współczynnika Htr dla wartości ψ1= 0,008 W/(m · K), charakterystycznej według zaleceń Krajowej Agencji Poszanowania Energii [1] dla okna osadzonego w warstwie izolacji poza ścianą nośną, gdzie izolacja nachodzi na ramę okienną na 3-4 cm (sposób 1, RYS. 1-3), oraz ψ1= 0,023 W/(m·K), charakterystycznej według tychże zaleceń [1] dla okna osadzonego równo z zewnętrzną krawędzią ściany nośnej, gdzie izolacja nachodzi na ramę okienną na 3-4 cm (sposób 2, RYS. 4–6).
Wyniki obliczeń wykazały, że dla sposobu pierwszego współczynnik Htr,1 = 4,374 W/K, zaś dla sposobu drugiego Htr,2 = 4,470 W/K. Oznacza to, że różnica efektów od zastosowania tych dwóch sposobów osadzania stolarki wynosi: Htr,2– Htr,1= 0,096 W/K,tj. zastosowanie sposobu pierwszego w porównaniu ze sposobem drugim pozwala obniżyć współczynnik Htr o 2,2%.
Zdaniem autorów wykryty efekt wpływu współczynnika ψ1 jest słaby i może nawet zniechęcić konstruktorów od udoskonalania sposobów osadzania okien. Mimo to nie można jednoznacznie stwierdzić, że jest on nieistotny i jego wpływ może być pomijany. Wszystko zależy od całkowitej powierzchni ściany osłonowej i liczby okien w budynku, od udziału ilości ciepła na ogrzewanie w całkowitym zapotrzebowaniu na ciepło użytkowe.
Sytuacja z oszacowaniem efektu wpływu współczynnika ψ1 będzie różna w jednorodzinnym budynku mieszkalnym (6-8 okien) i budynku wielokondygnacyjnym, np. dla 60 mieszkań (180-240 okien). Ostatni czynnik X3 - proporcje okna θ, wykazał najsłabszy, lecz korzystny wpływ na badaną funkcję.
Przy zmianie θ od 0,3333 do 1,0 współczynnik Htr zmniejsza się od 4,431 do 4,417 W/K, tj. maleje tylko o 0,3%. To znaczy, że nawet w przyjętym rozszerzonym zakresie zmienności czynnik θ nie wykazuje istotnego wpływu na wartość współczynnika Htr.
Z przeprowadzonych dodatkowo obliczeń wynika, że przy zmianie kształtu okna z prostokąta o proporcjach 1:3 do kwadratu 1:1 długość liniowego mostka zmniejsza się o 15,5%. Jednak kilkunastokrotnie mniejsza wartość liniowego współczynnika przenikania ciepła mostka ψ1 w porównaniu z wartościami współczynników przenikania ciepła szkła i ramy ostatecznie osłabia (poprzez iloczyn L1 i ψ1) do 0,3% wkład czynnika θ w obniżenie współczynnika Htr.
Opisany charakter wpływu czynników odzwierciedla wykres na rys. 10, na którym pokazano graficzną zależność Htr = ƒ (A1,ψ1) dla θ = 0,6667.
Wnioski
Opracowany deterministyczny model matematyczny pozwolił dokładnie określić charakter i stopień wpływu wybranych czynników na współczynnik przenoszenia ciepła przez przenikanie ściany osłonowej z oknem Htr.
Na współczynnik Htr największy wpływ wykazuje powierzchnia okna A1, najmniejszy - proporcje okna θ. Wartość współczynnika Htr, przy zmianie czynnika A1 z dolnego do górnego poziomu wzrosła o 64,0%, zaś czynnika θ - zmalała o 0,3%.
Wykryto słaby efekt wpływu liniowego współczynnika przenikania ciepła mostka termicznego na styku rama–ściana ψ1, charakteryzującego sposób osadzania stolarki okiennej.
Zamiana osadzania okna w warstwie izolacji poza ścianą nośną [ψ1= 0,008 W/(m · K)] na osadzanie okna na równo z zewnętrzną krawędzią ściany nośnej [ψ1= 0,023 W/(m · K)] obniża wartość współczynnika Htr tylko o 2,2%. Ostateczna ocena efektu wpływu współczynnika ψ1 zależy od charakterystyk budynku.
Literatura
- Krajowa Agencja Poszanowania Energii SA, "Podręcznik dobrych praktyk”, listopad 2012.
- PN-EN ISO 10211:2008, "Mostki cieplne w budynkach - Strumienie ciepła i temperatury powierzchni – Obliczenia szczegółowe".
- PN-EN ISO 14683:2008, "Mostki cieplne w budynkach - Liniowy współczynnik przenikania ciepła - Metody uproszczone i wartości orientacyjne".
- M. Prusakiewicz, "Katalog mostków cieplnych - budynki niskoenergetyczne i pasywne", praca inżynierska, WIL PW, 2012.
- PN-EN ISO 13789:2008, "Cieplne właściwości użytkowe budynków - Współczynnik przenoszenia ciepła przez przenikanie i wentylację - Metoda obliczania".
- J. Gutenbaum, "Modelowanie matematyczne systemów", Wyd. EXIT, Warszawa 2003.
- M. Korzyński, "Metodyka eksperymentu. Planowanie, realizacja i statystyczne opracowanie wyników eksperymentów technologicznych", WNT, Warszawa 2006.
- W. Jezierski, J. Borowska, "Parametry cieplne wieloskrzydłowej stolarki okiennej w budynkach mieszkalnych", "IZOLACJE" 6/2017, s. 36-40.