Analiza współczynnika przenikania ciepła okna z osłoną przeciwsłoneczną
Analysis of heat transfer coefficient of a window with a sun visor

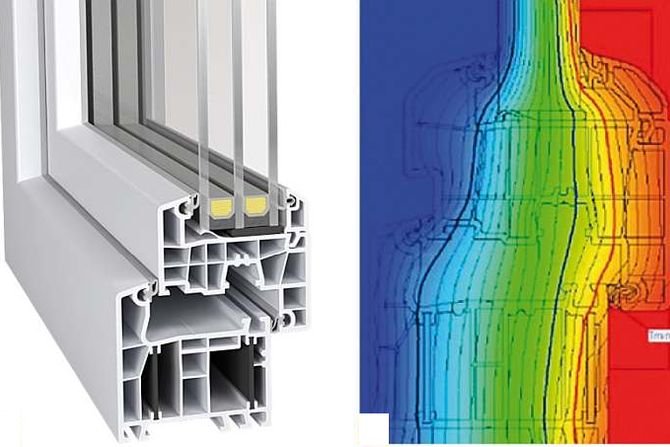
Bardzo ważną rolę w zapewnieniu komfortu cieplnego w pomieszczeniach budynków energooszczędnych spełniają przegrody przezroczyste.
Archiwum redakcji
Jedną z podstawowych potrzeb, jakie należy spełnić w budynkach mieszkalnych, jest zapewnienie mieszkańcom komfortu cieplnego, czyli uzyskanie przez osoby użytkujące pomieszczenia akceptacji dla panujących w nich warunków cieplnych.
Zobacz także
BREVIS S.C. Czy nawiewniki w oknach są obowiązkowe – najważniejsze Informacje

Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu...
Potrzeba zapewnienia właściwej wentylacji domu czy mieszkania nie stanowi raczej zaskoczenia dla nikogo. Choć może nie zawsze mamy na uwadze utrzymanie odpowiedniej wilgotności powietrza i dzięki temu uniknięcia negatywnych skutków zbyt dużej wilgotności, to już dyskomfort siedzenia w dusznym i nieprzewietrzonym pomieszczeniu zna każdy. Oprócz wentylacji grawitacyjnej do niedawna odpowiednią cyrkulację powietrza zapewniały nieszczelności w oknach. Jednak rozwój technologiczny i zwiększenie szczelności...
DAKO Jak wybrać drzwi do nowoczesnego domu?

Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie...
Wybór drzwi wejściowych nie jest łatwym zadaniem. Muszą one wpasowywać się w stylistykę budynku, a przy tym spełniać wszystkie wymagania dotyczące bezpieczeństwa i komfortu użytkowania. Zobacz, na jakie aspekty trzeba zwrócić szczególną uwagę, wybierając drzwi zewnętrzne!
RoletyAlu Sp. z o.o. Jak łatwo kupić rolety zewnętrzne przez internet?

Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość...
Zamawiając rolety zewnętrzne przez internet, można skorzystać z bogatej oferty asortymentu, a dodatkowo zyskać pewność, że zostaną wykonane zgodnie z wymiarami podanymi przez klienta. Dodatkowo możliwość złożenia zamówienia bezpośrednio u producenta rolet zewnętrznych pozwala wyeliminować pośredników, co skraca czas potrzeby na realizację zamówień i przekłada się na dużo niższe ceny.
O czym przeczytasz w artykule? |
Abstrakt |
|---|---|
|
W artykule przeanalizowano współczynnik przenikania ciepła okna z PVC z osłoną przeciwsłoneczną w zależności od typu osłony, scharakteryzowanego wartością dodatkowego oporu cieplnego wynikającego z zastosowania osłony, od pola powierzchni okna, od sposobu połączenia szyby z ramą, scharakteryzowanego wartością liniowego współczynnika przenikania ciepła mostku termicznego powstającego na granicy szyba-rama, oraz współczynników przenikania ciepła oszklenia i ramy. Analysis of heat transfer coefficient of a window with a sun visorThe article contains an analysis of heat transfer coefficient of a PVC window with a sun visor, depending on the type of cover, characterized by the value of additional thermal resistance resulting from the use of a cover, window surface area, pane and frame joint type, characterized by the value of linear thermal transfer coefficient for the thermal bridge on the glass-frame border, as well as heat transfer coefficients of the glazing and the frame. |
Bardzo ważną rolę w zapewnieniu komfortu cieplnego w pomieszczeniach budynków energooszczędnych spełniają przegrody przezroczyste, a także osłony przeciwsłoneczne. Związane jest to z regułą, do której stosują się zarówno inwestorzy, jak i projektanci, że takie budynki lokuje się na działkach z jak największym dostępem do bezpośredniego promieniowania słonecznego. Wówczas na elewacji budynku energooszczędnego stosuje się możliwie dużo przegród przezroczystych – dużych okien, drzwi przeszklonych czy ścian szkieletowych o konstrukcji słupowo-ryglowej wypełnionej oszkleniem. Tylko wtedy możliwe staje się maksymalne wykorzystanie solarnych zysków ciepła w sezonie ogrzewania [1].
W okresie letnim duże przeszklone przegrody, do których dociera nadmierne bezpośrednie promieniowanie słoneczne, wymagają zastosowania osłon przeciwsłonecznych. Ma to na celu uniknięcie przegrzewania pomieszczeń, a w budynkach wyposażonych w odpowiedni system techniczny także ograniczenie zużycia energii na chłodzenie.
W budynkach mieszkalnych jako osłony przeciwsłoneczne można stosować rolety i zasłony, czyli osłony podnoszone bądź opuszczane wzdłuż oszklenia, żaluzje, czyli osłony podnoszone bądź opuszczane wzdłuż oszklenia składające się z listewek o regulowanym kącie nachylenia, a także markizy, czyli zwykle składane zadaszenia, które montuje się nad oknami [1].
W okresie zimowym te same osłony przeciwsłoneczne, rolety lub żaluzje w stanie zamkniętym, który może trwać co najmniej 12 godzin na dobę, stanowią skuteczną barierę dla przepływającego strumienia ciepła. Wartość dodatkowego oporu cieplnego, który jest przypisany dla danej osłony, zależy przede wszystkim od właściwości samej osłony, a także od warstwy powietrza między częścią szkloną okna a osłoną [2].
W TAB. 1 przedstawiono wartości dodatkowego oporu cieplnego wynikającego z zastosowania różnych osłon przeciwsłonecznych umieszczonych po zewnętrznej stronie okna wg normy [3]. Należy zauważyć, że powszechnie stosowane w życiu codziennym „rolety zewnętrzne” w normach i aprobatach technicznych określane są jako „żaluzje zwijane” [2].
![TABELA 1. Wartości dodatkowego oporu cieplnego wynikającego z zastosowania różnych osłon przeciwsłonecznych umieszczonych po zewnętrznej stronie okna zgodnie z PN-EN ISO 10077-1:2007 [3] TABELA 1. Wartości dodatkowego oporu cieplnego wynikającego z zastosowania różnych osłon przeciwsłonecznych umieszczonych po zewnętrznej stronie okna zgodnie z PN-EN ISO 10077-1:2007 [3]](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/b-analiza-wspolczynnika-przenikania-ciepla-okna-tab1.jpg)
TABELA 1. Wartości dodatkowego oporu cieplnego wynikającego z zastosowania różnych osłon przeciwsłonecznych umieszczonych po zewnętrznej stronie okna zgodnie z PN-EN ISO 10077-1:2007 [3]
Niestety w publikacjach naukowych praktycznie nieobecna jest informacja na temat współczynnika przenikania ciepła okna z osłoną przeciwsłoneczną.
Dodatkowy opór cieplny, wynikający z zastosowania wybranej osłony przeciwsłonecznej i podany w [3], nie odzwierciedla całkowitego wpływu tej osłony na współczynnik przenikania ciepła okna z osłoną Uws. Dzieje się tak dlatego, że nie jest uwzględnione wspólne oddziaływanie tego oporu z parametrami fizykalnymi i geometrycznymi okna, nie uściśla się także jego wartości dla okien różnych typów ze zmiennymi rozmiarami oraz o różnych poziomach izolacji cieplnej oszklenia i ramy. Podobna informacja byłaby jednak bardzo przydatna dla projektantów i producentów osłon i stolarki okiennej.
W związku z powyższym celem danego badania jest analiza współczynnika przenikania ciepła okna z PVC z osłoną przeciwsłoneczną w zależności od typu osłony, scharakteryzowanego wielkością dodatkowego oporu cieplnego wynikającego z zastosowania osłony, od pola powierzchni okna, od sposobu połączenia szyby z ramą, scharakteryzowanego wartością liniowego współczynnika przenikania ciepła mostka termicznego powstającego na granicy szyba–rama oraz od współczynników przenikania ciepła oszklenia i ramy. Analiza wykonana została na podstawie opracowanego deterministycznego modelu matematycznego opisującego tę zależność.
Metoda obliczania współczynnika przenikania ciepła okna z osłoną przeciwsłoneczną
Współczynnik przenikania ciepła okna bez uwzględnienia wpływu osłony Uw obliczono metodą składnikową [4]. W metodzie tej dzieli się fragment przegrody na pola powierzchni o różnych właściwościach cieplnych, a całkowity współczynnik przenikania ciepła oblicza się za pomocą ważonych powierzchniowo wartości U elementów składowych.
Według tej metody współczynnik przenikania ciepła Uw pojedynczego jednoskrzydłowego okna można obliczać według wzoru:

gdzie:
Ug, Uƒ, Umtos – współczynniki przenikania ciepła, odpowiednio: oszklenia, ramy, ramiaków i stojaków ościeżnic,
Ag, Aƒ, Amtos – pole powierzchni, odpowiednio: oszklenia, ramy, stojaków i ramiaków ościeżnic,
Ψg–ƒ, Ψm–ƒ, Ψt–ƒ – liniowe współczynniki przenikania ciepła mostków termicznych powstających na granicy szyba–rama, rama–stojaki ościeżnic i rama–ramiaki ościeżnic,
lg–ƒ, lm–ƒ, lt–ƒ – długości liniowych mostków termicznych powstających na styku szyba–rama, rama–stojaki ościeżnic i rama–ramiaki ościeżnic.
Wartości pól powierzchni Ag, A ƒ, Amtos oraz długości mostków lg–ƒ, lm–ƒ, lt–ƒ mogą być określone ze wzorów opracowanych przez autorów:

gdzie:
bo, bskr, bƒ, bmos, btos – szerokość, odpowiednio: okna, skrzydła, elementów ramy, stojaków i ramiaków ościeżnic.
Do obliczenia współczynnika przenikania ciepła okna z uwzględnieniem efektu osłon przeciwsłonecznych Uws zastosowano model obliczeniowy podany w normie [3], według którego osłonę rozpatruje się jako element dodatkowy i uwzględnia się we wzorze w następujący sposób:

gdzie:
Uw – współczynnik przenikania ciepła okna bez uwzględnienia wpływu osłony przeciwsłonecznej, [W/(m2·K)],
ΔR – wartość dodatkowego oporu cieplnego dla osłony przeciwsłonecznej, [(m2·K)/W].
Wartości dodatkowego oporu cieplnego ΔR, wynikającego z zastosowania różnych osłon przeciwsłonecznych umieszczonych po zewnętrznej stronie okna, w tym badaniu przyjmowano zgodnie z załącznikiem G normy [3] w zależności od typu i materiału, z jakiego jest wykonana osłona oraz jej przepuszczalności powietrza.
Dla realizacji eksperymentu obliczeniowego związanego z określeniem szukanego współczynnika przenikania ciepła okien Uws przy zmianie wartości wybranych czynników autorzy stworzyli algorytm do wyliczania (RYS. 1), który stanowił podstawę do opracowania autorskiego programu w Microsoft Excel.

RYS. 1. Schemat blokowy obliczania współczynnika przenikania ciepła Uws okna z osłoną przeciwsłoneczną; rys.: W. Jezierski, J. Borowska
Opis badanego obiektu
Współczesne technologie montażu stolarki okiennej z PVC pozwalają stosować okna z szerokim zakresem zmienności proporcji. W badaniu, z uwzględnieniem najczęściej stosowanych rozmiarów okien w budynkach mieszkalnych, zostały wybrane warianty stolarki okiennej z powierzchnią od 1,20 m2 do 3,60 m2.
Wysokość okien przyjęto jako parametr stały równy 1,48 m. Schematy badanych wariantów okna podano na RYS. 2.
Dla badanych okien po ich zewnętrznej stronie przewidziano osłonę przeciwsłoneczną zwijaną drewnianą z wypełnieniem pianką w trzech wariantach: o bardzo wysokiej przepuszczalności (wartość dodatkowego oporu cieplnego ΔR = 0,080 (m2·K)/W), o średniej przepuszczalności (ΔR = 0,1925 (m2·K)/W) i szczelną (ΔR = 0,3125 (m2·K)/W) [3].
Model matematyczny współczynnika przenikania ciepła okna z osłoną przeciwsłoneczną
Do osiągnięcia sformułowanego celu jako metodę badawczą zastosowano modelowanie matematyczne, które pozwalają za pośrednictwem zależności matematycznych opisywać funkcjonowanie badanego obiektu, określać parametry wyjściowe, wykonywać poszukiwanie optymalnych wartości parametrów obiektu [5]. Stosowanie modelowania matematycznego pozwala zrezygnować z modelowania fizycznego, skrócić objętość próbkowania, obniżyć pracochłonność badania. Głównym komponentem w takim układzie jest model matematyczny.
Przy opracowaniu modelu matematycznego dąży się do jego praktycznej utylitarności oraz skuteczności. Takie cechy można osiągnąć opracowując krótkie modele, w których wykorzystano najważniejsze czynniki interesujące odbiorców stolarki okiennej.
Zgodnie z przyjętym celem badania jako funkcję celu Y wybrano współczynnik przenikania ciepła okna z osłoną przeciwsłoneczną Uws [W/(m2·K)]. Przy wyborze czynników na podstawie wstępnej analizy wytypowano najważniejsze z nich, wpływające na Uws oraz zapewniające uzyskanie informacji interesującej odbiorców stolarki okiennej.
Przeanalizowano również spełnienie podstawowych wymagań stawianych czynnikom – powinny one być sterowalne, jednoznaczne, niesprzeczne i wzajemnie niezależne [5].
Po analizie do badania przyjęto zależność współczynnika przenikania ciepła Uws (Y) od następujących czynników: dodatkowego oporu cieplnego dla odpowiedniego typu osłon ΔR (czynnik X1), pola powierzchni okna Ao (czynnik X2), liniowego współczynnika przenikania ciepła mostka termicznego na granicy szyba–rama Ψg–ƒ (czynnik X3), współczynnika przenikania ciepła oszklenia Ug (czynnik X4). współczynnika przenikania ciepła ramy Uƒ(czynnik X5).
Przypuszczano, że szukaną zależność Y = ƒ(X1, X2, X3, X4, X5) może opisywać wielomian drugiego stopnia w postaci:

Do uzyskania danych dla opisu tej zależności przeprowadzono 5-czynnikowy eksperyment obliczeniowy według planu drugiego stopnia (TAB. 2). Zastosowano kompozycyjny symetryczny trójpoziomowy plan zawierający 26 prób [6]. Do wyliczenia wartości Yi w 26 wierszach planu wykorzystano oprogramowanie Microsoft Excel.
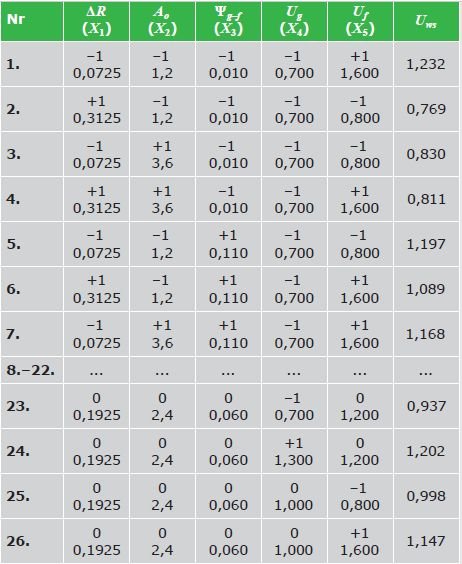
TABELA 2. Macierz planowania i wyniki eksperymentu obliczeniowego do określenia współczynnika przenikania ciepła Uws okna z osłoną przeciwsłoneczną
Przed rozpoczęciem obliczeń wykonano uzasadniony wybór zakresu zmienności czynników. Wielkość dodatkowego oporu cieplnego ΔR dla wybranego typu osłon (czynnik X1) na dolnym poziomie przyjęto 0,0725 (–1), na średnim – 0,1925 (0), na górnym – 0,3125 (+1) (m2·K)/W.
Wybrany zakres zmienności nie w pełnym stopniu odpowiadał wartościom oporów cieplnych dla przytoczonych wyżej wariantów osłony przeciwsłonecznej. Jednak wymaganie z zakresu planowania eksperymentu odnośnie symetrycznych zakresów zmienności dla wszystkich czynników zmusiło autorów do tego, by odstąpić od podanej w [3] wartości 0,080 (X1 = –0,9375) (m2·K)/W oraz zamienić ją na 0,0725 (m2·K)/W. Jednak nie tworzyło to żadnych problemów z modelowaniem ponieważ nowy zwiększony zakres pokrywa poprzednią wartość.
Pole powierzchni okna Ao (czynnik X2) na dolnym poziomie przyjęto równe 1,20 m2 (–1). Jako górny poziom przyjęto powierzchnię okna trzykrotnie zwiększoną 3,60 m2 (+1), odpowiednio na średnim poziomie 2,40 m2 (0).
W celu uniknięcia niejednoznaczności tego czynnika wysokość okien przyjęto jako wartość stałą wynoszącą 1,48 m.
Liniowy współczynnik przenikania ciepła mostka termicznego na granicy szyba–rama Ψƒ–g został przyjęty na poziomach: dolnym 0,010 W/(m·K) (–1), średnim 0,060 W/(m·K) (0), górnym 0,110 W/(m·K) (+1).
Współczynnik przenikania ciepła oszklenia Ug (czynnik X4) na poziomie średnim przyjęto 1,0 W/(m2·K) (0), na poziomie górnym 1,30 W/(m2·K) (+1), a na poziomie dolnym 0,70 W/(m2·K) (–1).
Współczynnik przenikania ciepła ramy Uƒ (czynnik X5) na poziomie średnim przyjęto 1,20 W/(m2·K) (0), na poziomie górnym 1,60 W/(m2·K) (+1), a na poziomie dolnym 0,80 W/(m2·K) (–1).
Pozostałe parametry przyjęto na stałym poziomie: szerokość elementów ramy bƒ= 0,090 m, szerokość stojaków i ramiaków ościeżnic bmos = btos = 0,035 m [7]. Współczynnik przenikania ciepła elementów ościeżnic Umtos przyjęto jako równy współczynnikowi Uƒ. Liniowe współczynniki przenikania ciepła mostków termicznych przyjęto według [8]: Ψm–ƒ = 0,068, Ψt–ƒ = 0,065 W/(m·K).
Wyżej wymienione wartości naturalne czynników ![]() i odpowiadające im wartości unormowane X1, X2, X3, X4, X5 (w nawiasach) przedstawiono w TAB. 2.
i odpowiadające im wartości unormowane X1, X2, X3, X4, X5 (w nawiasach) przedstawiono w TAB. 2.
Przejście z wartości naturalnych do unormowanych Xi według [6] wyraża się wzorem:

gdzie: ![]() odpowiednio bieżące, maksymalne i minimalne wartości naturalne i-tego czynnika.
odpowiednio bieżące, maksymalne i minimalne wartości naturalne i-tego czynnika.
Na podstawie wyników obliczeń (TAB. 2) za pomocą metody najmniejszych kwadratów [9] opracowano równanie regresji zależności Y = ƒ(X1, X2, X3, X4, X5). Istotność współczynników tego równania oceniono za pomocą t-kryterium. Metoda testowania współczynników została szczegółowo opisana przez autorów w [10].
W wyniku testu 5 współczynników okazało się nieistotnych. Po ich usunięciu przyjęto postać końcową równania z k + 1 = 16 współczynnikami:

Potwierdzona została również adekwatność uzyskanego modelu według metody opisanej w [9]. Dany model posiadał:
![]() = 0,0441, R2 = 0,9993. Dodatkowo jakość aproksymacji danych opracowanym równaniem oceniono według kryterium F [9]. Przy poziomie istotności α = 0,05 i liczbie stopni swobody:
= 0,0441, R2 = 0,9993. Dodatkowo jakość aproksymacji danych opracowanym równaniem oceniono według kryterium F [9]. Przy poziomie istotności α = 0,05 i liczbie stopni swobody:
ƒ1 = N – 1 = 26 – 1 = 25,
ƒ2 = N – (k + 1) = 26 – 16 = 10
okazało się, że wartość obliczeniowa kryterium F0 = ![]() = 276,8513 wielokrotnie przekracza wartość tabelaryczną F0,05;25;10 = 2,73 [9], co potwierdza wysoką jakość modelu.
= 276,8513 wielokrotnie przekracza wartość tabelaryczną F0,05;25;10 = 2,73 [9], co potwierdza wysoką jakość modelu.
Analiza wyników badania
Za pomocą równania regresji (13) przeanalizowano stopień i charakter wpływu poszczególnych czynników na współczynnik przenikania ciepła Uws okna z osłoną przeciwsłoneczną. Analizę przeprowadzono dla zmiennych w postaci naturalnej. Interesował autorów przede wszystkim wpływ czynnika X1, czyli dodatkowego oporu cieplnego dla odpowiedniego typu osłon ΔR, wybranego w badaniu jako główny parametr charakteryzujący wpływ osłony przeciwsłonecznej na wielkość współczynnika Uws.
Analizując opracowany model, wykryto, że w centrum Gp przestrzeni czynnikowej, która charakteryzuje się współrzędnymi ΔR = 0,1925 m2·K/W, Ao = 2,40 m2, Ψƒ–g = 0,06 W/(m·K), Ug = 1,00, Uƒ = 1,20 W/(m2·K) wielkość Uws wynosi 1,073 W/(m2·K).
Wykorzystując punkt Gp jako punkt odniesienia, oszacowano wpływ poszczególnych czynników. Okazało się, że korzystny wpływ na wielkość Uws wykazują dwa czynniki: ΔR(X1) oraz Ao(X2). Przy zmianie ich wartości od –1 do +1 następuje zmniejszenie współczynnika Uws o 24,1% dla ΔR(X1) oraz o 11,1% dla Ao(X2).
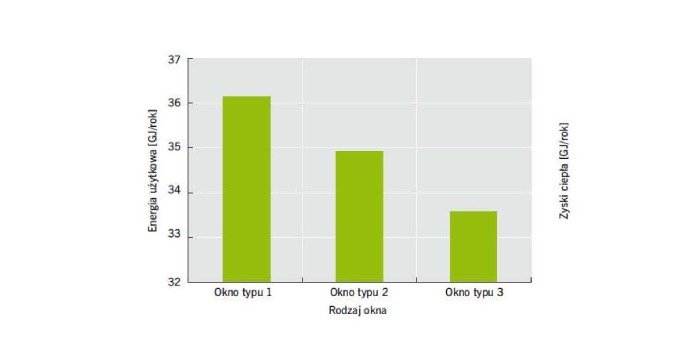
Pozostałe czynniki wykazują wpływ niekorzystny – wraz z ich wzrostem od dolnego do górnego poziomu wielkość współczynnika Uws rośnie o 15,7% dla Ψƒ–g(X3), o 27,8% dla Ug(X4), o 17,6% dla Uƒ(X5). Opisany charakter wpływu czynników odzwierciedla również wykres (RYS. 3), na którym pokazano graficzną zależność Uws = ƒ(ΔR, Ao) dla Ψƒ–g = 0,06 W/(m·K), Ug = 0,70, Uƒ = 1,10 W/(m2·K).
![RYS. 3. Zależność współczynnika przenikania ciepła okna Uws [W/(m2·K)] od dodatkowego oporu cieplnego osłony przeciwsłonecznej ΔR, [(m2·K)/W] oraz pola powierzchni okna Ao, [m2] przy liniowym współczynniku przenikania ciepła mostka termicznego na granicy szyba-rama Ψƒ–g = 0,060 W/(m·K) oraz współczynnikach przenikania ciepła oszklenia Ug = 1,0 i ramy Uƒ = 1,20 W/(m2·K; rys.: W. Jezierski, J. Borowska RYS. 3. Zależność współczynnika przenikania ciepła okna Uws [W/(m2·K)] od dodatkowego oporu cieplnego osłony przeciwsłonecznej ΔR, [(m2·K)/W] oraz pola powierzchni okna Ao, [m2] przy liniowym współczynniku przenikania ciepła mostka termicznego na granicy szyba-rama Ψƒ–g = 0,060 W/(m·K) oraz współczynnikach przenikania ciepła oszklenia Ug = 1,0 i ramy Uƒ = 1,20 W/(m2·K; rys.: W. Jezierski, J. Borowska](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/b-analiza-wspolczynnika-przenikania-ciepla-okna-rys3.jpg)
RYS. 3. Zależność współczynnika przenikania ciepła okna Uws [W/(m2·K)] od dodatkowego oporu cieplnego osłony przeciwsłonecznej ΔR, [(m2·K)/W] oraz pola powierzchni okna Ao, [m2] przy liniowym współczynniku przenikania ciepła mostka termicznego na granicy szyba-rama Ψƒ–g = 0,060 W/(m·K) oraz współczynnikach przenikania ciepła oszklenia Ug = 1,0 i ramy Uƒ = 1,20 W/(m2·K; rys.: W. Jezierski, J. Borowska
Najbardziej dokładnie został poddany analizie wpływ szukanego czynnika ΔR(X1). Zauważono, że w modelu (13) jest kilka efektów interakcji tego czynnika z innymi czynnikami (+0,017X1X2, –0,020X1X3, –0,032X1X4, –0,023X1X5). Analizując te efekty wykryto, że korzystny wpływ czynnika X1 wzmacnia się ze wzrostem czynników X3, X4, X5 oraz słabnie ze wzrostem X2. Dla pełnego przeanalizowania X1 należało oszacować jego wpływ przy odpowiednich skrajnych wartościach X2, X3, X4, X5, które są ograniczone przyjętym w badaniu zakresem zmienności. Po podstawieniach wartości tych czynników do modelu (13) i wykonaniu obliczeń symulacyjnych wykryto dodatkową informację o wpływie czynnika ΔR(X1).
Okazało się, że dla okna z polem powierzchni Ao = 3,60 m2, Ψƒ–g = 0,010 W/(m·K), Ug = 0,7 i Uƒ = 0,8 W/(m2·K) zmiana czynnika ΔR(X1) z 0,0725 do 0,3125 (m2·K)/W powoduje obniżenie współczynnika Uws od 0,855 do 0,739 W/(m2·K), tj. spadek o 13,6%. Natomiast dla okna z polem powierzchni Ao = 1,20 m2, Ψƒ–g = 0,110 W/(m·K), Ug = 1,3 i Uƒ = 1,6 W/(m2·K) zmiana czynnika ΔR(X1) w tym samym zakresie powoduje obniżenie współczynnika Uws od 1,761 do 1,277 W/m2·K, tj. spadek dwukrotnie większy i wynoszący 27,5%.
Dodatkowo oszacowano wahania współczynnika Uws od czynnika ΔR(X1) w centrum Gp przestrzeni czynnikowej. Wykryto, że zamiana osłony o bardzo wysokiej przepuszczalności (ΔR = 0,080 (m2·K)/W) na osłonę szczelną (ΔR = 0,3125 (m2·K)/W) dla okna z polem powierzchni Ao = 2,40 m2 oraz parametrami cieplnymi Ψƒ–g = 0,060 W/(m·K), Ug = 1,0 i Uƒ = 1,2 W/(m2·K) spowoduje obniżenie współczynnika Uws z 1,230 do 0,942 W/m2·K, tj. spadek o 23,4%.
Uzyskane wyniki obliczeń uzupełniają informacje o wpływie osłon przeciwsłonecznych i innych parametrów okien wykonanych z PVC na wielkość ich współczynnika Uws.
Wnioski
- Opracowany deterministyczny model matematyczny pozwolił oszacować charakter i stopień wpływu parametrów okna wykonanego z PVC przy zastosowaniu osłony przeciwsłonecznej zwijanej drewnianej z wypełnieniem pianką o różnej przepuszczalności na współczynnik przenikania ciepła Uws.
- Korzystny wpływ wybranej osłony przeciwsłonecznej na obniżenie wartości Uws wzmacnia się ze wzrostem liniowego współczynnika przenikania ciepła mostka termicznego na granicy szyba–rama Ψƒ–g, współczynników przenikania ciepła oszklenia Ug i ramy Uƒ oraz słabnie ze wzrostem powierzchni okna Ao.
- Zamiana osłony przeciwsłonecznej o bardzo wysokiej przepuszczalności (ΔR = 0,080 (m2·K)/W) na osłonę szczelną (ΔR = 0,3125 (m2·K)/W) dla okna Ao = 2,40 m2, Ψƒ–g = 0,060 W/(mK), Ug = 1,0 i Uƒ = 1,2 W/(m2·K) daje obniżenie współczynnika Uws z 1,230 do 0,942 W/(m2·K), tj. spadek o 23,4%.
Literatura
- R. Geryło, „Współdziałanie przegród przeziernych i osłon przeciwsłonecznych w zapewnieniu komfortu cieplnego”, „Świat Szkła” 4/2015, s. 24–27.
- A. Węglarz, W. Tworek, „Ocena wpływu zastosowania rolet zewnętrznych na współczynnik przenikania ciepła okien. Część 1”. „Polska Energetyka Słoneczna” 1–4/2016, s. 43–46.
- PN-EN ISO 10077-1:2007:2017-101, „Cieplne właściwości użytkowe okien, drzwi i żaluzji. Obliczanie współczynnika przenikania ciepła, Część 1: Postanowienia ogólne”.
- PN-EN ISO 12631:2013-03:2017-10, „Cieplne właściwości użytkowe ścian osłonowych. Obliczanie współczynnika przenikania ciepła”.
- J. Gutenbaum, „Modelowanie matematyczne systemów”, EXIT, Warszawa 2003.
- M. Korzyński, „Metodyka eksperymentu. Planowanie, realizacja i statystyczne opracowanie wyników eksperymentów technologicznych”, WNT, Warszawa 2006.
- A. Błaszczyk, „Systemy okienne. Wiedza techniczna/Instrukcja montażu/Zagadnienia prawne i marketingowe”, Inoutic 2010.
- K. Kasperkiewicz, „Jakość energetyczna okien – wymagania, metody oceny i aktualne możliwości techniczne”, „Materiały Budowlane” 8/2006, s. 53–56.
- B. Durakovic, „Design of Experiments Application, Concepts, Examples: State of the Art”, „Periodicals of Engineering and Natural Sciences” vol. 5/2017 no. 3, s. 421–439.
- W. Jezierski, J. Borowska, „Parametry cieplne wieloskrzydłowej stolarki okiennej w budynkach mieszkalnych”, „Izolacje” 6/2017, s. 36–40.