Stężanie elementów nośnych konstrukcji stalowej za pomocą płyt warstwowych

Wprowadzenie płyt warstwowych do budownictwa istotnie zmieniło sposób kształtowania i wymiarowania stalowych obiektów budowlanych.

Ciężar obudowy stał się nawet o rząd wielkości mniejszy od obciążenia śniegiem, co umożliwiło zmniejszenie ciężaru własnego konstrukcji stalowej przez efektywne ekonomicznie stosowanie elementów o dużych smukłościach ścianek, jak np. profile zimnogięte i blachownice kl. 4.

W Polsce pierwszą linię technologiczną do produkcji płyt z rdzeniem poliuretanowym PW/8 o wydajności do 800 tys. m2 płyt rocznie uruchomiono w 1974 r. w Obornikach Wielkopolskich [1].

Właściwości płyt warstwowych

Płyty warstwowe najczęściej traktowane są jako samonośne elementy obudowy obiektu budowlanego.

W odniesieniu do swej stosunkowo niewielkiej masy charakteryzują się bardzo dobrymi właściwości mechanicznymi.

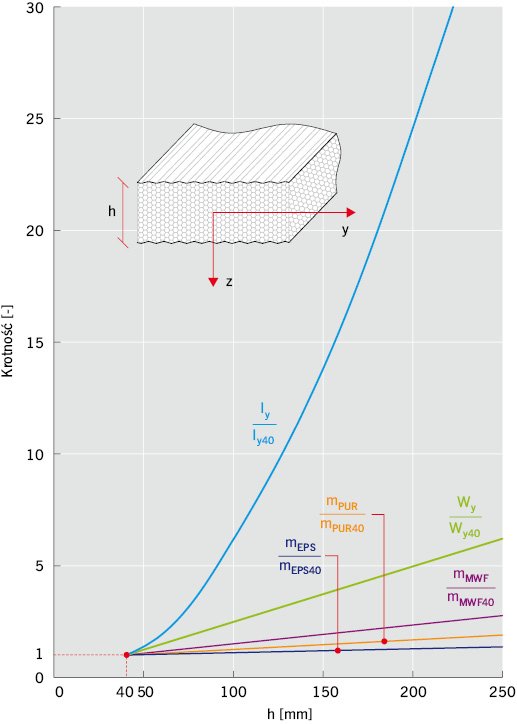
Na RYS. 1 przedstawiono zależność między względnymi przyrostami masy, momentem bezwładności a wskaźnikiem wytrzymałości płyt warstwowych o rdzeniu wykonanym ze styropianu (EPS), poliuretanu (PUR) oraz wełny mineralnej (MWF).

Punktem odniesienia była płyta warstwowa o rozstawie środków ciężkości stalowych blach okładzin (≈ grubości płyty) h = 40 mm.

Można zauważyć, że np. 5-krotne zwiększenie grubości płyty warstwowej o rdzeniu poliuretanowym powoduje przyrost masy płyty m_PUR o zaledwie 68%, podczas gdy wskaźnik wytrzymałości Wy zwiększa się 5-krotnie, a moment bezwładności – ponad 24-krotnie.

W przeciwieństwie do pokryć projektowanych z wykorzystaniem nośnych blach trapezowych płyty warstwowe z reguły nie były wykorzystywane do stężania elementów konstrukcji stalowej (mogło to skutkować zwiększeniem jej ciężaru, a co za tym idzie także kosztu inwestycji).

W wielu przypadkach inwestorzy rezygnowali ze stosowania pokrycia z płyt warstwowych, gdyż niższy koszt montażu płyt warstwowych nie był w stanie zrekompensować zwiększonej ceny konstrukcji stalowej.

Współpraca elementów poszycia ze szkieletem stalowym

Płyty warstwowe oprócz podstawowej funkcji, jaką jest tworzenie przegrody budowlanej o wymaganych parametrach użytkowych, ­takich jak izolacyjność cieplna i akustyczna, bezpieczeństwo pożarowe itd., stanowią elementy mechanicznie współpracujące ze stalowym szkieletem nośnym.

Korzystna zazwyczaj współpraca elementów poszycia z konstrukcją stalową może być wykorzystywana przy ­projektowaniu elementów nośnych i układów konstrukcyjnych i umożliwiać bezpieczną redukcję ich ciężaru.

W normie PN-EN 1993-1-3:2008 [2] zdefiniowano trzy rodzaje współpracy konstrukcji nośnej z elementami poszycia i określono tzw. klasy konstrukcyjne, odpowiadające klasom konsekwencji zniszczenia podanym w normie PN-EN 1990:2004 [3].

Jest to podejście racjonalne, ponieważ włączanie do współpracy elementów nienależących do głównego konstrukcyjnego układu nośnego powoduje zwiększenie jego nośności, a także jest przyczyną transformacji modelu niezawodnościowego układu konstrukcyjnego w kierunku modelu układu szeregowego o wyższym ryzyku zniszczenia.

Wykorzystanie obudowy jako konstrukcyjnego elementu stężającego pozwala na "uprzestrzennienie" modelu statycznego stalowej konstrukcji szkieletu nośnego i na wynikającą z tego (zazwyczaj korzystną)redystrybucję sił wewnętrznych oraz zwiększenie wartości obciążeń krytycznych.

Płyty warstwowe charakteryzują się relatywnie dużą sztywnością, zarówno tarczową, jak i płytową, jednak – w przeciwieństwie do pokrycia z blach trapezowych - ich współpraca z konstrukcją nośną była dotychczas najczęściej pomijana.

Przyczyną tego jest duża odkształcalność połączeń płyt warstwowych oraz ich odmienne (w stosunku do innych połączeń blach cienkich) zachowanie się pod obciążeniem.

Ze względu na wysokość konstrukcyjną płyt warstwowych wkręty samowiercące stosowane do ich łączenia są stosunkowo długie i smukłe (najczęściej średnica trzpienia wkrętu wynosi 5,5 mm), a ich długość może przekraczać 200 mm [4].

Przy takich proporcjach często miarodajną formą zniszczenia łącznika jest zginanie trzpienia, niewystępujące w przypadku połączeń blach cienkich, w których zastosowano wkręty krótkie, o kilku- lub kilkunastomilimetrowej długości trzpienia.

Kolejną przyczyną pomijania współpracy płyt warstwowych z konstrukcją nośną jest niewielka, znacznie niższa niż w przypadku pokryciowych blach trapezowych, grubość blach okładzinowych, wynosząca zazwyczaj 0,4–0,7 mm.

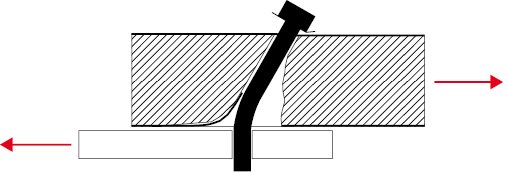
Efektem tego jest występowanie, przy stosunkowo niewielkich obciążeniach trwałych, plastycznych odkształceń blach okładzin w postaci owalizacji otworów [5] (RYS. 2, FOT. 1–2).

Próby modelowania zachowania się połączeń płyt warstwowych z konstrukcją nośną napotykały na dodatkowe trudności związane z wpływem temperatury i odkształceń reologicznych na mechaniczne właściwości syntetycznego rdzenia płyty.

W ciągu ostatnich 10 lat opracowano dwie metody obliczeniowe, przedstawione w pracy doktorskiej Markusa Dürra [6] oraz w wytycznych ECCS/CIB [7], które umożliwiają analityczną ocenę wpływu współpracy płyt warstwowych ze stalową konstrukcją wsporczą.

W przypadku obu metod jest to jednak możliwe jedynie w klasie konstrukcyjnej II (w rozumieniu normy PN-EN 1993-1-3:2008 [2]) oraz tylko przy statycznym i quasi-statycznym charakterze działających obciążeń.

Wpływ współpracy płyty z konstrukcją ogranicza się zatem jedynie do pojedynczych elementów, które mogą być dzięki temu zabezpieczone przed wystąpieniem zarówno giętnych, jak i giętno-skrętnych form niestateczności ogólnej.

Szczególnie istotne znaczenie ma to w przypadku projektowania elementów nośnych z zimnogiętych profili o kształcie zetowym i ceowym, które w normalnych warunkach podparcia i obciążenia są elementami zginanymi i skręcanymi.

Nie dopuszcza się uwzględniania współpracy płyt w analizie układów konstrukcyjnych, jakkolwiek możliwe jest wykorzystanie płyt warstwowych jako głównych elementów nośnych niewielkich obiektów, typu kioski handlowe, budynki gospodarcze itp.

Przytoczone opracowanie ECCS/CIB [7] ma jedynie rangę zaleceń, rozszerzających zakres stosowalności norm PN-EN 1993-1­‑3:2008 [2] i PN-EN 14509:2013-12 [8].

Zgodnie z p.10.1.1 (6) normy PN-EN 1993-1-3:2008 [2] elementy konstrukcyjne mogą być bowiem stężane poszyciem innym niż blacha trapezowa pod warunkiem odpowiedniego zaprojektowania połączeń tego poszycia z elementami podpierającymi.

W opracowywanych przez krajowy Instytut Techniki Budowlanej aprobatach technicznych nie poruszono kwestii współpracy płyt warstwowych z konstrukcją wsporczą.

W Niemczech Deutsches Institut für Bautechnik (DIBt) wydaje 2 rodzaje aprobat: dla płyt warstwowych samonośnych (selbsttragende Sandwich-Elemente), których wykorzystanie do stężania elementów konstrukcyjnych nie jest dozwolone, oraz nośnych płyt warstwowych (tragende Sandwich-Elemente), które można wykorzystywać do stężania elementów konstrukcyjnych; przy czym elementy te nie mogą stanowić stężeń innych elementów i ustrojów konstrukcyjnych obiektów budowlanych.

Aprobaty DIBt oraz zapisy w Załączniku Krajowym DIN EN 1993-1-3/NA (rozdz. NA 2.2) [9] umożliwiają stosowanie płyt warstwowych jako stężenia elementów konstrukcji stalowych w Niemczech [10].

Stężenia ciągłe elementów konstrukcji metalowych

W stalowych prętowych układach konstrukcyjnych element zginany lub ściskany rzadko występuje jako element pojedynczy.

Zwykle na jego długości projektowane są połączenia z innymi elementami nośnymi układu grawitacyjnego lub stężającego lub elementami uważanymi za niekonstrukcyjne - najczęściej stanowiącymi przegrodę budowlaną.

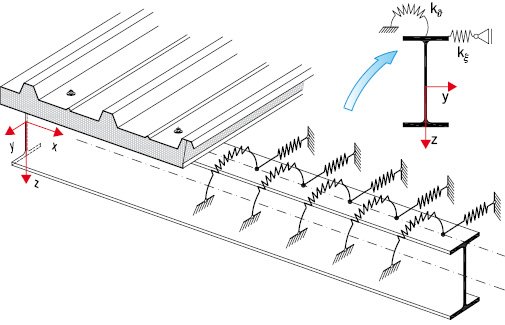
Poszycie w postaci blachy trapezowej lub płyt warstwowych z prawidłowo zaprojektowanymi i wykonanymi połączeniami może stanowić, ciągłe na długości pręta, odkształcalne więzi kinematyczne ograniczające zarówno przemieszczenia prostopadłe do osi pręta ξ, jak i obroty wokół jego osi ϑ (RYS. 3).

Więzi te charakteryzowane są przez sztywność translacyjną k_ξ i rotacyjną k_ϑ.

Niezwykle istotnym efektem redukcji przemieszczeń ξ i ϑ jest zwiększenie sił i momentów krytycznych elementów wsporczych, co może skutkować redukcją lub całkowitą eliminacją efektów niestateczności ogólnej elementu, przekładającą się bezpośrednio na zwiększenie nośności elementów ściskanych i zginanych.

Biorąc pod uwagę wartość oddziaływania więzi k₀ i k_ϑ na element prętowy, można mówić o stężeniu pełnym - gdy sztywność więzi jest na tyle duża, że o nośności elementu decyduje nośność przekrojowa, a współczynniki niestateczności ogólnej χ i lub χ LT można przyjmować równe 1,0, oraz o stężeniu częściowym - gdy współczynniki χ _i i χ _cLT przyjmują wartości mniejsze niż 1,0, jednak nadal są to wartości większe niż w przypadku elementu pozbawionego stężeń.

W tym ostatnim przypadku korzystny efekt stężenia za pomocą pokrycia można uwzględnić przez odpowiednie zwiększenie wartości N_cr i M_cr.

W przypadku więzi translacyjnej, oprócz wartości sztywności k_ξ, znaczenie ma również usytuowanie tej więzi na wysokości profilu względem skrajnych włókien ściskanych.

Jak wykazano m.in. w pracy V. Březiny [11], idealnie sztywna ciągła więź translacyjna, którą można uważać za wymuszoną oś obrotu przekroju,może stanowić stężenie pełne obciążonej równomiernie belki wolnopodpartej, pod warunkiem, że będzie usytuowana na wysokości nie mniejszej niż 46,6% wysokości strefy ściskanej.

Im bardziej więź ta będzie odsunięta od skrajnych włókien ściskanych, tym mniejszy będzie efekt stabilizacji.

W przypadku usytuowania stężenia na wysokości pasa rozciąganego niewielki pozytywny wpływ działania stężenia można całkowicie pominąć w uproszczonych obliczeniach inżynierskich, z korzyścią dla bezpieczeństwa konstrukcji.

Więzi ciągłe o sztywnościach k_ξ i k_ϑ odwzorowują stosunkowo złożony, nieliniowy charakter rzeczywistej współpracy mechanicznej poszycia z elementem podpierającym, w obowiązującej normie projektowania konstrukcji cienkościennych PN-EN 1993-1-3:2008 [2] więzi te oznaczono symbolami S_id i C_D.

Stężenie tworzące więź translacyjną jest najczęściej ukształtowane w postaci pasma blachy trapezowej albo pasma płyt warstwowych, usytuowanego między sąsiednimi zginanymi lub ściskanymi elementami konstrukcyjnymi obarczonymi wstępnymi imperfekcjami łukowymi.

O odkształcalności tej więzi w główniej mierze decyduje zatem nie sztywność podłużna poszycia, lecz jego sztywność postaciowa S oraz odkształcalność połączeń między poszyciem a elementem nośnym i między sąsiednimi arkuszami (płytami) poszycia.

Tworzone przez poszycie więzi translacyjne i rotacyjne współdziałają ze sobą i stabilizują element wsporczy.

Jeżeli poszycie jest zamocowane do pasa ściskanego, to w zależności od wartości sztywności postaciowej S można oczekiwać dwojakiego rodzaju współpracy wymienionych więzi.

Gdy sztywność postaciowa S jest wystarczająca do zapewnienia pełnego stężenia elementu wsporczego i odwzorowuje w modelu wymuszoną oś obrotu, to przemieszczenia rotacyjne nie wystąpią i sztywność rotacyjna k_ϑ nie zostanie „aktywowana”.

Jeśli sztywność postaciowa S nie wystarcza do uzyskania pełnego stężenia elementu podpierającego, mogą się pojawić deformacje skrętne i sztywność rotacyjna k_ϑ „aktywuje się” i stabilizuje dodatkowo element podpierający.

Uzyskanie pełnego stężenia elementu podpierającego poszycie jest możliwe zarówno przez spełnienie warunku minimalnej sztywności postaciowej:

S > S_min  (1)

jak i warunku minimalnej sztywności rotacyjnej:

(2)

Formuły pozwalające na określenie wartości minimalnych sztywności Smin i Cϑ, k,min podano w załączniku BB.2 normy PN-EN1993-1-1:2006/A1:2014-07 [12]:

gdzie:

E, G – odpowiednio moduł sprężystości i moduł sprężystości przy ścinaniu,

Iw – wycinkowy moment bezwładności profilu stężanego poszyciem,

IT – moment bezwładności przy skręcaniu swobodnym,

Iz – moment bezwładności względem osi „słabej”,

L – rozpiętość belki stężanej,

h – wysokość belki stężanej,

oraz:

(4)

gdzie:

M_{pl, k} – wartość charakterystyczna nośności plastycznej przekroju belki przy zginaniu,

E_Iz – sztywność giętna w płaszczyźnie osi „słabej” przekroju,

K_ν – współczynnik zależny od rodzaju analizy: 0,35 w przypadku analizy sprężystej oraz 1,0 w przypadku analizy plastycznej,

K_ϑ – współczynnik zależny od rozkładu momentów zginających i podparcia bocznego pasa ściskanego (TABELA 1).

Wartości współczynnika K_ϑ z TABELI 1 odpowiadające pasowi ściskanemu zamocowanemu nieprzesuwnie można przyjmować do obliczeń wtedy, gdy spełniony zostanie warunek (3).

Sztywność więzi rotacyjnej C_ϑ,k

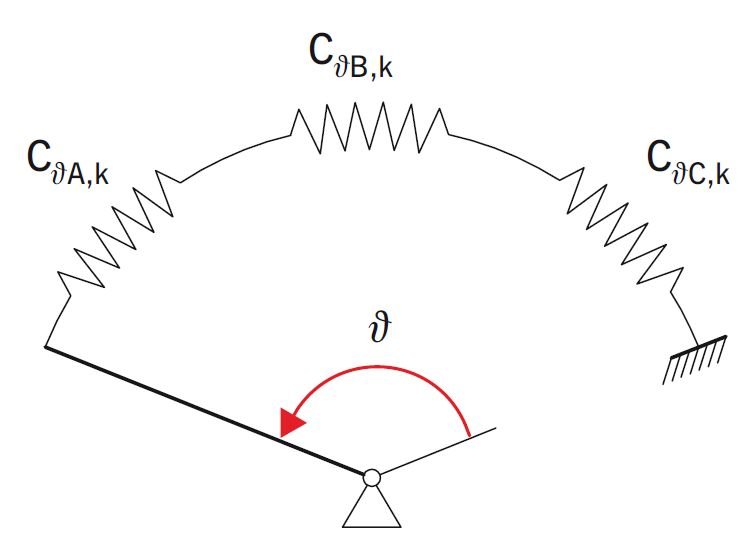
Model mechaniczny więzi rotacyjnej C_ϑ,k przedstawiany jest najczęściej jako układ trzech szeregowo połączonych sprężyn rotacyjnych (RYS. 4) związanych zależnością:

(5)

C_ϑA,k – sztywność sprężyny rotacyjnej reprezentującej wpływ sztywność połączenia panel - kształtownik,

C_ϑB,k – sztywność sprężyny rotacyjnej reprezentującej sztywność dystorsyjną kształtownika,

C_ϑC,k – sztywność sprężyny rotacyjnej reprezentującej sztywność giętną płyty warstwowej w płaszczyźnie prostopadłej do osi elementu podpierającego.

Składnik C_ϑB,k występujący w (5) wprowadzono ze względu na to, że w rzeczywistym połączeniu poszycia z kształtownikiem więź rotacyjna usytuowana jest na powierzchni jednego z pasów profilu, a nie w jego osi, stąd odkształcenia dystorsyjne nie mogą być pominięte [13].

Uszeregowanie składników sztywności względem indeksów dolnych (A, B, C), analogicznie jak w normie PN-EN 1993-1-3:2008 [2], nie jest przypadkowe - odpowiada stopniowi wpływu danej wielkości na całkowitą sztywność obrotową C_ϑ,k.

Największą liczbowo wartość stanowi sztywność C_ϑC,k, często pomijana w obliczeniach uproszczonych. Wielkość ta może być wyznaczona analitycznie.

Jest uzależniona od sztywności giętnej panelu i schematu statycznego poszycia, w tym liczby przęseł. Sztywność C_ϑC,k, zgodnie z normą PN-EN 1993-1-3:2008 [2], można wyznaczyć za pomocą formuły:

(6)

gdzie:

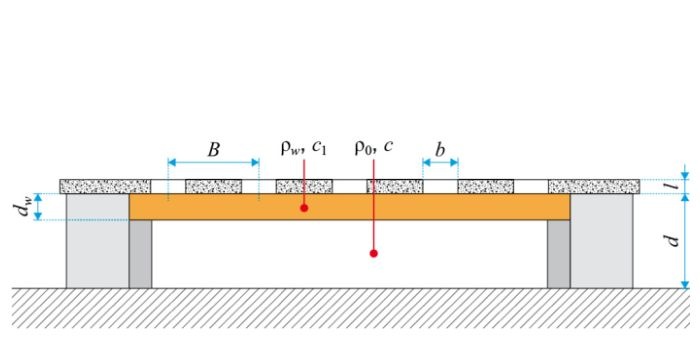
m_ϑ – moment zginający poszycie przypadający na jednostkę długości płatwi (RYS. 5–6), [kNm/m],

ϑ – kąt obrotu płatwi (równy kątowi obrotu przekroju podporowego poszycia), [rad].

Alternatywnie dopuszcza się wyznaczanie sztywności C_ϑC,k w sposób przybliżony [2]:

(7)

gdzie:

k – współczynnik liczbowy zależny od podatności poszycia oraz umiejscowienia płatwi i konfiguracji obrotów płatwi sąsiednich, zdefiniowany na RYS. 5–6,

E – moduł sprężystości,

I_eff – moment bezwładności przekroju przypadający na jednostkę szerokości poszycia,

s – osiowy rozstaw płatwi.

Sztywność C_ϑB,k, związana z dystorsją profilu płatwi, jest funkcją geometrii i właściwości materiałowych płatwi, kierunku obciążenia oraz usytuowania łączników na pasie i może być wyznaczona analitycznie [14]:

(8)

gdzie:

ν – współczynnik Poissona,

h – wysokość profilu mierzona w osiach środkowych ścianek,

t_w – grubość ścianki środnika,

t_f – grubość ścianki pasa,

c₁ – współczynnik zależny od rodzaju przekroju i znaku obciążenia (dociskające, unoszące):

W przypadku gdy pas ściskany przekroju jest stężony lub odkształcenia dystorsyjne przekroju są pomijalnie małe (np. dla profili gorącowalcowanych), zgodnie z zapisem normy PN-EN 1993-1­‑1:2006/A1:2014-07 [12] można przyjmować C_ϑB,k = ∞.

Rotacyjna sztywność połączenia płyty warstwowej z płatwią C_ϑA,k nie została podana w normach PN-EN 1993-1-3:2008 [2], PN-EN 1993-1-1:2006/A1:2014-07 [12].

Do niedawna można ją było wyznaczać jednie na drodze doświadczalnej.

Obecnie opracowane są dwie metody analitycznego wyznaczania wartości C_?A,k.

Przedstawiono je w wytycznych ECCS/CIB [7] oraz w pracy doktorskiej Dürra [6], która stała się podstawą do utworzenia odpowiednich zapisów normy DIN 18800-2:2008 [15] oraz niemieckiego Załącznika Krajowego do normy DIN-EN 1993-1-3 [10].

Ze względu na szerszy zakres stosowalności (TABELA 2) przedstawiono metodę podaną w wytycznych ECCS/CIB [7].

Sztywność połączenia płyty warstwowej z płatwią C_ϑA,k jest funkcją: szerokości pasa płatwi, liczby i położenia wkrętów na pasie, sztywności giętnej okładziny płyty przylegającej do pasa oraz sztywności na ściskanie rdzenia płyty.

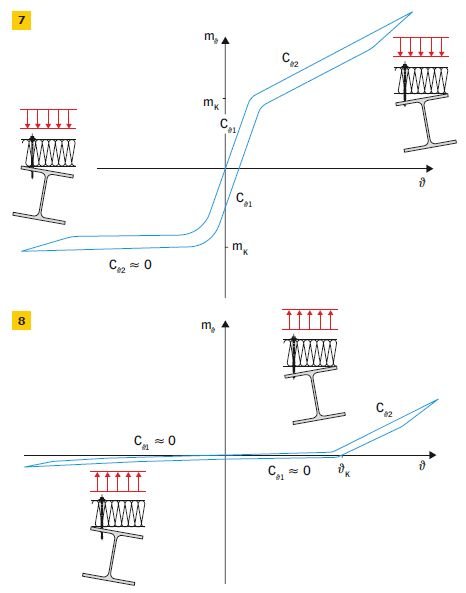
Na podstawie otrzymanych na drodze eksperymentalnej [7] charakterystyk sztywności połączenia płatew – płyta warstwowa, wykonanych dla przypadku obciążenia dociskającego (RYS. 7) oraz obciążenia unoszącego (RYS. 8), można zauważyć, że znak obciążenia w istotny sposób wpływa na sztywność połączenia.

W obydwu wymienionych przypadkach badania wykonano w pełnym cyklu obciążeniowym (0, +m_ϑmax, −m_ϑmin, 0), co pozwoliło na pomiar odkształceń trwałych oraz ujawniło pętlę histerezy, której powierzchnia może być traktowana jako miara energii rozproszonej w połączeniu.

Charakterystyki empiryczne w zakresie ścieżki obciążeniowej można opisać zależnością biliniową opisaną dwoma parametrami C_ϑ1 i C_ϑ2 z punktem przejścia o współrzędnych m_K, q_K.

Punkt przejścia odpowiada wartości momentu skręcającego m_K, przy której w trzpieniu łącznika zaczyna działać siła rozciągająca, tworząca wraz z siłą docisku na krawędzi pasa parę sił umożliwiającą przekazywanie momentu skręcającego między pławią a płytą warstwową.

Moment skręcający m_K określany jest w literaturze jako moment kontaktu.

Jeśli porówna się charakterystyki przedstawione na RYS. 7 i RYS. 8, można zauważyć, że w przypadku działania obciążeń unoszących (RYS. 8) sztywność obrotowa połączenia w zakresie kątów obrotu (0, m_K) jest pomijalnie mała, zarówno dla dodatnich, jak i ujemnych wartości kątów obrotu ϑ.

Płyta warstwowa nie może być zatem stosowana jako zabezpieczenie płatwi przed zwichrzeniem w przypadku działania obciążeń unoszących.

Więź rotacyjna może być efektywna i zwiększać nośność płatwi na zwichrzenie jedynie w przypadku działania obciążeń dociskających.

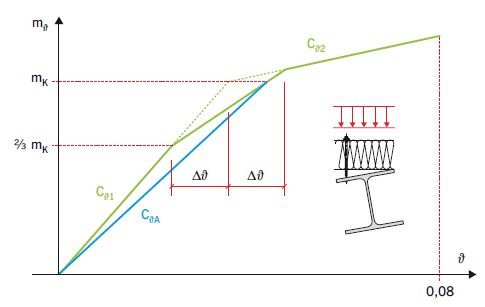
Na RYS. 9 pokazano obliczeniową trójliniową charakterystykę połączenia belka–płyta warstwowa, którą można wykorzystywać w komputerowym modelowaniu współpracy belek z pokryciem z płyt warstwowych.

W przypadku ręcznego prowadzenia obliczeń uproszczonych korzystniejsze jest posłużenie się aproksymacją sieczną charakterystyki obliczeniowej, której konstrukcję geometryczną pokazano na RYS. 9.

Stosowanie charakterystyki siecznej ograniczone jest do wartości momentu skręcającego m_K, będącego funkcją obliczeniowej wartości obciążenia dociskającego q_d:

(9)

Rotacyjną sztywność połączenia CϑA można zatem wyznaczyć z zależności (RYS. 9):

(10)

Wartości sztywności C_ϑ1 i C_ϑ2 uzależnione są od modułu sprężystości rdzenia płyty, który jest funkcją rodzaju materiału rdzenia, czasu działania obciążenia oraz temperatury eksploatacyjnej:

(11)

gdzie:

E_C – wartość średnia modułu sprężystości rdzenia przy ściskaniu E_Cc i rozciąganiu E_Ct,

φ_ϑ,t – współczynnik pełzania, zależny od czasu t ekspozycji na obciążenie wyrażonego w godz.:

φ_ϑ,2000 = 1,29 dla rdzeni PU i EPS,

φ_ϑ,2000 = 1,35 dla rdzeni MWF,

φ_ϑ,100000 = 1,83 dla rdzeni PU i EPS,

φ_ϑ,100000 = 2,31 dla rdzeni MWF,

k₁ – współczynnik wpływu temperatury na moduł sprężystości rdzenia przy rozciąganiu według normy PN-EN 14509:2013-12 [8]:

(12)

gdzie:

E_Ct,+20°C, E_Ct,+80°C – moduł sprężystości rdzenia przy rozciąganiu wyznaczony w temp. +20°C i +80°C.

Należy zwrócić uwagę, że sztywności C_ϑ1 i C_ϑ2 oraz moment kontaktu m_K wyznacza się odmiennie dla przekrojów walcowanych na gorąco i profilowanych na zimno (TABELA 3).

c₁, c₂, c₃ – parametry przyjmowane według TABELI 4,

b – szerokość pasa belki, [mm],

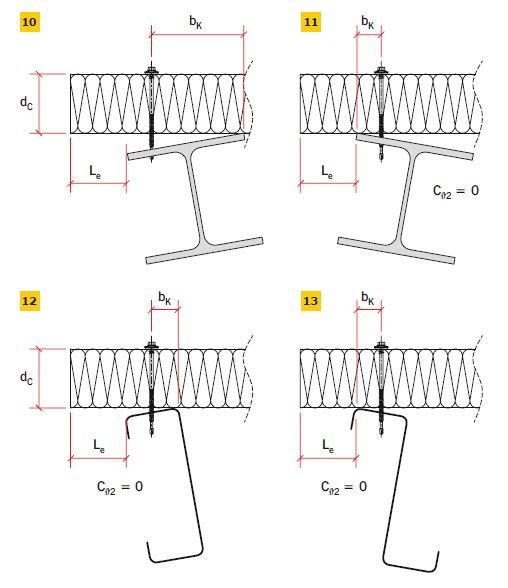
b_K – odległość między linią łączników a linią docisku pasa belki do płyty warstwowej (RYS. 10–13), [mm],

n_f – liczba łączników na 1 m długości linii łączników, (n_f = 0 w przypadku łączników ukrytych w zamku płyt oraz gdy b_K < 0,5b), [1/m],

q – obciążenie dociskające przekazywane z panelu na belkę, [kN/m].

Płyta jest uważana za profilowaną, jeśli wysokość fałd ≥ 30 mm.

Stany graniczne połączenia płyty warstwowej z konstrukcją nośną

W przypadku stosowania uproszczonej metody obliczeniowej wykorzystującej sieczną wartość sztywności rotacyjnej CϑA destabilizujący moment skręcający mϑA, wywoływany drugorzędnym skręcaniem belki, można wyznaczyć za pomocą formuły [16]:

(13)

gdzie:

ϑ₀ – amplituda skręcenia wstępnego belki, ϑ₀ = 0,06 rad,

k_c – współczynnik poprawkowy zależny od rozkładu momentu zginającego na długości weryfikowanego elementu według tabl. 6.6 normy PN-EN 1993-1-1:2006/A1:2014-07 [12],

M_Ed – wartość obliczeniowa maksymalnego momentu zginającego w płaszczyźnie osi słabej profilu,

I_z – moment bezwładności profilu względem osi słabej.

W przypadku stosowania uproszczonej metody obliczeniowej wartość maksymalnego momentu skręcającego m_ϑA nie może przekraczać wartości obliczeniowej momentu kontaktu m_K:

(14)

Również kąty obrotu belki ϑ w przypadku stosowania metody uproszczonej muszą spełniać warunek:

(15)

gdzie:

m_K,k – moment kontaktu wyznaczony na podstawie kombinacji obciążeń stanu granicznego użytkowalności.

Ograniczenie kątów skręcenia przekroju do wartości 0,08 rad zapewnia ograniczenie odkształceń plastycznych okładziny w miejscu docisku łba oraz deformacji metalowej podkładki i uszczelki z tworzywa sztucznego.

Jak doświadczalnie wykazano w pracy doktorskiej Markusa Dürra [6], pozwala to na utrzymanie wodoszczelności połączenia przy działaniu ciśnienia 10 cm słupa wody przez 24 godz.

W przypadku wykorzystywania metod przyrostowej analizy nieliniowej oraz trójliniowej charakterystyki m_ϑ–ϑ, moment skręcający m_ϑ nie musi być już ograniczany do wartości momentu kontaktu m_K.

Obowiązują jednak nadal ograniczenia maksymalnych kątów skręcenia ϑ. Należy także kontrolować wartości sił w łącznikach.

Siły te można wyznaczać według tabl. 10.4 normy PN-EN 1993­‑1-3:2008 [2], przy czym w obliczeniach należy uwzględniać dodatkowe siły rozciągające łączniki n_Ed, wynikające ze stabilizacyjnego działania poszycia z płyt warstwowych:

gdzie:

n_fst – liczba łączników przypadająca na 1 m belki.

Przykład obliczeniowy

Sprawdzono możliwość wykorzystania płyt warstwowych do stężenia 6-przęsłowej ciągłej płatwi dachowej. Do obliczeń przyjęto następujące dane:

• rozpiętość przęsła płatwi l_b = 6,0 m,
• liczba przęseł płatwi n_p = 6,
• profil płatwi – IPE180,

– wysokość profilu h = 180 mm,

– szerokość półki b = 91 mm,

moment bezwładności względem osi „słabej” I_z = 101 cm⁴,

• materiał płatwi – stal S235 o module sprężystości E = 210 GPa,
• płyta warstwowa:

– szerokość modularna płyty bp = 1200 mm,

– materiał rdzenia – pianka poliuretanowa (PUR),

– moduł sprężystości rdzenia przy ściskaniu ECc = 4,0 N/mm2,

– moduł sprężystości rdzenia przy rozciąganiu (θ = +20°C) ECt+20 = 3,0 N/mm2,

– moduł sprężystości rdzenia przy rozciąganiu (θ = +80°C) ECt+80 = 2,6 N/mm2,

– wytrzymałość rdzenia na ściskanie fCc = 0,12 N/mm2,

– wytrzymałość rdzenia na rozciąganie fCt = 0,20 N/mm2,

– współczynnik czasu trwania obciążenia φθ,2000 = 1,29,

– materiał okładzin – stal S280GD

– grubość okładziny zewnętrznej text = 0,55 mm,

– grubość okładziny wewnętrznej tint = 0,40 mm,

• łączniki płyty warstwowej – wkręty samowiercące φ 6,3/5,5×200

– liczba wkrętów przypadająca na 1 płytę nw = 3,

– liczba wkrętów przypadająca na 1,0 m płyty nf = nw/bp = 2,5 m–1,

– średnica podkładki dw = 19 mm,

– odległość łączników od krawędzi pasa bk = 0,75b = 68 mm,

• obciążenia płatwi

– obciążenie stałe (wartość charakterystyczna) qGk = 0,5 kN/m,

– obciążenie zmienne (wartość charakterystyczna) qQk = 1,80 kN/m,

– sumaryczna wartość obciążenia charakterystycznego qk = 2,30 kN/m,

– sumaryczna wartość obciążenia obliczeniowego qd = qGk 1,35 + qQk 1,50 = 3,38 kN/m,

Sprawdzenie warunków stosowalności metody obliczeniowej:

b = 91 mm = b_min = 91 mm,

E_{Cc, min} = 2,0 N/mm² < E_Cc = 4,0 N/mm² < E_{Cc, max} = 8,0 N/mm²,

t_{cor, min} = 0,38 mm < t_ext = 0,55 mm < t_{cor, max} = 0,71 mm,

t_{cor, min} = 0,38 mm < t_int = 0,40 mm < t_{cor, max} = 0,71 mm,

>n_{f, min} = 1,0 m^-1 < n_f = 2,5 m^-1 < n_{f, max} = 4,0 m^–1,

f_Cc = 0,12 N/mm² > f_Cc = 0,08 N/mm²,

f_Ct = 0,20 N/mm² > f_Ct = 0,06 N/mm²,

d_w = 19 mm > d_{w, min} = 16 mm

Warunki stosowalności metody zostały spełnione.

• wartość średnia modułu sprężystości rdzenia przy ściskaniu i rozciąganiu w temp. 20°C:

E_C = 0,5 (E_Cc + E_Ct) = 3,5 N/mm²,

• współczynnik wpływu temperatury:
• 
• zredukowany moduł sprężystości rdzenia:
•  N/mm²

Na podstawie TABELI 4 odpowiednio do materiału rdzenia przyjęto wartości współczynników pomocniczych jak dla płyty profilowanej: c1 = 0,18 i c2 = 0,052 m,

• sztywności charakterystyki m>_ϑϑ połączenia pokrycia z płatwią:

Cϑ1 = c1·ECtθ·b2 = 2,278 kNm/m,

Cϑ2 = c2· nf ·ECtθ·bK2 = 0,926 kNm/m,

• sztywność sieczna:

 kNm/m,

• moment kontaktu w stanie granicznym nośności:

mK = qdb/2 = 0,154 kNm/m

• maksymalny moment zginający płatew (przyjęto moment sprężysty, ze względu na niewielki stopień wytężenia):

MEd = 0,105qdlb2 = 0,157 kNm/m

• współczynnik korekcyjny uwzględniający rozkład momentów zginających na długości przęsła płatwi według tabl. 6.6 normy PN-EN 1993-1-1:2006/A1:2014-07 [12]:

kc = 0,91

• kąt wstępnego skręcenia płatwi:

ϑ0 = 0,06 rad

• moment skręcający stabilizujący płatew:

 kNm/m

Sprawdzenie warunku stanu granicznego nośności połączenia płatwi z płytą warstwową:

mϑA = 0,153 kNm/m < mK = 0,154 kNm/m

Warunek stabilizacji płatwi został spełniony.

Dodatkowo należy sprawdzić nośność łączników na działanie sił rozciągających nEd wynikających z działania momentu mϑA.

Moment kontaktu w stanie granicznym użytkowalności:

mK,k = qk·b/2 = 0,105 kNm/m

Kąt skręcenia płatwi wywołany działaniem momentu mK,k:

ϑEk = mK,k/CϑA = 0,052 rad

Sprawdzenie warunku stanu granicznego użytkowalności połączenia płatwi z płytą warstwową:

ϑEk = 0,052 rad < ϑlim = 0,080 rad

Warunek został spełniony.

Podsumowanie

Współpraca płyt warstwowych ze stalowym szkieletem nośnym była dotychczas pomijana w obliczeniach statyczno-wytrzymałościowych ze względu na trudności w modelowaniu połączenia płyty z elementem nośnym konstrukcji.

W ostatnich latach opracowano metody pozwalające uwzględnić współpracę płyty warstwowej z elementami nośnymi, m.in. w pracy doktorskiej Markusa Dürra [6] oraz w wytycznych ECCS/CIB [7].

Metody te oparte są na wynikach badań doświadczalnych, w związku z tym ich stosowalność jest ograniczona parametrami: obciążenia, łączników, geometrii kształtownika i płyty warstwowej oraz materiału rdzenia płyty.

Podczas obliczeń należy zwrócić uwagę na to, że możliwość stężania konstrukcji nośnej nie jest permanentną cechą płyt warstwowych, lecz stanowi funkcję obciążenia i wymaga weryfikacji zarówno na poziomie stanu granicznego nośności, jak i użytkowalności.

Literatura

1. T. Markiton, „40 lat płyt warstwowych w Polsce (1974–2014)”, „Nowoczesne Hale”, nr 3/2014.
2. PN-EN 1993-1-3:2008, „Eurokod 3: Projektowanie konstrukcji stalowych. Część 1-3. Reguły ogólne. Reguły uzupełniające dla konstrukcji z kształtowników i blach profilowanych na zimno”.
3. PN-EN 1990:2004, „Eurokod. Podstawy projektowania konstrukcji”.
4. B. Gosowski, E. Kubica, „Badania laboratoryjne konstrukcji metalowych”, Oficyna Wydawnicza Politechniki Wrocławskiej, Wrocław 2012.
5. J. Mareš, F. Wald, Z. Sokol, „Modelling of Joints of Sandwiches Panels, The Paramount Role of Joints into the Reliable Response of Structures”, NATO Science Series, vol. 4/2000, s. 387–394.
6. M. Dürr, „Die Stabilisierung biegedrillknickgefährdeter Träger durch Sandwichelemente und Trapezbleche” [praca doktorska], Universität Federiciana zu Karlsruhe, Karlsruhe 2008.
7. „European Recommendation on the Stabilization of Steel Structures by Sandwich Panels”, ECCS/CIB Joint Committee, 1st Edition, 2013.
8. PN-EN 14509:2013-12, „Samonośne izolacyjno-konstrukcyjne płyty warstwowe z dwustronną okładziną metalową. Wyroby fabryczne. Specyfikacje”.
9. DIN EN 1993­1­3:2010, „Eurocode 3: Bemessung und Konstruktion von Stahlbauten. Teil 1­3: Allgemeine Regeln – Ergänzende Regeln für kaltgeformte Bauteile und Bleche”.
10. S. Käpplein, K. Berner, T. Ummenhofer, „Stabilisierung von Bauteilen durch Sandwichelemente”, „Stahlbau”, vol. 81, 12/2012.
11. V. Březina, „Stateczność prętów konstrukcji metalowych”, Arkady, Warszawa 1966.
12. PN-EN 1993-1-1:2006/A1:2014-07, „Eurokod 3. Projektowanie konstrukcji stalowych. Część 1-1. Reguły ogólne i reguły dla budynków”.
13. J. Goczek, Ł. Supeł, „Płatwie z kształtowników profilowanych na zimno”, Wydawnictwo Politechniki Łódzkiej, Łódź 2014.
14. J. Lindner, J. Scheer, H. Schmidt, „Stahlbauten. Erläuterungen zu DIN 18800 Teil 1 bis Teil 4, 1”, Auflage, Beuth Verlag GmbH und Ernst & Sohn, Berlin-Köln 1993.
15. DIN 18800-2:2008, „Stahlbauten. Teil 2: Stabilitätsfälle. Knicken von Stäben und Stabwerken”.
16. J. Lindner, „Anschlußmomente von Trägern die zur Kippaussteifung herangezogen werden”, „Bautechnik”, vol. 50, 10/1973, s. 342–344.

Chcesz być na bieżąco? Zapisz się do naszego newslettera!