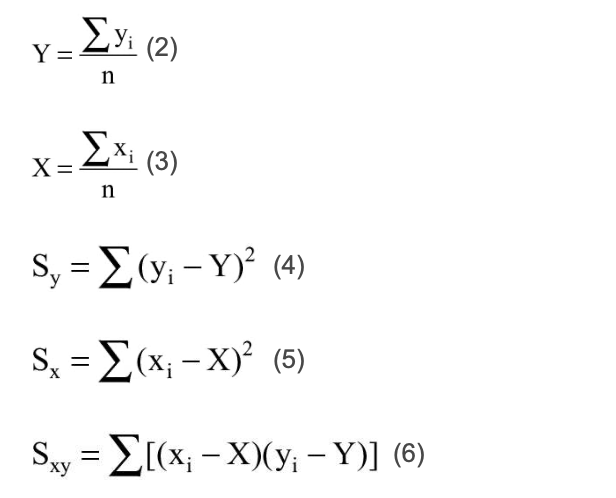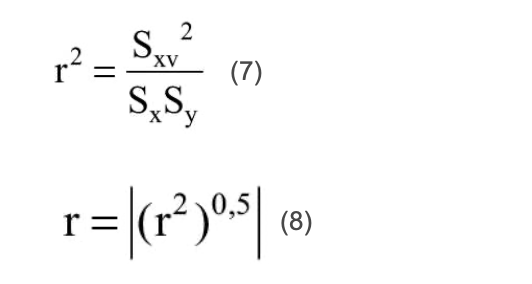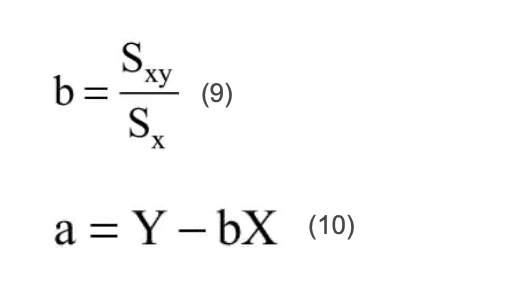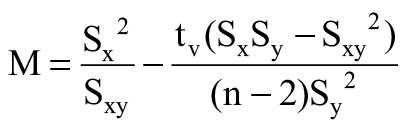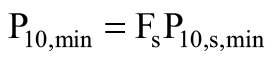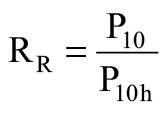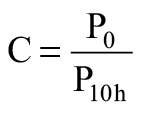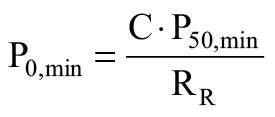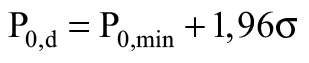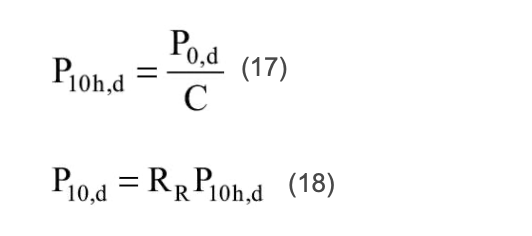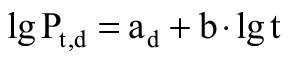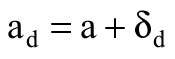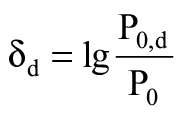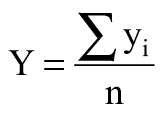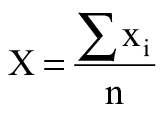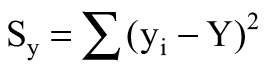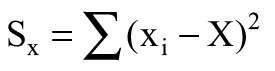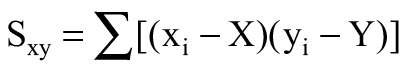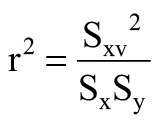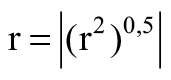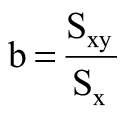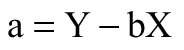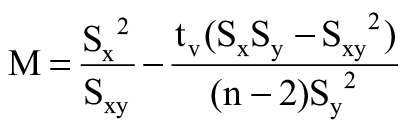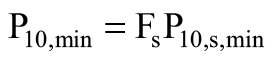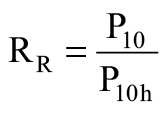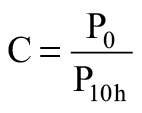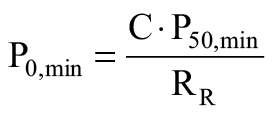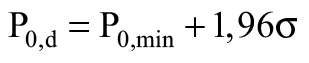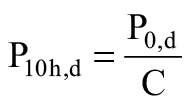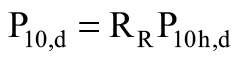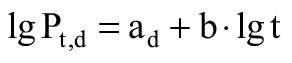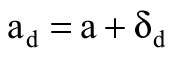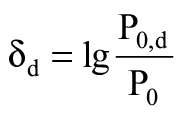Projektowanie systemów ociepleń w oparciu o badania starzeniowe
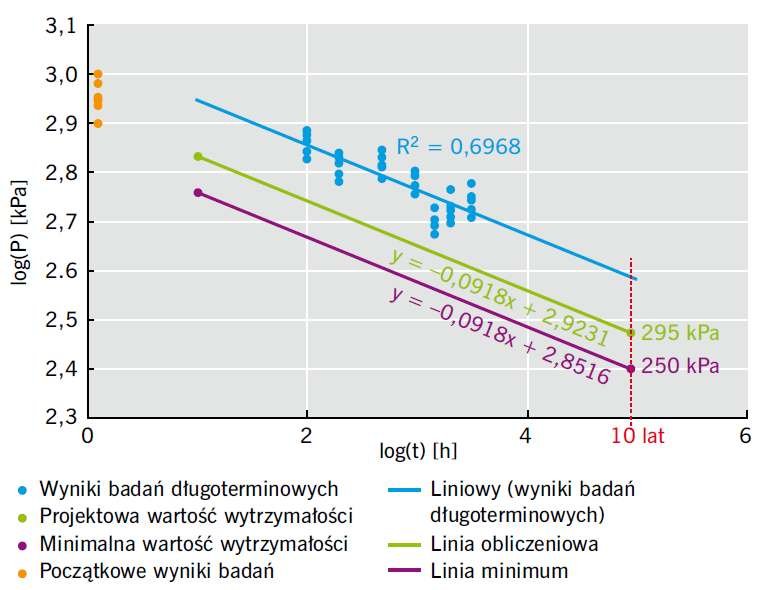
Ekstrapolacja danych na podstawie analizy regresji

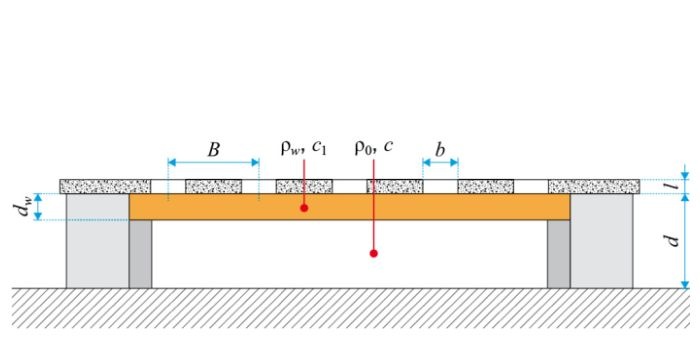
Układ warstw poddanych odrywaniu metodą pull-off
Archiwa autorów
Gwarancje udzielane przez producentów materiałów budowlanych powinny być poparte badaniami pozwalającymi określić, czy właściwości wyrobu nie zmienią się w zakresie zadeklarowanych wartości w czasie krótszym niż przewiduje okres gwarancji. W tym celu stosuje się długoterminowe badania starzeniowe.
Zobacz także
Fiberglass Fabrics sp. z o.o. Tynki i farby w dużych inwestycjach budowlanych

Przy projektowaniu i realizacji dużych inwestycji, takich jak osiedla mieszkaniowe, biurowce czy obiekty użyteczności publicznej, kluczowe znaczenie ma wybór odpowiednich materiałów wykończeniowych. Nie...
Przy projektowaniu i realizacji dużych inwestycji, takich jak osiedla mieszkaniowe, biurowce czy obiekty użyteczności publicznej, kluczowe znaczenie ma wybór odpowiednich materiałów wykończeniowych. Nie do przecenienia jest rola tynków i farb, które wpływają na wygląd budynków, a także na ich trwałość i komfort użytkowania.
Connector.pl Nowoczesne piany poliuretanowe – szczelne i trwałe ocieplenie budynku

Firma Connector.pl to największy polski dystrybutor materiałów do produkcji kompozytów, będący liderem na rynku od ponad 30 lat. W swojej ofercie posiadamy szeroką gamę produktów, a wśród nich znakomitej...
Firma Connector.pl to największy polski dystrybutor materiałów do produkcji kompozytów, będący liderem na rynku od ponad 30 lat. W swojej ofercie posiadamy szeroką gamę produktów, a wśród nich znakomitej jakości piany PUR otwarto- i zamkniętokomórkowe.
Czytaj całość »
M.B. Market Ltd. Sp. z o.o. Czy piana poliuretanowa jest palna?
W artykule chcielibyśmy przyjrzeć się bliżej temu aspektowi i rozwiać wszelkie wątpliwości na temat palności pian poliuretanowych.
W artykule chcielibyśmy przyjrzeć się bliżej temu aspektowi i rozwiać wszelkie wątpliwości na temat palności pian poliuretanowych.
Czytaj całość »Każdy materiał ulega starzeniu i jest to proces nieodwracalny. Projektowanie wyrobu powinno przebiegać w taki sposób, aby zastosowane surowce w jak największym stopniu ograniczały proces starzenia, którego naturalnym efektem jest zmiana właściwości wyrobu.
Odpowiednie zaplanowanie i przeprowadzenie badań starzeniowych oraz obróbka statystyczna wyników pozwalają określić parametry produktu czy kompozytu nawet po 50 latach użytkowania [1, 2].
Aby przyspieszyć proces starzenia, często korzysta się z tzw. komór klimatycznych, symulujących zmienne warunki atmosferyczne, w których produkt lub zestaw produktów mają być eksploatowane, a czas starzenia określają normy przedmiotowe. Podczas planowania i wykonywania badań starzeniowych istotne są:
- wybór odpowiednich właściwości badanych w próbach niszczących lub nieniszczących, których zmiany rejestrowane są w funkcji czasu,
- dobór odpowiednich cykli starzeniowych.
W artykule przedstawiono wyniki opracowane przy zastosowaniu nowatorskich dla ociepleń algorytmów, często stosowane w innych branżach przemysłu, które po odpowiednich modyfikacjach można stosować podczas projektowania produktów wchodzących w skład kompletnych systemów ociepleń.
Są one poparte obliczeniami statystycznymi potwierdzającymi przydatność danych do ekstrapolacji, a jednocześnie określenia wartości przyczepności międzywarstwowej po 10 latach użytkowania na bazie wartości początkowych oraz wyników badań starzeniowych.
Przedstawione badania na przykładzie jednego z systemów w sposób wyczerpujący opisują podejście do udzielania wydłużonej gwarancji na system ociepleń. Odpowiednia analiza obliczeniowa potwierdza natomiast poprawność stosowanej metody w określaniu właściwości po długim okresie użytkowania.
|
Należy podkreślić, że żadne normy ani wytyczne dla systemów ociepleń [3, 4] nie określają rzeczywistego czasu, jakiemu odpowiada starzenie wyrobu w symulowanych warunkach w laboratorium, a jedynie pozwalają określić pewne właściwości po starzeniu. Według wytycznych przewidywany okres trwałości ocieplenia to 25 lat, jednak obserwacje rynku systemów ociepleń tego nie potwierdzają. Często fasady budynków wymagają napraw już po kilku latach i znaczna część przypadków nie jest wynikiem błędów wykonawczych, lecz skutkiem zastosowania materiałów nieodpowiedniej jakości [5]. Zastosowanie opisanej w artykule metody pozwala na świadome udzielanie wydłużonej, 10-letniej gwarancji na kompletne systemy ociepleń. Ze względu na to, iż krytyczną cechą bezspoinowych systemów ociepleń jest przyczepność międzywarstwowa, właściwość ta została wybrana do długoterminowych badań starzeniowych jako najlepiej obrazująca proces starzenia. |
ABSTRAKT |
W artykule przedstawiono analizę regresji z ekstrapolacją jako narzędzie do przewidywania okresu trwałości lub zmiany parametru na bazie danych z badań starzeniowych oraz wytrzymałości początkowych. Podano wzory do obliczeń oraz uzyskane wyniki.Design of thermal insulation systems on the basis of aging tests. extrapolation of data on the basis of regression analysisThe article presents analysis of regression with extrapolation as a tool to anticipate the useful life or change of performance on the basis of data obtained through aging tests and initial resistance values. The computation formulas and results are presented. |
Przyczepność międzywarstwowa w rozumieniu przedstawionej metody to adhezja między poszczególnymi składnikami warstwy wierzchniej, tzn. klejem do warstwy zbrojącej, gruntem podtynkowym oraz wyprawą tynkarską.
Aby zapewnić możliwość oceny rzeczywistej przyczepności warstw zamiast wytrzymałości na rozrywania materiału izolacyjnego, próbki warstwy wierzchniej systemu przyklejono do podłożą betonowego. W dalszej części artykułu badany parametr będzie nazywany wytrzymałością (P), wyrażoną jako stosunek siły odrywającej do powierzchni odrywanej próbki.
Przebieg badania
Badanie przyczepności międzywarstwowej polega na wyznaczeniu siły odrywającej warstw wierzchnich systemu (warstwy zbrojonej siatką szklaną z gruntem podtynkowym i wyprawą tynkarską) po uprzednim usunięciu termoizolacji i przyklejeniu ich do płyty betonowej za pomocą np. kleju epoksydowego. Na FOT. przedstawiono układ warstw. Powierzchnia odrywanej próbki wynosi ok. 2500 mm².
Badania wykonano na próbkach sezonowanych 28 dni w laboratorium i niepoddanych starzeniu (wyniki początkowe) oraz po różnym okresie starzenia próbek w komorze klimatycznej według następujących cykli starzeniowych, symulujących zmienne warunki cieplno-wilgotnościowe:
- 10 cykli nagrzewanie - zraszanie (60 godz.):
- nagrzewanie do 70°C w ciągu 1 godz. i utrzymywanie temperatury przez 2 godz.,
- zraszanie wodą przez 1 godz.,
- pozostawienie na 2 godz., - 3 cykle nagrzewanie - oziębianie (36 godz.):
- nagrzewanie do 50°C w ciągu 1 godz. i utrzymywanie temperatury przez 3 godz.;
- spadek temperatury do -20°C w ciągu 2 godz. i utrzymywanie jej przez 6 godz.
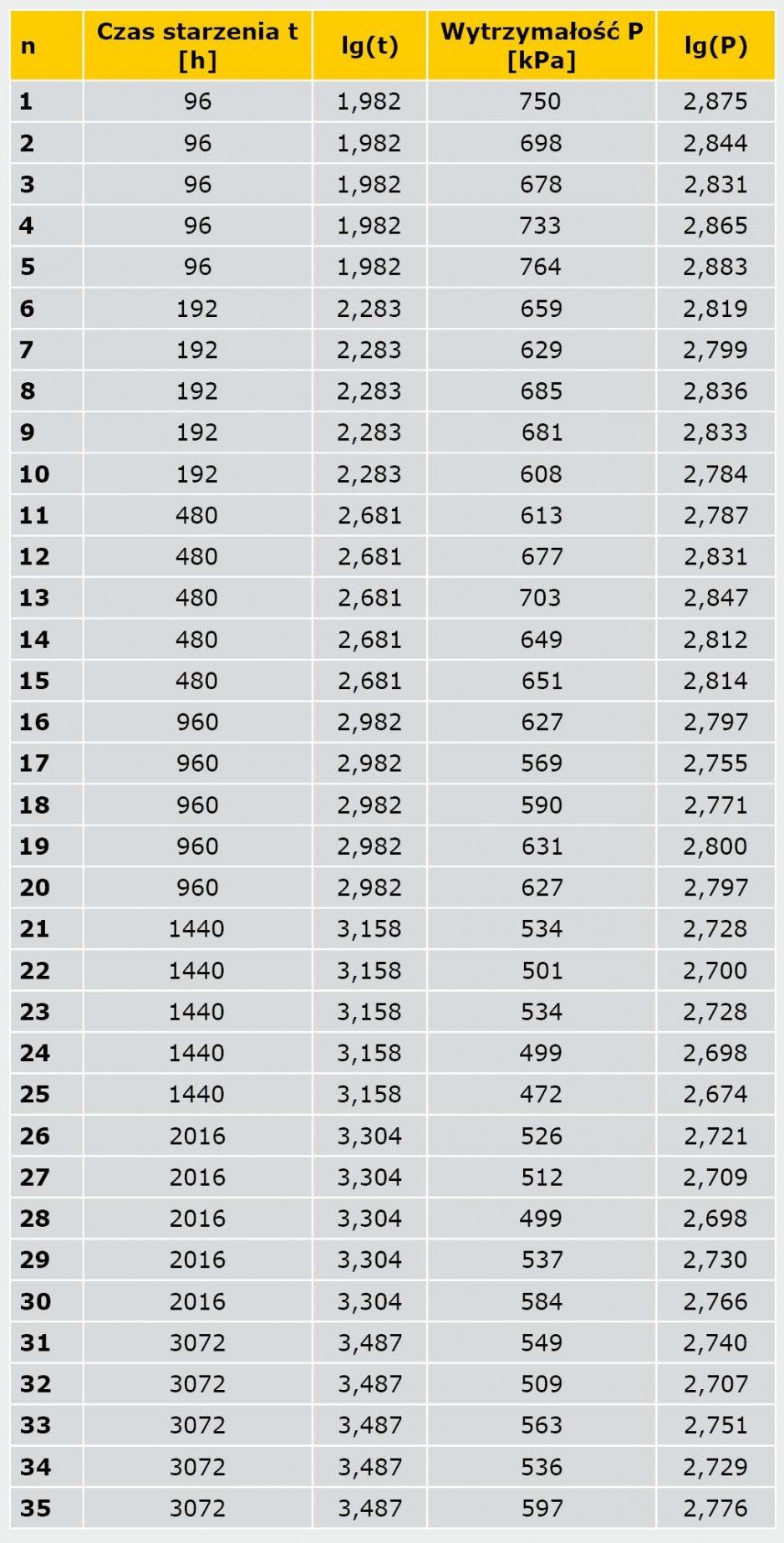
Po 96 godz. poddano badaniu 5 próbek. Kolejne próbki badano po 192 godz., 480 godz., 960 godz., 1440 godz., 2016 godz. oraz 3072 godz. starzenia.
Otrzymane wyniki po cyklach starzeniowych wykorzystano do obliczenia krzywej regresji, a następnie parametru projektowego wytrzymałości po 10 latach eksploatacji.
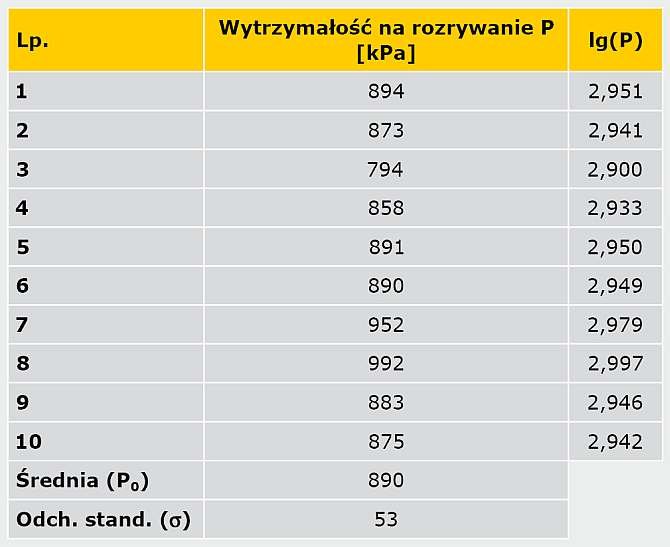
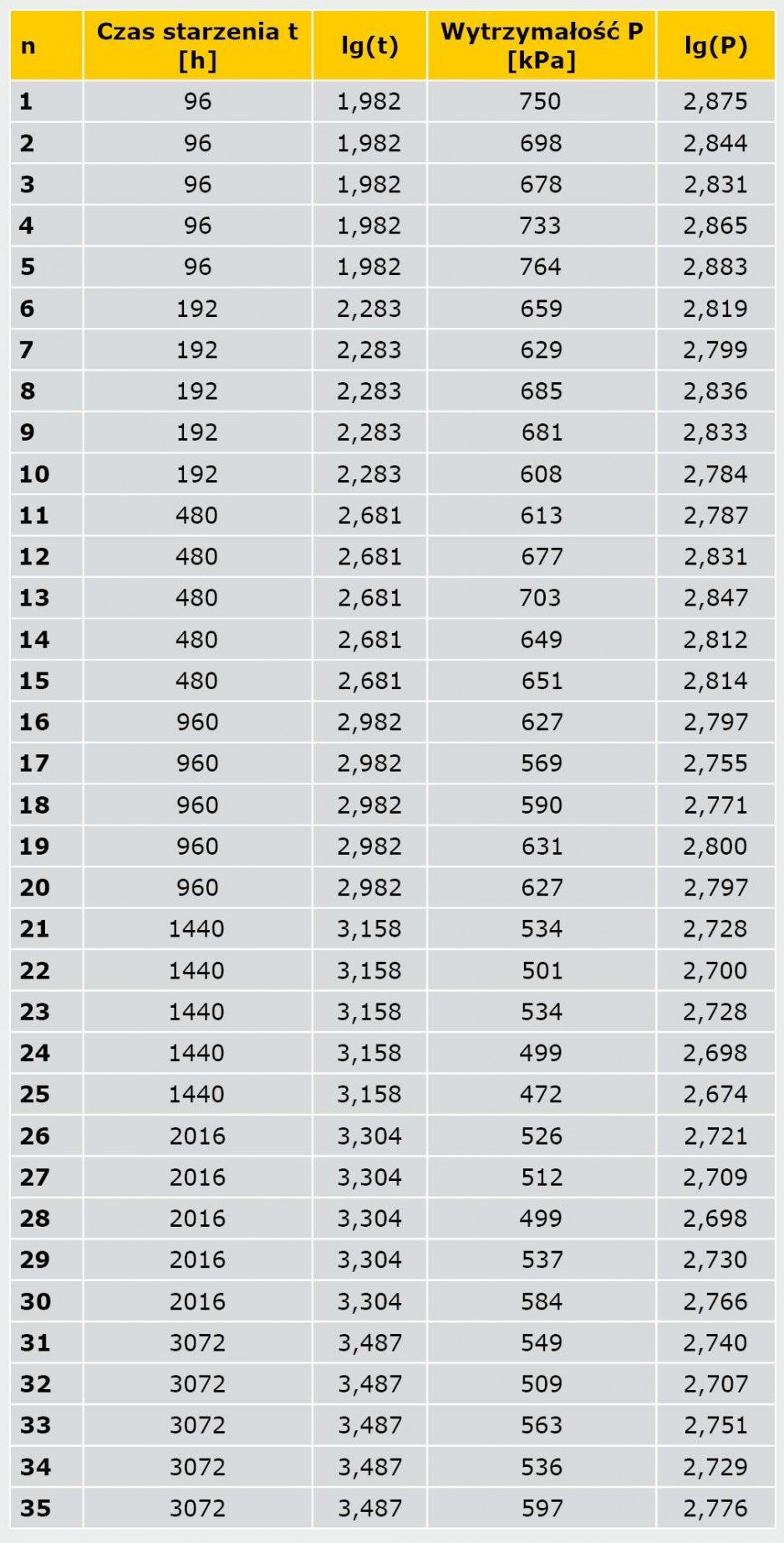
Wszystkie wyniki odniesiono do minimalnej założonej wartości po 10 latach, tj. 200 kPa. W TABELI 1 przedstawiono wyniki wytrzymałości na rozrywanie po starzeniu.
Analiza regresji
Należy znaleźć równanie, aby dopasować prostą wyrażoną równaniem:
y = a + bx (1)
gdzie:
y – logarytm z wytrzymałości na rozrywanie w kPa, lg(P),
a – punkt przecięcia prostej z osią współrzędnych na osi y,
b – współczynnik kierunkowy,
x – logarytm czasu w godzinach, lg(t).
Do analizy danych wyliczono następujące zmienne:
gdzie:
Sy – suma iloczynów reszt rezydualnych równoległych do osi y,
Sx – suma iloczynów reszt rezydualnych równoległych do osi x,
Sxy – suma iloczynów reszt rezydualnych prostopadłych do linii,
Y – średnia arytmetyczna danych y,
X – średnia arytmetyczna danych x,
n – całkowita liczba wyników (par dla xi, yi).
Następnie wyznaczono współczynnik korelacji liniowej r według równań:
Z odpowiednich tablic normy EN-705:1994 [2] potwierdzono przydatność danych do analizy (dla n = 35 wartość r większa niż 0,5541 – wymaganie spełnione).
Następnie obliczono a oraz b do równania (1) z wykorzystaniem równań:
W celu wykonania ekstrapolacji sprawdzono przydatność danych – obliczono M według równania:
gdzie:
tv – odnośna wartość dla rozkładu t studenta (dla n = 35 wynosząca 2,0345); wartość krytyczna testu dwustronnego (2,5% wartość górna, 5% wartość dwustronna poziomu ufności; tv dla 97,5%) [1, 2].
Następnie potwierdzono przydatność danych do ekstrapolacji (wartość M większa od zera – wymaganie spełnione) i przystąpiono do wyprowadzenia wartości długotrwałych. Jako minimalną wartość długotrwałości po 10 latach (P10,s,min) określono wartość 200 kPa, a współczynnik bezpieczeństwa Fs przyjęto jako 1,25. Obliczono minimalną długotrwałą wartość wytrzymałości (P10,min) według wzoru:
Z równania (1) po podstawieniu odpowiednich x obliczono ekstrapolowaną wartość wytrzymałości krótkotrwałej po 10 godz. (P10h) oraz ekstrapolowaną wartość wytrzymałości długotrwałej po 10 latach (P10), a następnie obliczono stosunek regresji RR:
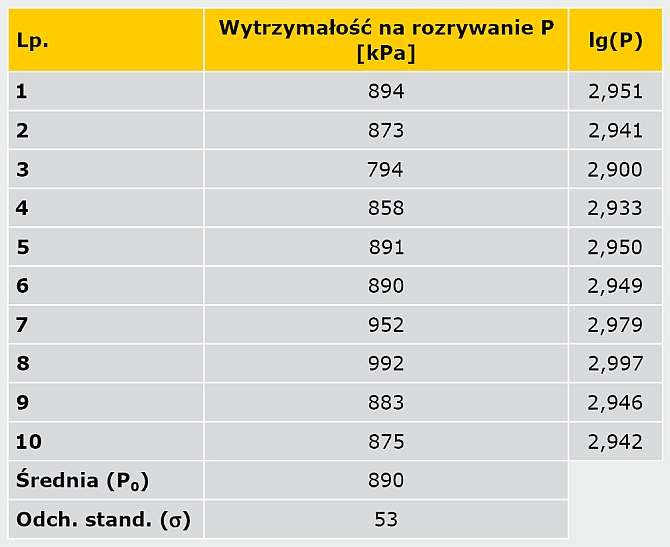
Na podstawie początkowych wyników wytrzymałości ( TABELA 2 ) obliczono współczynnik C, który ustala stosunek średniego wyniku badania wytrzymałości w próbach początkowych przeprowadzonych na systemie do ekstrapolowanej wartości 10 godz., na podstawie równania:
gdzie:
P0 - średnia z początkowych wartości wytrzymałości, czyli próbek niepoddanych starzeniu.
Następnie wyprowadzono minimalną wartość wytrzymałości początkowej P0,min:
Wyprowadzono wartość obliczeniową wytrzymałości początkowej P0,d:
gdzie:
s - odchylenie standardowe dla początkowych wyników badań wytrzymałości na rozrywanie.
Kolejno przystąpiono do określenia krótkotrwałej (P10h,d) oraz długotrwałej (P10,d) obliczeniowej wartości wytrzymałości, z wykorzystaniem równań:
Określono równanie prostej obliczeniowej według równania:
gdzie:
Pt,d - projektowa wartość wytrzymałości w danym czasie t,
b - nachylenie minimalnej i obliczeniowej linii regresji liniowej,
ad - stała obliczeniowej linii regresji, obliczona według równania (19):
gdzie:
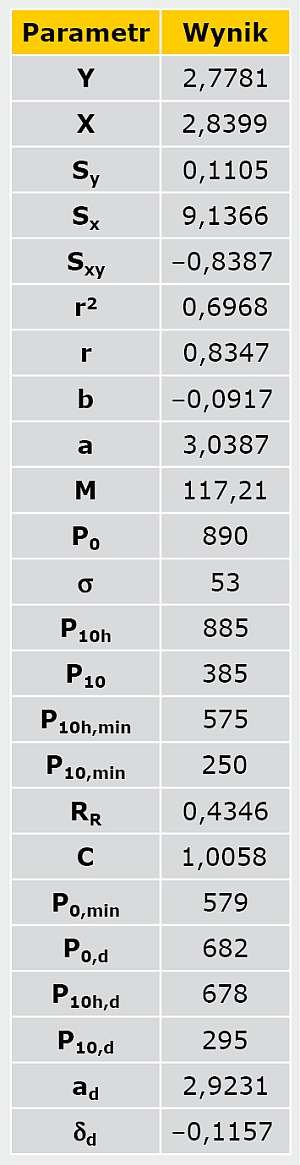
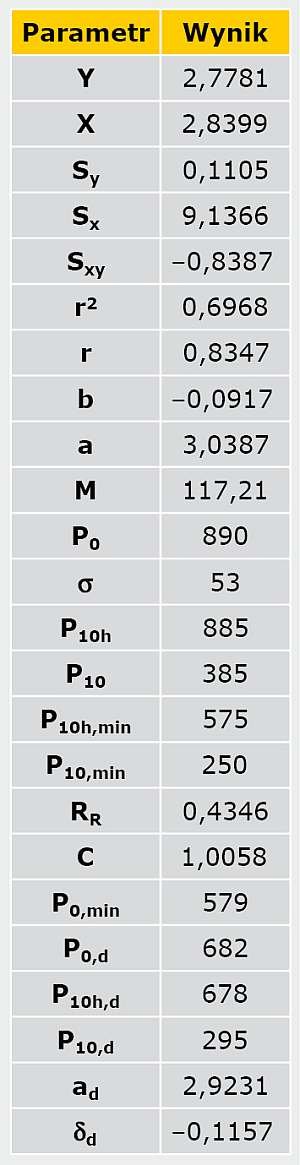
W TABELI 3 przedstawiono wyniki obliczeń.
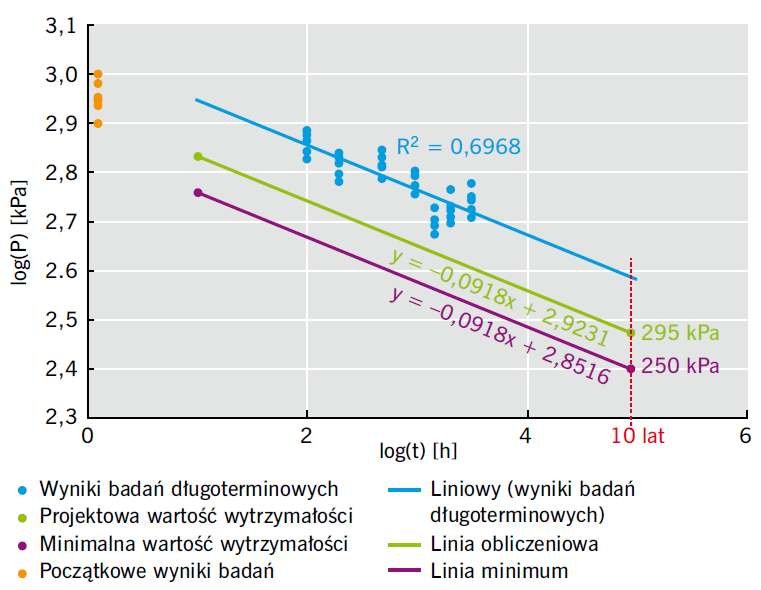
Na RYS. przedstawiono zmianę wytrzymałości w funkcji czasu oraz wszystkie wyniki badań wraz z obliczeniami. Wartość obliczeniowa wytrzymałości na rozrywanie po 10 latach użytkowania wynosi 295 kPa i przewyższa wymaganie minimalne z dodatkowym 25% współczynnikiem bezpieczeństwa, czyli 250 kPa.
Wyniki przeprowadzonych badań potwierdzają trwałość systemu na okres minimum 10 lat, co po uwzględnieniu innych istotnych parametrów oraz dodatkowych kryteriów może być podstawą do udzielenia gwarancji na okres 10 lat.
Podsumowanie
Przedstawiona na omówionym przykładzie analiza regresji z ekstrapolacją danych jest uniwersalnym narzędziem, służącym do przewidywania okresu trwałości lub zmiany parametru na bazie danych z badań starzeniowych oraz wytrzymałości początkowych.
Podobne metody stosowane są z powodzeniem od lat w innych gałęziach przemysłu i są pomocne nie tylko podczas projektowania produktu, lecz także w laboratoriach kontroli jakości.
W sektorze bezspoinowych systemów ociepleń, jak i w całej branży chemii budowlanej jest to nowatorskie, a zarazem odpowiedzialne podejście do wprowadzania produktu na rynek oraz udzielania gwarancji na kompletny system ociepleń.
Opracowanie i wdrożenie podobnych metod przez producentów chemii budowlanej wymaga od nich odpowiedniego sprzętu oraz chęci poniesienia odpowiedzialności za oferowane rozwiązania systemowe. Dzięki temu potencjalny użytkownik wyrobu budowlanego może uzyskać rzetelną informację, z jakim produktem ma do czynienia i na jaki minimalny termin szacuje się trwałość zastosowanego systemu.
Literatura
1. ASTM D3681-96, "Standard Test Method for Chemical Resistance of Fiberglass (Glass-Fiber-Reinforced Thermosetting-Resin) Pipe in a Deflected Condition", ANNEX - A1 "Least squares calculation for long term".
2. EN-705:1994, "Plastics piping systems. Glass reinforced thermosetting plastics (GRP) pipes an d fittings. Methods for regression analyses and their use".
3. ETAG 004, "Guideline for European Technical Approval of External Thermal Insulation Composite Systems with Rendering", Edition March 2000, Amendment June 2008.
4. ZUAT-15/V.03/2010, "Zestawy wyrobów do wykonywania ociepleń ścian zewnętrznych z zastosowaniem styropianu jako materiału termoizolacyjnego i pocienionej wyprawy elewacyjnej (ETICS)", Wydanie III, Warszawa 2010.
5. W. Ligęza, :O problemach technicznej oceny jakości wykonania ociepleń metodą bezspoinową", "Czasopismo Techniczne", z. 1-B/2007, Kraków 2007.
6. G. Wypych, "Handbook of Material Weathering", ChemTec Publishing, Toronto‑Scarborough 1995.