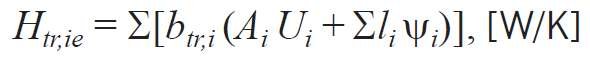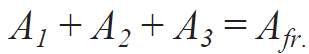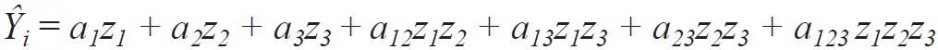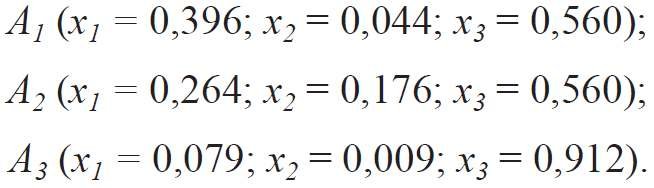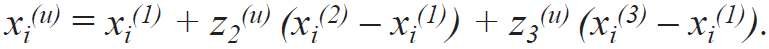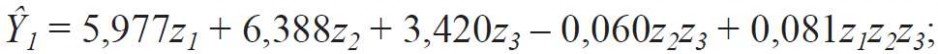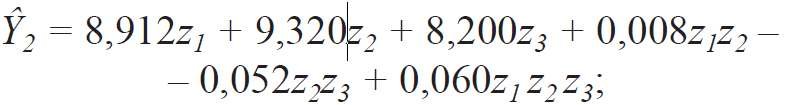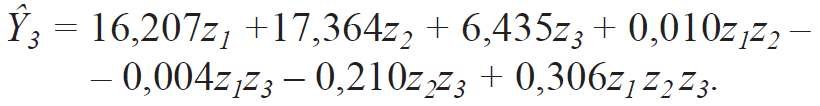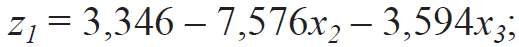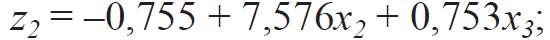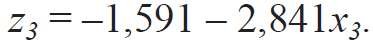Analiza współczynnika przenoszenia ciepła fragmentu ściany zewnętrznej z oknem
Analysis of heat transfer coefficient for an external wall fragment with a window

Dzięki coraz lepszym technologiom projektowania, wyrobu i montażu stolarki okiennej producenci mogą proponować konsumentom okna o niestandardowych rozmiarach i kształtach o bardzo dobrych właściwościach termoizolacyjnych.
www.pixabay.com
Zgodnie z wciąż rosnącymi wymaganiami ochrony cieplnej budynków Warunki Techniczne, jakim powinny odpowiadać budynki i ich usytuowanie, podają, że maksymalny dopuszczany współczynnik przenikania ciepła okien w budynkach mieszkalnych na chwilę obecną (do 2021 r.) wynosi 1,1 W/(m2·K), zaś maksymalny dopuszczalny współczynnik przenikania ciepła ścian zewnętrznych w budynkach mieszkalnych - 0,23 W/(m2·K) [1]. Jednakże należy pamiętać, że te wymagania dotyczą budynków nowo wznoszonych.
Zobacz także
M.B. Market Ltd. Sp. z o.o. Czy piana poliuretanowa jest palna?

W artykule chcielibyśmy przyjrzeć się bliżej temu aspektowi i rozwiać wszelkie wątpliwości na temat palności pian poliuretanowych.
W artykule chcielibyśmy przyjrzeć się bliżej temu aspektowi i rozwiać wszelkie wątpliwości na temat palności pian poliuretanowych.
Ultrapur Sp. z o.o. Pianka poliuretanowa a szczelność budynku

Wielu inwestorów, wybierając materiał do ocieplenia domu, kieruje się głównie parametrem lambda, czyli wartością współczynnika przewodzenia ciepła. Jest on jedynym zestandaryzowanym współczynnikiem, który...
Wielu inwestorów, wybierając materiał do ocieplenia domu, kieruje się głównie parametrem lambda, czyli wartością współczynnika przewodzenia ciepła. Jest on jedynym zestandaryzowanym współczynnikiem, który określa właściwości izolacyjne materiału. Jednocześnie jest współczynnikiem wysoce niedoskonałym – określa, jak dany materiał może opierać się utracie ciepła poprzez przewodzenie.
Rockwool Polska Termomodernizacja domu – na czym polega i jak ją zaplanować?

Termomodernizacja to szereg działań mających na celu poprawę energochłonności Twojego domu. Niezależnie od zakresu inwestycji, kluczowa dla osiągnięcia spodziewanych efektów jest kolejność prac. Najpierw...
Termomodernizacja to szereg działań mających na celu poprawę energochłonności Twojego domu. Niezależnie od zakresu inwestycji, kluczowa dla osiągnięcia spodziewanych efektów jest kolejność prac. Najpierw należy docieplić ściany i dach, aby ograniczyć zużycie energii, a dopiero potem zmodernizować system grzewczy. Dzięki kompleksowej termomodernizacji domu prawidłowo wykonanej znacznie zmniejszysz koszty utrzymania budynku.
Budynki, które już istnieją, charakteryzują się bardzo zróżnicowanymi właściwościami cieplnymi zarówno ścian, jak i stolarki okiennej. W takich wypadkach bardzo często podejmowanym przedsięwzięciem termomodernizacyjnym jest wymiana okien starych, nierzadko nieszczelnych i zimnych, na nowe, o bardzo dobrych parametrach cieplnych.
Przy montażu stolarki okiennej nie można zapomnieć o nowoczesnych metodach osadzania okien w ścianach osłonowych, dzięki którym następuje praktycznie całkowita eliminacja negatywnego wpływu liniowych mostków cieplnych na styku rama–ściana. Dzięki udoskonalaniu technologii projektowania, wyrobu i montażu stolarki okiennej producenci są w stanie proponować konsumentom okna o niestandardowych rozmiarach i kształtach, które nie tracą swych bardzo dobrych właściwości termoizolacyjnych.
Niezwykle często projektanci są postawieni przed problemem odpowiedniego doboru wymiarów stolarki okiennej do już istniejących ścian osłonowych o bardzo dobrych bądź wyjątkowo złych właściwościach cieplnych. W takiej sytuacji istnieje potrzeba doboru odpowiedniej strategii, której celem jest zapewnienie optymalnie wysokich właściwości cieplnych kompleksowej przegrody zewnętrznej (ściany z oknem) z doborem właściwych parametrów cieplnych i pól powierzchni poszczególnych elementów tworzących analizowaną przegrodę.
W związku z tą sytuacją celem przedstawionego badania jest analiza wpływu udziałów powierzchni elementów składowych (ściany, ramy i powierzchni szklonej) oraz parametrów fizykalnych charakteryzujących przenikanie ciepła w tych elementach (współczynników przenikania ciepła ściany, ramy i oszklenia) na współczynnik przenoszenia ciepła przez przenikanie ze strefy ogrzewanej do środowiska zewnętrznego fragmentu ściany zewnętrznej z oknem w budynku mieszkalnym, z opracowaniem deterministycznych modeli matematycznych zależności oraz określeniem wartości optymalnych badanych czynników.
Opis obiektu
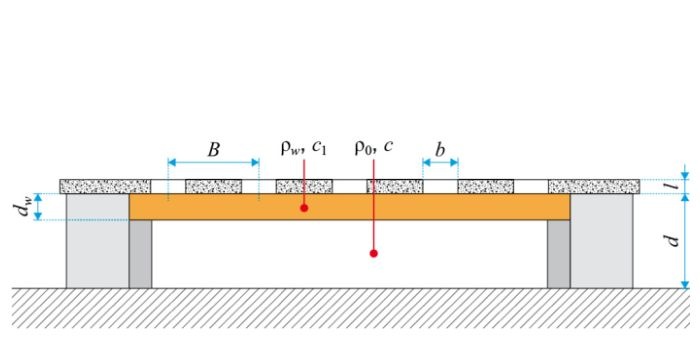
Przegroda zewnętrzna każdego pomieszczenia mieszkalnego w budynkach mieszkalnych najczęściej jest fragmentem składającym się ze ściany i okna. Z uwzględnieniem nowych technologii montażu okien, dopuszczających szerokie możliwości zastosowania różnych rozwiązań ramy i różnorodnych typów oszklenia, z bardzo zróżnicowanymi cechami fizykalnymi zarówno w odniesieniu do ściany osłonowej, jak i samego okna, jako obiekt badania dla dalszej analizy przyjęto fragment ściany z trzema elementami: ścianą, ramą okienną i powierzchnią szkloną. Schematy takiego fragmentu pokazano na rys. 1.
Rozmiary fragmentu przegrody zewnętrznej uwzględniają rozwiązania przestrzenne pomieszczeń mieszkalnych i przyjęte zostały następująco:
2,80×3,60 m = 10,08 m2.
W ramach tej wartości w badaniu zmieniały się różne kombinacje pól powierzchni okien, od rozmiaru 0,60×1,48 m = 0,888 m2 do 3,00×1,48 m = 4,440 m2.
Wysokość okna w analizowanym przypadku należało przyjąć jako wartość stałą, gdyż w oknach referencyjnych w budynkach mieszkalnych wynosi ona 1,48 m [2].
Powód przyjęcia wysokości okna jako parametru stałego w badaniu został wyjaśniony w dalszej części pracy.
Metoda obliczania współczynnika przenoszenia ciepła
Współczynnik przenoszenia ciepła przez przenikanie ze strefy ogrzewanej do środowiska zewnętrznego w przegrodach budowlanych jest jedną z najważniejszych wielkości przy obliczeniach zapotrzebowania ciepła na energię użytkową w budynkach ogrzewanych. Charakteryzuje on przenoszenie ciepła nie przez 1 m2 (jak współczynnik przenikania ciepła U), lecz przez pewny fragment przegrody z polem powierzchni Afr, zawierający kilka elementów składowych.
Oblicza się ten współczynnik wg wzoru [3]:
![]() (1)
(1)
gdzie:
btr,i - współczynnik redukcyjny obliczeniowej różnicy temperatur (przyjęto btr,i = 1);
Ai - pole powierzchni i-tej przegrody, [m2];
Ui - współczynnik przenikania ciepła i-tej przegrody, [W/(m2·K)];
li - długość liniowego mostka cieplnego, [m];
yi - liniowy współczynnik przenikania ciepła mostka liniowego, [W/(m·K)].

RYS. 2. Schemat blokowy obliczania współczynnika przenoszenia ciepła: Htr; hw - wysokość okna; Aw = A1 + A2 - powierzchnia okna; bw - szerokość okna; C - udział powierzchni szklonej do powierzchni okna, bf - szerokość elementów ramy; rys. autorów (W. Jezierski, J. Borowska)
Mimo prostego wyrazu, wzór (1) jest bardzo złożoną zależnością dla przeprowadzenia analizy czynnikowej. Nawet przy trzech elementach składowych wzór ten daje aż 10 czynników do przeanalizowania. Są to
A1, A2, A3 - pola powierzchni odpowiednio oszklenia, ramy i ściany;
U1, U2, U3 - współczynniki przenikania ciepła odpowiednio oszklenia, ramy i ściany;
l1, l2 - długości liniowe mostków cieplnych odpowiednio na styku szkło–rama i styku rama–ściana;
ψ1, ψ2 - liniowe współczynniki przenikania ciepła mostka liniowego odpowiednio na styku szkło–rama i styku rama–ściana.
Każdy dodatkowy element składowy zwiększa liczbę czynników o 4 lub 6 parametrów.
Jednak najtrudniejszym zadaniem dla przeprowadzenia analizy był warunek, którym są powiązane trzy pierwsze zmienne:
![]() (2)
(2)
Do wykonania obliczeń Htr,ie, zaplanowanych w eksperymencie obliczeniowym, autorzy stworzyli specjalny algorytm (rys. 2). Ten algorytm posłużył jako podstawa do opracowania autorskiego programu w Microsoft Excel.
Model matematyczny do określenia współczynnika przenoszenia ciepła przez przenikanie
Wstępna analiza czynników pozwoliła wykryć, że oprócz zmiennych A1, A2, A3 oraz l1 i l2, pozostałe zmienne są sterowalne, mierzalne, wzajemnie niezależne, niesprzeczne i odpowiadają podstawowym wymaganiom modelowania matematycznego [4].
Zmienne l1 i l2 są zależne od A1 i A2 oraz niejednoznaczne. W celu zapewnienia jednoznaczności l1 i l2 wysokość okna przyjęto jako wartość stałą.
Zgodnie z przyjętym celem badania, współczynnik przenoszenia ciepła Htr (funkcja celu Y) postanowiono zbadać w zależności od trzech czynników geometrycznych:
- udziałów powierzchni szklonej (czynnik z1),
- powierzchni ramy (czynnik z2),
- powierzchni ściany (czynnik z3)
przy uwzględnieniu wpływu trzech czynników fizykalnych - współczynników przenikania ciepła:
- oszklenia U1,
- ramy U2,
- ściany U3.
Pozostałe parametry przyjęto na stałym poziomie.
Ponieważ czynniki geometryczne z1, z2, z3 są związane warunkiem (2), to do zbadania ich wpływu zastosowano planowanie sympleksowe dla trzech zmiennych w układzie „skład–własność” zawierającego N = 7 prób (tabela 1) [5].
Planowanie sympleksowe tradycyjnie stosuje się do opracowania modeli matematycznych zależności właściwości dowolnych mieszanek od udziału składników. Dzięki wykrytemu podobieństwu formalnemu autorzy zastosowali to podejście do rozwiązania zagadnienia z fizyki budowli.
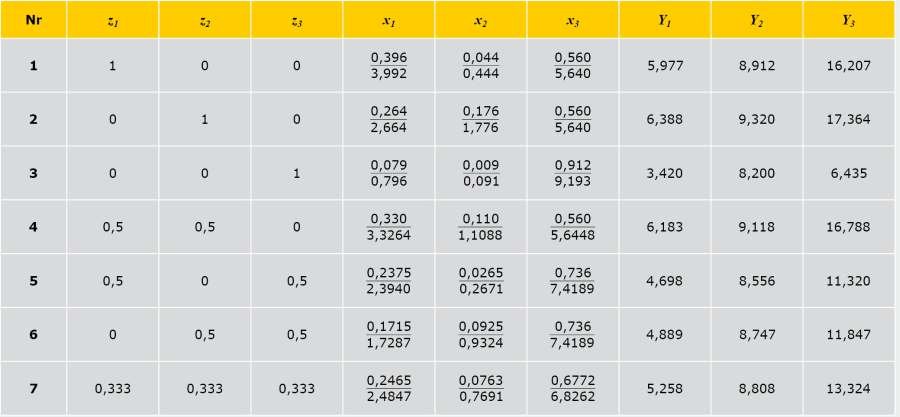
TABELA 1. Plan eksperymentu, gdzie z1, z2, z3 – czynniki geometryczne; χ1, χ2, χ3 – poziomy zmienności rozpatrywanych czynników (w liczniku – udziały; w mianowniku – powierzchnie, m2); Y1, Y2, Y3 – wyniki obliczeń współczynnika przenoszenia ciepła przez przenikanie
Ten plan przewiduje określony układ realizacji obliczeń przy spełnieniu warunku z1 + z2 + z3 = 1 i opracowanie modelu w postaci niepełnego wielomianu trzeciego stopnia dla trzech zmiennych:
![]() (3)
(3)
Wpływ niezależnych czynników fizykalnych U1, U2, U3 może być uwzględniony poprzez realizację w każdym z siedmiu punktów planu sympleksowego dla Y = f(z1, z2, z3) dodatkowo tradycyjnego planu trójczynnikowego dla Y = ƒ(U1, U2, U3).
Po odpowiedniej obróbce wyników mielibyśmy model zależności Y od sześciu czynników, jednak postać tego modelu byłaby bardzo skomplikowana.
Dążąc do uproszczenia modelu oraz osiągnięcia celu badania, podjęto decyzję o opracowaniu modeli w postaci Yi= ƒ(z1, z2, z3) dla każdego z trzech następujących układów parametrów fizykalnych:
- model Y1 – „dobre okno”:
U1= 0,70 W/(m2·K); U2= 1,10 W/(m2·K); ψ1 = ψ2= 0,08 W/(m·K)
+ „dobra ściana”: U3= 0,23 W/(m2·K); - model Y2 – „dobre okno”:
U1= 0,70 W/(m2·K); U2= 1,10 W/(m2·K); ψ1 = ψ2 = 0,08 W/(m·K)
+ „zła ściana”: U3= 0,75 W/(m2·K); - model Y3 – „złe okno”:
U1= 2,10 W/(m2·K); U2= 3,30 W/(m2·K); ψ1 = ψ2 = 0,29 W/(m·K)
+ „dobra ściana”: U3= 0,23 W/(m2·K).
Według planu (tabela 1) każdy z czynników z1, z2, z3 należy rozpatrywać na czterech poziomach:
- 0;000;
- 0,333;
- 0,500;
- 1,000.
Ten warunek nie odpowiadał przyjętemu celowi, ponieważ nie miało sensu wykonywać badania w całym zakresie zmiany udziałów wybranych czynników (od 0 do 1).
Praktyczne znaczenie miały jedynie takie zakresy zmienności czynników, które odpowiadały realnym układam fragmentu ściany z oknem.
W związku z tym w badaniu zastosowano lokalne planowanie sympleksowe w warunkach ograniczenia zakresu zmienności wszystkich czynników [6]. Procedura realizacji tego podejścia została szczegółowo opisana w innych pracach autorów [7-8].
Na podstawie wstępnej analizy wybranego fragmentu ściany został wybrany podobszar obejmujący preferowane udziały elementów składowych: powierzchni szklonej (χ1) - od 0,079 do 0,396; ramy (χ2) - od 0,009 do 0,176; ściany (χ3) - od 0,560 do 0,912.
Wartości udziałów składników określały współrzędne wierzchołków wybranego do badania podobszaru:

Wyżej wymieniony podobszar został transformowany do pełnego planu sympleksowego poprzez wprowadzenie pseudoskładników z1, z2, z3, które w każdym u-tym układzie planu są związane z czynnikami rzeczywistymi χ1, χ2, χ3 zależnością [6]:
![]() (4)
(4)
Poziomy zmienności czynników z1, z2, z3 oraz odpowiadające im rzeczywiste czynniki χ1, χ2, χ3 przedstawiono w tabeli 1.
Po przeprowadzeniu niezbędnych obliczeń możliwe było opracowanie modeli badanych cech w zależności od pseudoskładników (z1, z2, z3).
Chcąc otrzymać modele matematyczne z czynnikami w postaci naturalnej (x1, x2, x3), należało odkodować je przez podstawienie odpowiednich zależności.
Za pomocą wzorów, podanych w [5] opracowano zależności Yi = ƒ(z1, z2, z3):
- dla układu „dobre okno” + „dobra ściana”:
![]() (5)
(5)
- dla układu „dobre okno” + „zła ściana”:
 (6)
(6)
- dla układu „złe okno” + „dobra ściana”:
 (7)
(7)
Po sprawdzeniu adekwatności opracowanych modeli wg [5] (procedura ta została szczegółowo opisana przez autorów w [7]) uznano ich przydatność do dalszej analizy. Jednak najpierw otrzymano formuły związku pomiędzy współrzędnymi naturalnymi χi i systemem współrzędnych zi:
![]() (8)
(8)
![]() (9)
(9)
![]() (10)
(10)
Analiza wyników badania
Do interpretacji wyników badania zastosowano modele (5), (6) i (7), na podstawie których opracowano wykresy w postaci izolinii badanych zależności od rozpatrywanych czynników we współrzędnych pseudoskładników z1, z2, z3 (RYS. 3, RYS. 4 i RYS. 5) dla każdego z układów fragmentu ściany.
Te modele pozwoliły powiększyć badany podobszar do pełnych trójkątów sympleksowych, znacznie ułatwiając interpretację wyników. Natomiast merytoryczną interpretację wykonano na podstawie TAB. 1 przy zastosowaniu naturalnych współrzędnych χ1, χ2, χ3.
Jak widać z RYS. 3,:
- najwyższą wartość (6,388 W/K) współczynnika przenoszenia ciepła Y1 fragmentu dla układu „dobre okno” + „dobra ściana” uzyskano w wierzchołku Z2 (punkt 2) przy χ1 = 0,264; χ2 = 0,176; χ3 = 0,560 (TAB. 1),
- natomiast najniższą (3,420 W/K) w wierzchołku Z3 (punkt 3) przy χ1 = 0,079; χ2 = 0,009; χ3 = 0,912.
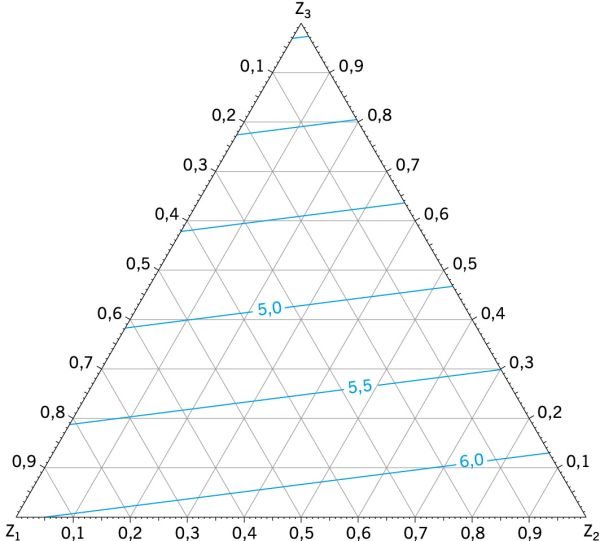
RYS. 3. Zależność współczynnika przenoszenia ciepła Y1 fragmentu ściany z oknem dla układu "dobre okno" [U1 = 0,70 W/(m2·K); U2 = 1,10 W/(m2·K); ψ1 = ψ2 = 0,08 W/(m·K)] + "dobra ściana" [U3 = 0,23 W/(m2·K)], od udziałów elementów składowych z1 - powierzchnia oszklenia, z2 - powierzchnia ramy, z3 - powierzchnia ściany rys. autorów (W. Jezierski, J. Borowska)
W sensie praktycznym oznacza to, że w badanym fragmencie ściany zamiana okna o powierzchni Ao3 = 1,48×0,60 = 0,887 m2 z udziałem powierzchni szklonej do powierzchni okna C = 0,90 (co odpowiada parametrom dla punktu 2) na okno o powierzchni Ao2= 1,48×2,993 = 4,43 m2 z udziałem powierzchni szklonej C = 0,60 (co odpowiada parametrom dla punktu 2) spowoduje wzrost współczynnika przenoszenia ciepła Y1 fragmentu ściany z układem „dobre okno” + „dobra ściana” o 86,8%.
Zastosowanie w tym samym fragmencie standardowego okna o powierzchni Aos = 1,48×1,23 = 1,820 m2 z udziałem powierzchni szklonej C = 0,70 i szerokości elementów ramy bf= 0,11 m daje wartość współczynnika przenoszenia ciepła fragmentu Y1= 4,189 W/K.
Z RYS. 4 wynika, że najwyższą wartość (9,320 W/K) współczynnika przenoszenia ciepła Y2 fragmentu dla układu „dobre okno” + „zła ściana” uzyskano także w wierzchołku Z2 (punkt 2) przy χ1 = 0,264; χ2 = 0,176; χ3 = 0,560 (TAB. 1), natomiast najniższą (8,200 W/K) też w wierzchołku Z3 (punkt 3) przy χ1 = 0,079; χ2 = 0,009; χ3 = 0,912. Poziom średni Y2 mocno wzrósł w porównaniu z Y1, natomiast rola okna przy „złej” ścianie jest inna.
Wahania pól powierzchni oszklenia i ramy dają znacznie słabsze efekty w podwyższeniu Y2. Tak przy zamianie w badanym fragmencie ściany okna o powierzchni Ao3= 1,48×0,60 = 0,887 m2 z udziałem powierzchni szklonej do powierzchni okna C = 0,90 (co odpowiada parametrom dla punktu 3) na okno o powierzchni Ao2= 1,48×2,993 = 4,43 m2 z udziałem powierzchni szklonej C = 0,60 (co odpowiada parametrom dla punktu 2) wzrost współczynnika przenoszenia ciepła Y2 fragmentu ściany z układem „dobre okno” + „zła ściana” wynosi tylko 13,7%.
![RYS. 4. Zależność współczynnika przenoszenia ciepła Y2 fragmentu ściany z oknem dla układu „dobre okno” [U1 = 0,70 W/(m2· K); U2= 1,10 W/(m2 · K); ψ1 = ψ2 = 0,08 W/(m · K)] + „zła ściana”[U3 = 0,75 W/(m2 · K)], od udziałów elementów składowych; rys.: archiwum autorów (W. Jezierski, J. Borowska) RYS. 4. Zależność współczynnika przenoszenia ciepła Y2 fragmentu ściany z oknem dla układu „dobre okno” [U1 = 0,70 W/(m2· K); U2= 1,10 W/(m2 · K); ψ1 = ψ2 = 0,08 W/(m · K)] + „zła ściana”[U3 = 0,75 W/(m2 · K)], od udziałów elementów składowych; rys.: archiwum autorów (W. Jezierski, J. Borowska)](https://www.izolacje.com.pl/media/cache/typical_view/data/202102/b-rysunek4.jpg)
RYS. 4. Zależność współczynnika przenoszenia ciepła Y2 fragmentu ściany z oknem dla układu „dobre okno” [U1 = 0,70 W/(m2· K); U2= 1,10 W/(m2 · K); ψ1 = ψ2 = 0,08 W/(m · K)] + „zła ściana” [U3 = 0,75 W/(m2 · K)], od udziałów elementów składowych; rys.: archiwum autorów (W. Jezierski, J. Borowska)
Zastosowanie w tym samym fragmencie standardowego okna dobrej jakości o powierzchni Ao1= 1,48×1,23 = 1,820 m2 z udziałem powierzchni szklonej C = 0,70 i szerokości elementów ramy bf= 0,11 m dało wartość współczynnika przenoszenia ciepła fragmentu Y2= 8,484 W/K.
Porównując tę wartości z wartością Y1, także uzyskaną przy zastosowaniu okna standardowego, można stwierdzić, że zła jakość ściany spowodowała wzrost współczynnika przenoszenia ciepła z 4,189 do 8,484 W/K, tj. o 102,5%.
Najwyższą wartość (17,364 W/K) współczynnika przenoszenia ciepła Y3 fragmentu dla układu "złe okno" + "dobra ściana" uzyskano także w wierzchołku z2 (punkt 2) (rys. 5) przy x1 = 0,264; x2 = 0,176; x3 = 0,560 (tabela 1), natomiast najniższą (6,435 W/K) w tym samym wierzchołku Z3 (punkt 3) przy x1 = 0,079; x2 = 0,009; x3 = 0,912.
Rola okna przy jego "złej" jakości jest bardzo istotna. To wyraźnie widać przy ocenie wpływu pól powierzchni oszklenia i ramy na podwyższenie Y3. Tak przy zamianie w badanym fragmencie ściany okna o powierzchni Ao3 = 1,48×0,60 = 0,887 m2 z udziałem powierzchni szklonej do powierzchni okna C = 0,90 (co odpowiada parametrom dla punktu 3) na okno o powierzchni Ao2 = 1,48×2,993 = 4,43 m2 z udziałem powierzchni szklonej C = 0,60 (co odpowiada parametrom dla punktu 2) wzrost współczynnika przenoszenia ciepła Y3 fragmentu ściany z układem "złe okno" + "dobra ściana" wynosi aż 169,8%.
Zastosowanie w tym samym fragmencie standardowego okna złej jakości o powierzchni Ao1 = 1,48×1,23 = 1,820 m2 z udziałem powierzchni szklonej C = 0,70 i szerokości elementów ramy bf = 0,11 m daje wartość współczynnika przenoszenia ciepła Y1 = 9,264 W/K. Porównując tę wartość z wartością Y1, uzyskaną przy zastosowaniu okna standardowego wysokiej jakości, można stwierdzić, że zła jakość okna spowodowała wzrost współczynnika przenoszenia ciepła fragmentu z 4,189 do 9,264 W/K, tj. o 121,2%.
![RYS. 5. Zależność współczynnika przenoszenia ciepła Y3 fragmentu ściany z oknem dla układu „złe okno” [U1 = 2,10 W/(m2 · K); U2 = 3,30 W/(m2 · K); ψ1 = ψ2 = 0,29 W/(m · K)] + „dobra ściana” [U3 = 0,23 W/(m2 · K)], od udziałów elementów składowych; rys.: archiwum autorów (W. Jezierski, J. Borowska) RYS. 5. Zależność współczynnika przenoszenia ciepła Y3 fragmentu ściany z oknem dla układu „złe okno” [U1 = 2,10 W/(m2 · K); U2 = 3,30 W/(m2 · K); ψ1 = ψ2 = 0,29 W/(m · K)] + „dobra ściana” [U3 = 0,23 W/(m2 · K)], od udziałów elementów składowych; rys.: archiwum autorów (W. Jezierski, J. Borowska)](https://www.izolacje.com.pl/media/cache/typical_view/data/202102/b-rysunek5.jpg)
RYS. 5. Zależność współczynnika przenoszenia ciepła Y3 fragmentu ściany z oknem dla układu „złe okno” [U1 = 2,10 W/(m2 · K); U2 = 3,30 W/(m2 · K); ψ1 = ψ2 = 0,29 W/(m · K)] + „dobra ściana” [U3 = 0,23 W/(m2 · K)], od udziałów elementów składowych; rys.: archiwum autorów (W. Jezierski, J. Borowska)
Wnioski
Za pomocą opracowanych modeli matematycznych oszacowano efekty wpływu udziałów pól powierzchni oszklenia, ramy i ściany oraz ich parametrów cieplnych na współczynnik przenoszenia ciepła fragmentu ściany z oknem w budynku mieszkalnym.
W przyjętym zakresie zmienności wahania pól powierzchni oszklenia i ramy mogą spowodować wzrost współczynnika przenoszenia ciepła fragmentu ściany z oknem o 86,8%.
W wypadku ściany niespełniającej obecnych wymagań ochrony cieplnej efekt wpływu wahań pól powierzchni oszklenia i ramy słabnie do kilkunastu procent. Główna rola w prawie dwukrotnym podwyższeniu współczynnika przenoszenia ciepła fragmentu należy do ściany.
Najgorszym rozwiązaniem fragmentu przegrody zewnętrznej okazał się wariant z wykorzystaniem okien o niskiej termoizolacji. Wzrost wpływu wahań pól powierzchni oszklenia i ramy na współczynnik przenoszenia ciepła osiąga wtedy 169,8%. Potwierdza to celowość wymiany okien w pierwszej kolejności przy częściowej termomodernizacji budynków.
Literatura
- Rozporządzenie Ministra Infrastruktury w sprawie warunków technicznych, jakim powinny odpowiadać budynki i ich usytuowanie, z dnia 17 lipca 2015 r.
- PN-EN 14351-1+A2:2016-10, „Okna i drzwi – Część 1: Okna i drzwi zewnętrzne bez właściwości dotyczących odporności ogniowej i/lub dymoszczelności”.
- Rozporządzenie Ministra Infrastruktury i Rozwoju z dnia 27 lutego 2015 r. w sprawie metodologii wyznaczania charakterystyki energetycznej budynku lub części budynku oraz świadectw charakterystyki energetycznej.
- J. Gutenbaum, „Modelowanie matematyczne systemów”. Wyd. EXIT, Warszawa 2003.
- V.Z. Brodskiy, L.I. Brodskiy, T.I. Golikova i in., „Tablicy planov eksperimenta dla faktornyh i polinomial’nyh modelej”, Metalurgiâ, Moskva 1982.
- I.G. Zedginidze, „Matematiczeskoje planirovanie eksperymenta dla issledovaniâ i optimizacii svoistv smesej”, Mecniereba, Tbilisi 1986.
- 7. W. Jezierski, J. Borowska, „Model matematyczny współczynnika przenikania ciepła ściany osłonowej z oknem z uwzględnieniem powierzchni elementów składowych”, „Izolacje” 1/2018, s. 50–54.






![RYS. 3. Zależność współczynnika przenoszenia ciepła Y<sub>1</sub> fragmentu ściany z oknem dla układu „dobre okno”[U<sub>1</sub> = 0,70 W/(m<sup>2</sup> · K)]; U<sub>2</sub> = 1,10 W/(m<sup>2</sup> · K);
ψ<sub>1</sub> = ψ<sub>2</sub> = 0,08 W/(m · K)] .](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/rysunek3-3.jpg)
![RYS. 4. Zależność współczynnika przenoszenia ciepła Y<sub>2</sub> fragmentu ściany z oknem dla układu „dobre okno” [U<sub>1</sub> = 0,70 W/(m<sup>2</sup>· K); U<sub>2</sub>= 1,10 W/(m2 · K); ψ<sub>1</sub> = ψ<sub>2</sub> = 0,08 W/(m · K)] + „zła ściana”[.](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/rysunek4-2.jpg)
![RYS. 5. Zależność współczynnika przenoszenia ciepła Y<sub>3</sub> fragmentu ściany z oknem dla układu „złe okno” [U<sub>1</sub> = 2,10 W/(m<sup>2</sup> · K); U<sub>2</sub> = 3,30 W/(m<sup>2</sup> · K);
ψ<sub>1</sub> = ψ<sub>2</sub> = 0,29 W/(m · K)] + „.](https://www.izolacje.com.pl/media/cache/typical_view/data/202101/rysunek5-1.jpg)